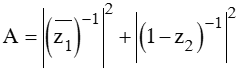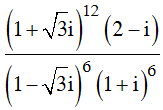Cho số phức z thỏa mãn |z +1 +i | =| z ngang- 2i|
Câu hỏi:
Cho số phức z thỏa mãn |z +1 +i | =| - 2i |. Tìm giá trị nhỏ nhất của |z|.
A.
B. 1
C.
D. 2
Trả lời:
Chọn C.
Gọi z = x+ yi thì M (x; y) là điểm biểu diễn z
Ta có |z +1 +i | =| - 2i |
Nên ( x + 1) 2 + (y + 1) 2 = x2 + (y + 2) 2 hay ∆: x – y – 1 = 0.
Do đó điểm M di chuyển trên ∆. Do đó; để modul của số phức z min khi M là hình chiếu của O trên ∆
Vậy 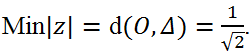
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho các số phức z thỏa mãn |z – 2 – 4i| = 2. Gọi z1; z2 số phức có module lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức bằng?
Xem lời giải »
Câu 2:
Gọi z1, z2 lần lượt là hai nghiệm của phương trình z2 - (1 + 3i) z – 2 + 2i = 0 và thỏa mãn | z1| > | z2|. Tìm giá trị của biểu thức
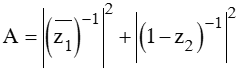
Xem lời giải »
Câu 3:
Gọi z1; z2 lần lượt là hai nghiệm của phương trình z2 – 4z + 7 = 0 .Tính giá trị của biểu thức 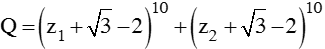
Xem lời giải »
Câu 4:
Cho các số phức z thỏa mãn |z2 + 4| = 2|z|. Kí hiệu M = max|z| và m = min|z|. Tìm module của số phức w = M + m?
Xem lời giải »
Câu 5:
Tính tổng
Xem lời giải »
Câu 6:
Cho số phức z thỏa mãn |z – 1 – 2i| = 2. Giá trị lớn nhất của T = |z| + |z – 3 – 6i| gần với giá trị nào nhất?
Xem lời giải »
Câu 7:
Cho số phức z thỏa mãn | z -3 - 4i| = .Tìm |z| để biểu thức: P = |z + 2|2 - |z – i|2 đạt giá trị lớn nhất?
Xem lời giải »
Câu 8:
Tìm mô-đun của số phức w = b + ci biết số phức 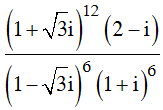 là nghiệm của phương trình z2 + 8bz + 64c = 0
là nghiệm của phương trình z2 + 8bz + 64c = 0
Xem lời giải »