Cho điểm A nằm ngoài đường tròn tâm O, từ A vẽ hai tiếp tuyến AB, AC; B và C là hai tiếp điểm và một cát tuyến ADE đến (O). a) Chứng minh AB2 = AD.AE.
Câu hỏi:
Cho điểm A nằm ngoài đường tròn tâm O, từ A vẽ hai tiếp tuyến AB, AC; B và C là hai tiếp điểm và một cát tuyến ADE đến (O).
a) Chứng minh AB2 = AD.AE.
b) Gọi H là giao điểm của OA và BC. Chứng minh tứ giác DEOH nội tiếp, chứng minh HB là tia phân giác của
Trả lời:
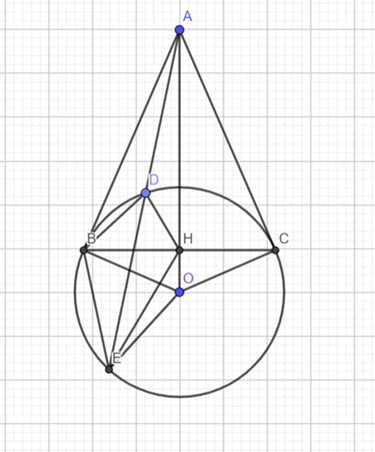
a) Xét tam giác ABD và tam giác ABE có:
Chung
(vì AB là tiếp tuyến (O))
⇒ ∆ABD ∽ ∆AEB (g.g)
⇒
⇒ AB2 = AD.DE
b) Ta có: AB,AC là tiếp tuyến của (O)
⇒AB ⊥ OB, BC ⊥ AO
⇒ BH ⊥ AO
⇒ AB2 = AH.AO (Hệ thức lượng trong tam giác vuông)
⇒ AH.AO = AD.AE
⇒
Mà
⇒ ∆ADH ∽ ∆AOE (c.g.c)
⇒
⇒ DHOE nội tiếp
⇒
⇒
Nên: HB là phân giác
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho ∆ABC vuông tại A, đường cao AH. Biết 3AB = 2AC. Tính
Xem lời giải »
Câu 2:
Cho tam giác ABC ( AB > BC) có AB + BC = 11cm, . Bán kính đường tròn nội tiếp tam giác ABC là cm. Tính đường cao AH của tam giác ABC.
Xem lời giải »
Câu 3:
Cho C = 5 + 52 + … + 520. Chứng minh rằng C chia hết cho 5, 6, 13.
Xem lời giải »
Câu 6:
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Điểm M nằm giữa B và C, gọi I là trung điểm của AC, lấy điểm N đối xứng M qua I.
a) Tính độ dài cạnh BC?
b) Tứ giác AMCN là hình gì? Vì sao?
Xem lời giải »
Câu 7:
Cho tứ diện ABCD có M nằm trên cạnh AB, N nằm trên cạnh AD thoả MB = 2MA, AN = 2ND. Gọi P là điểm thuộc miền trong của tam giác BCD. Tìm giao tuyến của (MNP) và (ABC).
Xem lời giải »


