Cho đường tròn (O; R) có hai đường kính AB và CD vuông góc. Gọi I là điểm trên cung AC sao cho khi vẽ tiếp tuyến qua I và cắt DC kéo dài tại M thì IC = CM.
Câu hỏi:
Cho đường tròn (O; R) có hai đường kính AB và CD vuông góc. Gọi I là điểm trên cung AC sao cho khi vẽ tiếp tuyến qua I và cắt DC kéo dài tại M thì IC = CM. Độ dài OM tính theo bán kính là?
Trả lời:
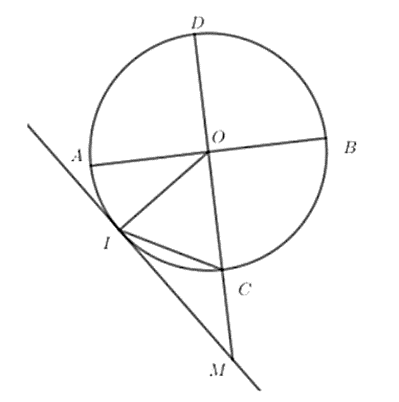
Ta có: (góc tạo bởi tiếp tuyến và dây cung với góc ở tâm chắn cung IC)
⇒
Lại có (do Δ∆CMI cân tại C)
Do đó Δ∆OIC đều (vì )
⇒
+) Xét Δ∆OIM vuông tại I có:
cos
⇒ OM = 2R.