Cho đường tròn (O; R) và hai bán kính OA, OB. Trên các bán kính
Câu hỏi:
Cho đường tròn (O; R) và hai bán kính OA, OB. Trên các bán kính OA, OB lần lượt là các điểm M, N sao cho OM = ON. Vẽ dây CD qua M và N (M nằm giữa C và N).
1. Chứng minh rằng CM = DN.
2. Giả sử \(\widehat {AOB} = 90^\circ \), hãy tính OM, ON theo R sao cho CM = MN = ND.
Trả lời:
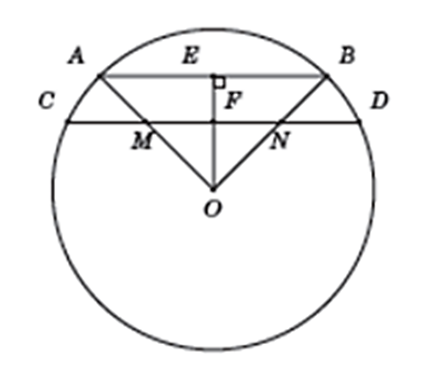
a) Hạ OE vuông góc với AB cắt CD tại F
Trong tam giác OAB cân tại O ta có:
\(\frac{{OM}}{{OA}} = \frac{{ON}}{{OB}} \Rightarrow MN\parallel AB \Rightarrow OF \bot MN\)
Và MF = NF
Ta nhận xét thêm:
OF ⊥ MN ⇔ OF ⊥ CD ⇔ CF ⊥ DF
Khi đó: CM = CF – MF = DF – NF = DN (đpcm)
b) Đặt MF = x, suy ra:
CF = CM + MF = MN + MF = 3MF = 3x
OF = x, vì tam giác OMF vuông cân tại F
Trong tam giác OCF, ta có:
OF2 = OC2 – CF2
⇔ x2 = R2 – 9x2
⇔ 10x2 = R2
⇔ x = \(\frac{R}{{\sqrt {10} }}\)
Khi đó ta được:
ON = OM = OF\(\sqrt 2 = \frac{R}{{\sqrt {10} }}.\sqrt 2 = \frac{R}{{\sqrt 5 }}\)
Vậy với OM = ON = \(\frac{R}{{\sqrt 5 }}\) thỏa mãn điều kiện bài toán.

