Cho hình chữ nhật ABCD. Qua C kẻ đường thẳng vuông góc với AC cắt đường thẳng AB, AD theo thứ tự tại E, F.
Câu hỏi:
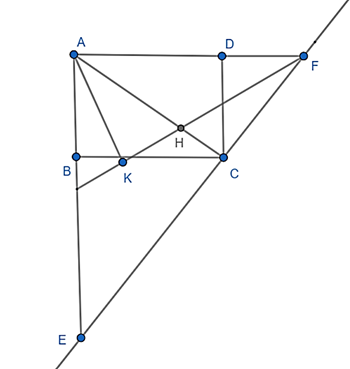
Cho hình chữ nhật ABCD. Qua C kẻ đường thẳng vuông góc với AC cắt đường thẳng AB, AD theo thứ tự tại E, F. Tia phân giác của góc AFE cắt AC tại H. Gọi K là hình chiếu của A trên FH.
a) Biết AB = 4cm, AC = 6cm. Tính AE, DE.
b) Chứng minh AB.AE = AD.AF.
Trả lời:
a) CB2 = AB2 + AC2 = 42 + 62 = 52
Suy ra: (cm)
Xét tam giác vuông ACE (vì CE vuông góc AC) có CB vuông góc AE
Nên: CA2 = AB.AE
⇒ (cm)
DE2 = AE2 + AD2 = 92 + BC2 = 92 + 52 = 1333
⇒ cm
b) Xét tam giác BAC và tam giác AEC có:
Chung
⇒ ∆ABC ∽ ∆ACE (g.g)
⇒ ⇒ AC2 = AB.AE (1)
Xét tam giác vuông ACF tại C có DC là đường cao, có:
AD.AF = AC2 (2)
Từ (1) và (2): AB.AE = AD.AF
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho ∆ABC vuông tại A, đường cao AH. Biết 3AB = 2AC. Tính
Xem lời giải »
Câu 2:
Cho tam giác ABC ( AB > BC) có AB + BC = 11cm, . Bán kính đường tròn nội tiếp tam giác ABC là cm. Tính đường cao AH của tam giác ABC.
Xem lời giải »
Câu 3:
Cho C = 5 + 52 + … + 520. Chứng minh rằng C chia hết cho 5, 6, 13.
Xem lời giải »
Câu 5:
Tìm nghiệm âm lớn nhất của phương trình tan5x.tanx = 1.
Xem lời giải »
Câu 6:
Cho hàm số y = ax + 3. Hãy xác định hệ số a trong trường hợp sau:
Đồ thị của hàm số song song với đường thẳng y = -2x.
Xem lời giải »
Câu 7:
Cho (O; R) đường kính AB và M nằm trên (O; R) với MA < MB (M khác A và B). Tiếp tuyến tại M của (O; R) cắt tiếp tuyến tại A và B của (O; R) theo thứ tự ở C và D.
a) Chứng minh ACDB là hình thang vuông
b) AD cắt (O; R) tại E, OD cắt MB tại N. Chứng minh OD vuông góc MB và DE.DA = DN.DO
c) Cho AM = R. Tính theo R diện tích ACDB.
Xem lời giải »
Câu 8:
Cho y = ax – 3.
a) Đồ thị cắt đường thẳng y = 2x - 1 tại điểm có hoành độ là 2.
b) Đồ thị hàm số cắt đường thẳng y = -3x + 2 tại điểm có tung độ là 3.
Xem lời giải »


