Cho tam giác ABC vuông tại A, đường cao AH, M là điểm bất kì
Câu hỏi:
Cho tam giác ABC vuông tại A, đường cao AH, M là điểm bất kì thuộc cạnh BC. Kẻ MI vuông góc với AC (I thuộc AC), kẻ MK vuông góc với AB (K ∈ AD).
a) Chứng minh KI = MA.
b) Gọi O là giao điểm của AM và KI. Chứng minh \(\widehat {IHK} = 90^\circ \).
Trả lời:
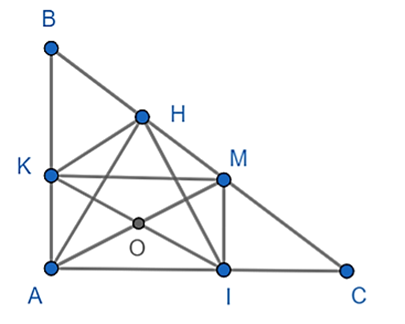
a) Xét tứ giác AIMK có: \(\widehat A = \widehat K = \widehat I = 90^\circ \)
Nên AIMK là hình chữ nhật
⇒ AM cắt KI tại trung điểm mỗi đường (tại O) và AM = KI
b) AIMK là hình chữ nhật, O là giao KI và AM
⇒ O là tâm đường tròn ngoại tiếp tứ giác AMKI
Hay A, K, M, I cùng thuộc đường tròn tâm O có bán kính là R = OK = OI = OA = OM
Lại có: \(\widehat {AHM} = 90^\circ \) mà O là trung điểm AM
Nên OH = OA = OM = \(\frac{1}{2}AM\)
Suy ra: OH = OA = OM = OK = OI
Xét tam giác HIK có: OH = OK = OI =\(\frac{1}{2}KI\)
Suy ra: tam giác HIK vuông tại H hay \(\widehat {IHK} = 90^\circ \).

