Cho tam giác ABC vuông tại A và đường cao AH (H ∈ BC). 1) Cho AH = 6; BH = 3. Tính BC và số đo (góc làm tròn đến phút). 2) Đường thẳng vuông góc với BC tại B cắt tia CA tại K. Hạ AE ⊥ BK (E

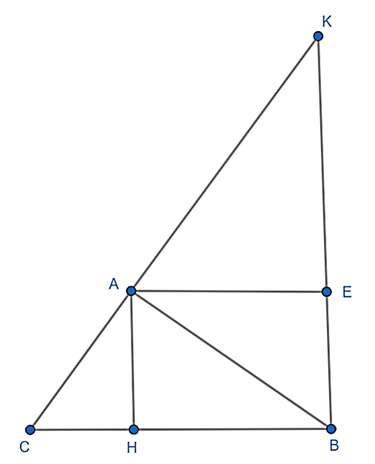
1) Áp dụng hệ thức lượng giác vào tam giác ABC vuông tại A có đường cao AH

AH² = BH.HC

⇒ 6²= 3. HC ⇒ HC = 6² : 3= 12cm

Ta có : BC = BH + HC = 3 + 12 =15 cm

$$\begin{gathered} \frac{1}{A{H}^2}=\frac{1}{A{B}^2}+\frac{1}{A{C}^2}\Rightarrow AC=6\sqrt{5} \\ AB=\sqrt{A{H}^2+B{H}^2}=\sqrt{3^2+6^2}=3\sqrt{5} \end{gathered}$$

Xét tam giác BAC vuông tại A có: sin$\widehat{ABC}=\frac{AC}{BC}=\frac{6\sqrt{5}}{15}=\frac{2\sqrt{5}}{5}\Rightarrow \widehat{ABC}=63°$

2) Xét tam giác BAK và tam giác CAB có:

$\widehat{BAK}=\widehat{BAC}=90°$

$\widehat{BKA}=\widehat{ABC}$ (cùng phụ với $\widehat{KBA}$)

Suy ra: ∆BAK ∽ ∆CAB (g.g)

⇒ $\frac{BA}{AC}=\frac{AK}{AB}\Rightarrow A{B}^2=AK.AC$

Lại có: ABHE là hình chữ nhật vì $\widehat{H}=\widehat{B}=\widehat{E}=90°$ nên AB = HE

Suy ra: EH² = AK.AC (1)

Xét tam giác BEA và tam giác AEK có:

$$\begin{gathered} \widehat{BEA}=\widehat{AEK}=90° \\ \widehat{ABE}=\widehat{KAE}=90°-\widehat{EAB} \end{gathered}$$

Suy ra: ∆BEA ∽ ∆AEK (g.g)

⇒ $\frac{BE}{AE}=\frac{AE}{EK}$⇒ BE.EK = AE²

Xét tam giác BHA và tam giác AHC có:

$$\begin{gathered} \widehat{BHA}=\widehat{CHA}=90° \\ \widehat{ABH}=\widehat{CAH}=90°-\widehat{ACH} \end{gathered}$$

Suy ra: ∆BHA ∽ ∆AHC (g.g)

⇒ $\frac{BH}{AH}=\frac{AH}{HC}$ ⇒ AH² = BH.HC

⇒ BH.HC + BE.EK = AE² + AH² = EH² (2)

Từ (1) và (2) suy ra: BH.HC + BE.EK = AK.AC.