Cho tam giác nhọn ABC. Chứng minh S ABC = 1/2 BC. BA.. sin B = 1/2 AB. AC . sin A = 1/2 CA. CB. sin C
Câu hỏi:
Cho tam giác nhọn ABC. Chứng minh .
Trả lời:
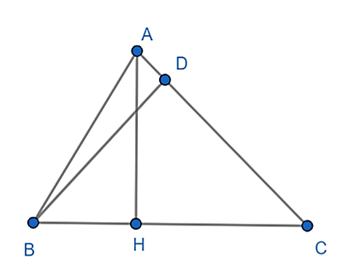
Kẻ đường cao AH, BD
(*)
Mà tam giác AHB vuông tại H nên:
Khi đó:
Tương tự: Trong tam giác AHC vuông tại H có:
Khi đó:
Ta có: (*)
Trong tam giác BAD vuông tại D có:
Thay vào (*) có: .