Câu hỏi:
Cho tứ diện ABCD có các cạnh AB,AC và AD đôi một vuông góc với nhau; AB=6a, AC=7a và AD=4a. Gọi M, N, P tương ứng là trung điểm các cạnh BC, CD, BD. Tính thể tích V của tứ diện AMNP
A. V=72a3.
Trả lời:
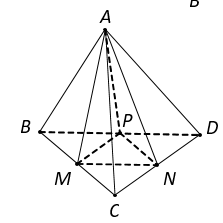
Do AB, AC và AD đôi một vuông góc với nhau nên
VABCD=16AB.AC.AD=16.6a.7a.4a=28a3.
Dễ thấy SΔMNP=14SΔBCD .
Suy ra VAMNP=14VABCD=7a3 . Chọn D.
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SA=a√2. Tính thể tích V của khối chóp S.ABCD
Câu 2:
Cho hình chóp S.ABC có tam giác SBC là tam giác vuông cân tại S, SB=2a và khoảng cách từ A đến mặt phẳng (SBC) bằng 3a. Tính theo a thể tích V của khối chóp S.ABC
Câu 3:
Cho khối chóp S.ABC có SA vuông góc với đáy, SA=4, AB=6, BC=10 và CA=8 . Tính thể tích V của khối chóp S.ABC.
Câu 4:
Câu 5:
Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BCD. Tính thể tích V của khối chóp A.GBC.
Câu 6:
Câu 7:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân ở B, AC=a√2 , SA=a và vuông góc với đáy (ABC) . Gọi G là trọng tâm tam giác SBC. Mặt phẳng (α) qua AG và song song với BC cắt SB, SC lần lượt tại M, N. Tính theo a thể tích V của khối chóp S.AMN.
Câu 8:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M và N lần lượt là trung điểm của các cạnh AB và AD; H là giao điểm của CN và DM. Biết SH vuông góc với mặt phẳng (ABCD) và SH=a√3 . Tính thể tích khối chóp S.CDNM.
