Cho tứ diện ABCD có diện tích tam giác ABC= 4 cm^2, ABD= 6 cm^2, AB= 3cm

Câu hỏi:

Cho tứ diện ABCD có $S_{Δ A B C} = 4 {cm}^{2}, S_{Δ A B D} = 6 {cm}^{2}, A B = 3 cm$ . Góc giữa hai mặt phẳng $(A B C)$ và $(A B D)$ bằng $60^{ο}$ . Tính thể tích V của khối tứ diện đã cho.

A. $V = \frac{2 \sqrt{3}}{3} {cm}^{3}$ .

B. $V = \frac{4 \sqrt{3}}{3} {cm}^{3}$ .

C. $V = 2 \sqrt{3} {cm}^{3}$ .

D. $V = \frac{8 \sqrt{3}}{3} {cm}^{3}$ .

Trả lời:

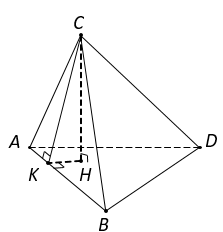
Media VietJack

Kẻ $C K ⊥ A B$ . Ta có $S_{Δ A B C} = \frac{1}{2} A B . C K \overset{}{\to} C K = \frac{8}{3} cm.$

Gọi H là chân đường cao của hình chóp hạ từ đỉnh C.

Xét tam giác vuông CHK, ta có $C H = C K . \sin \hat{C K H} = C K . \sin \hat{(A B C), (A B D)} = \frac{4 \sqrt{3}}{3} .$

Vậy thể tích khối tứ diện $V = \frac{1}{3} S_{Δ A B D} . C H = \frac{8 \sqrt{3}}{3} {cm}^{3} .$ Chọn D.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và $S A = a \sqrt{2} .$ Tính thể tích V của khối chóp S.ABCD

Xem lời giải »

Câu 2:

Cho hình chóp S.ABC có tam giác SBC là tam giác vuông cân tại S, $S B = 2 a$ và khoảng cách từ A đến mặt phẳng $(S B C)$ bằng $3 a .$ Tính theo a thể tích V của khối chóp S.ABC

Xem lời giải »

Câu 3:

Cho khối chóp S.ABC có SA vuông góc với đáy, $S A = 4, A B = 6, B C = 10$ và $C A = 8$ . Tính thể tích V của khối chóp S.ABC.

Xem lời giải »

Câu 4:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh

A B = a

B C = 2 a

. Hai mặt bên

(S A B)

và

(S A D)

cùng vuông góc với mặt phẳng đáy

(A B C D)

, cạnh SA. Tính theo a thể tích V của khối chóp S.ABCD

Xem lời giải »

Câu 5:

Cho tứ diện ABCD có các cạnh AB,AC và AD đôi một vuông góc với nhau; $A B = 6 a, A C = 7 a$ và $A D = 4 a .$ Gọi $M, N, P$ tương ứng là trung điểm các cạnh $B C, C D, B D .$ Tính thể tích V của tứ diện AMNP

Xem lời giải »

Câu 6:

Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BCD. Tính thể tích V của khối chóp A.GBC.

Xem lời giải »

Câu 7:

Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và khoảng cách từ A đến mặt phẳng

(S B C)

bằng

\frac{a \sqrt{2}}{2}

. Tính thể tích V của khối chóp đã cho.

Xem lời giải »

Câu 8:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân ở B, $A C = a \sqrt{2}$ , SA=a và vuông góc với đáy $(A B C)$ . Gọi G là trọng tâm tam giác SBC. Mặt phẳng $(α)$ qua AG và song song với BC cắt SB, SC lần lượt tại M, N. Tính theo a thể tích V của khối chóp S.AMN.

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Cho tứ diện ABCD có diện tích tam giác ABC= 4 cm^2, ABD= 6 cm^2, AB= 3cm

Xem thêm bài tập Toán có lời giải hay khác: