Xét các số thực dương a,b,x,y thỏa mãn a>1,b>1 và a^x=b^y=căn ab. Giá trị nhỏ nhất của biểu thức P=x+2y thuộc tập hợp nào dưới đây?

Câu hỏi:

Xét các số thực dương $a, b, x, y$ thỏa mãn $a > 1, b > 1$ và $a^{x} = b^{y} = \sqrt{a b}$ . Giá trị nhỏ nhất của biểu thức $P = x + 2 y$ thuộc tập hợp nào dưới đây?

A. $(1; 2)$

B. $[2; \frac{5}{2})$

C. $[3; 4)$

D. $[\frac{5}{2}; 3)$

Trả lời:

Chọn D

Ta có $a, b > 1$ và $x, y > 0$ nên $a^{x}; b^{y}; \sqrt{a b} > 1$

Do đó: $a^{x} = b^{y} = \sqrt{a b}$ $\Leftrightarrow \log_{a} a^{x} = \log_{a} b^{y} = \log_{a} \sqrt{a b} \Leftrightarrow \{\begin{cases} x = \frac{1}{2} + \frac{1}{2} \log_{a} b \\ 2 y = 1 + \log_{b} a \end{cases}$ .

Khi đó, ta có: $P = \frac{3}{2} + \frac{1}{2} \log_{a} b + \log_{b} a$ .

Lại do $a, b > 1$ nên $\log_{a} b, \log_{b} a > 0$ .

Suy ra $P \geq \frac{3}{2} + 2 \sqrt{\frac{1}{2} \log_{a} b . \log_{b} a} = \frac{3}{2} + \sqrt{2}$ , $P = \frac{3}{2} + \sqrt{2} \Leftrightarrow \log_{a} b = \sqrt{2}$ .

Lưu ý rằng, luôn tồn tại $a, b > 1$ thỏa mãn $\log_{a} b = \sqrt{2}$ .

Vậy $\min P = \frac{3}{2} + \sqrt{2} \in [\frac{5}{2}; 3)$ .

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Với a là số thực dương tùy ý,

\log_{2} 2 a

bằng

Xem lời giải »

Câu 2:

Nghiệm của phương trình $\log_{2} (x + 6) = 5$ là

Xem lời giải »

Câu 3:

Với

a, b

là các số thực dương tùy ý thỏa mãn

\log_{3} a - 2 \log_{9} b = 3

, mệnh đề nào dưới đây đúng?

Xem lời giải »

Câu 4:

Tập nghiệm của bất phương trình $\log_{3} (36 - x^{2}) \geq 3$ là

Xem lời giải »

Câu 5:

Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn $\log_{3} (x + y) = \log_{4} (x^{2} + y^{2})$ ?

Xem lời giải »

Câu 6:

Cho phương trình $\log_{2}^{2} (2 x) - (m + 2) \log_{2} x + m - 2 = 0$ (m là tham số thực). Tập hợp tất cả các giá trị của m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn $[1; 2]$ .

Xem lời giải »

Câu 7:

Có bao nhiêu cặp số nguyên $(x; y)$ thỏa mãn $0 \leq x \leq 2000$ và $\log_{3} (3 x + 3) + x = 2 y + 9^{y}$ ?

Xem lời giải »

Câu 8:

Cho phương trình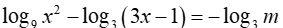 Cho phương trình log9x^2-log3(3x-1)=-log3m ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên của m để phương trình (ảnh 1) (m là tham số thực). Có tất cả bao nhiêu giá trị nguyên của m để phương trình đã cho có nghiệm

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Xét các số thực dương a,b,x,y thỏa mãn a>1,b>1 và a^x=b^y=căn ab. Giá trị nhỏ nhất của biểu thức P=x+2y thuộc tập hợp nào dưới đây?

Xem thêm bài tập Toán có lời giải hay khác: