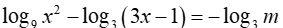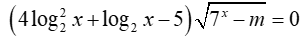Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn log3(x+y)=log(x^2+y^2) ?
Câu hỏi:
Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn log3(x+y)=log4(x2+y2) ?
A. 3
B. 2
C. 1
D. Vô số
Trả lời:
Chọn B.
Điều kiện: {x+y>0x2+y2>0.
Điều kiện cần
Đặt t=log3(x+y)=log4(x2+y2)⇒{x+y=3t(d)x2+y2=4t(C) .
Suy ra x, y tồn tại nếu đường thẳng d cắt đường tròn (C) tại ít nhất một điểm.
Hay |−3t|√2≤2t⇒t≤log32√2≈0,8548.
Khi đó:
x2+y2≤4log32√2≈3,27⇒{0≤x2≤3x∈ℤ⇒[x=−1x=0x=1.
Điều kiện đủ:
Với x=−1⇒{y=3t+1y2=4t−1⇒{4t−1>04t−1=(3t+1)2⇒{t>0f(t)=9t+2.3t+2−4t=0 .
Khi 0<t<0,8548⇒9t≥4t⇒f(t)>0 . Suy x=−1(l) .
Với x=0⇒{y=3ty2=4t⇒4t=3t⇒t=0⇒y=1(t/m) .
x=1⇒{y=3t−1y2=4t−1⇒y=t=0(t/m) .
Xem thêm bài tập Toán có lời giải hay khác:
Câu 3:
Với a,b là các số thực dương tùy ý thỏa mãn log3a−2log9b=3 , mệnh đề nào dưới đây đúng?
Xem lời giải »
Câu 4:
Tập nghiệm của bất phương trình log3(36−x2)≥3 là
Xem lời giải »
Câu 5:
Cho phương trình log22(2x)−(m+2)log2x+m−2=0 (m là tham số thực). Tập hợp tất cả các giá trị của m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn [1; 2] .
Xem lời giải »
Câu 6:
Có bao nhiêu cặp số nguyên (x; y) thỏa mãn 0≤x≤2000 và log3(3x+3)+x=2y+9y?
Xem lời giải »
Câu 7:
Cho phương trình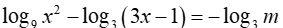
(m là tham số thực). Có tất cả bao nhiêu giá trị nguyên của m để phương trình đã cho có nghiệm
Xem lời giải »
Câu 8:
Cho phương trình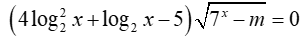
( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt
Xem lời giải »
