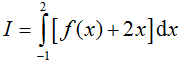Một nguyên hàm F(x) của hàm số f(x)=x/cos^2 x thỏa mãn F(π)=2017. Khi đó F(x) là hàm số

Câu 1:

Tìm nguyên hàm: $I=\int \frac{{\sin }^{4}x}{{\cos }^{2}x}dx$

Xem lời giải »

Câu 2:

Tìm nguyên hàm: $I=\int {\cos }^{4}2xdx$

Xem lời giải »

Câu 3:

Tìm nguyên hàm: $J=\int \left(\cos 3x.\cos 4x+{\sin }^{3}2x\right)dx$

Xem lời giải »

Câu 4:

Tìm nguyên hàm: $I=\int \left(\frac{1}{{\ln }^{2}x}-\frac{1}{\ln x}\right)dx$

Xem lời giải »

Câu 5:

Tính $F\left(x\right)=\int \frac{1+x\sin x}{{\cos }^{2}x}dx$ . Chọn kết quả đúng

Xem lời giải »

Câu 6:

Một nguyên hàm F(x) của hàm số $f\left(x\right)=\sin x+\frac{1}{{\cos }^{2}x}$ thỏa mãn điều kiện $F\left(\frac{\mathrm{\pi }}{4}\right)=\frac{\sqrt{2}}{2}$  là

Xem lời giải »

Câu 7:

Một nguyên hàm F(x) của hàm số $f\left(x\right)=2\sin 5x+\sqrt{x}+\frac{3}{5}$ thỏa mãn đồ thị của hai hàm số F(x) và f(x) cắt nhau tại một điểm nằm trên trục tung là:

Xem lời giải »

Câu 8:

Cho hàm số f(x) liên tục trên khoảng (-2; 3). Gọi F(x) là một nguyên hàm của f(x) trên khoảng (-2; 3). Tính 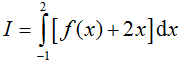, biết F(-1) = 1, F(2) = 4.

Xem lời giải »