Trong không gian Oxyz, cho điểm A (1; -1; 1) và hai đường thẳng delta x-1 / 2 = y / 1 =z - 3/ -1
Câu hỏi:
Trong không gian Oxyz, cho điểm A (1; -1; 1) và hai đường thẳng .
Phương trình đường thẳng đi qua điểm A và cắt cả hai đường thẳng Δ, Δ' là:
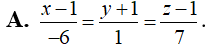
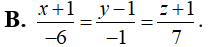
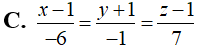
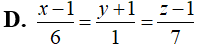
Trả lời:
Chọn C
Gọi d là đường thẳng cần tìm.
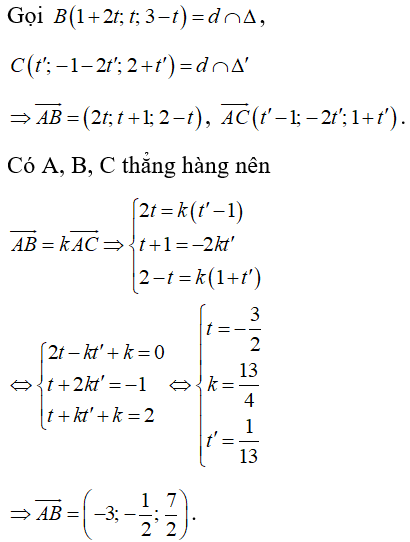
Đường thẳng cần tìm qua A và nhận 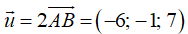 là véc tơ chỉ phương nên có phương trình:
là véc tơ chỉ phương nên có phương trình:
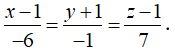
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt cầu (S) có tâm nằm trên đường thẳng và tiếp xúc với hai mặt phẳng (P): 2x - z - 4 = 0, (Q): x – 2y – 2 = 0
Xem lời giải »
Câu 2:
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (S): x + 2y – 2z + 2018 = 0 và (Q): x + my + (m -1)z + 2017 = 0. Khi hai mặt phẳng (P) và (Q) tạo với nhau một góc nhỏ nhất thì điểm H nào dưới đây nằm trong mặt phẳng (Q)?
Xem lời giải »
Câu 3:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng chéo nhau
Phương trình mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng trên là:
Xem lời giải »
Câu 4:
Trong không gian với tọa độ Oxyz, cho hai điểm A (1;1;2), B (-1; 3; -9). Tìm tọa độ điểm M thuộc Oy sao cho vuông tại M.
Xem lời giải »
Câu 5:
Trong không gian Oxyz, cho hai đường thẳng và . Phương trình mặt phẳng chứa đường thẳng d và tạo với đường thẳng d' một góc lớn nhất là:
Xem lời giải »
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng (α): x - y + z - 4 = 0 và mặt cầu (S): (x-3)²+ (y-1)²+ (z-2)² =16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
Xem lời giải »
Câu 7:
Trong không gian Oxyz, cho tam giác ABC có A (2;3;3), phương trình đường trung tuyến kẻ từ B là , phương trình đường phân giác trong của góc C là . Đường thẳng BC có một vectơ chỉ phương là:
Xem lời giải »
Câu 8:
Cho hình chóp S. ABCD có đáy ABCD là hình vuông, tam giác SAB cân tại S. Góc giữa mặt bên (SAB) và mặt đáy bằng , góc giữa SA và mặt phẳng đáy bằng 450. Biết thể tích khối chóp S. ABCD bằng . Chiều cao của hình chóp S. ABCD bằng:
Xem lời giải »
là véc tơ chỉ phương nên có phương trình:

