Cho hình chóp SABCD có đáy là hình bình hành ABCD. Gọi M, N lần lượt là trung điểm AB, SC. a) Xác định giao điểm I, K của AN, MN với (SBD).
Câu hỏi:
Cho hình chóp SABCD có đáy là hình bình hành ABCD. Gọi M, N lần lượt là trung điểm AB, SC.
a) Xác định giao điểm I, K của AN, MN với (SBD).
b) Tính tỉ số .
c) Chứng minh B, I, K thẳng hàng. Tính tỉ sốTrả lời:
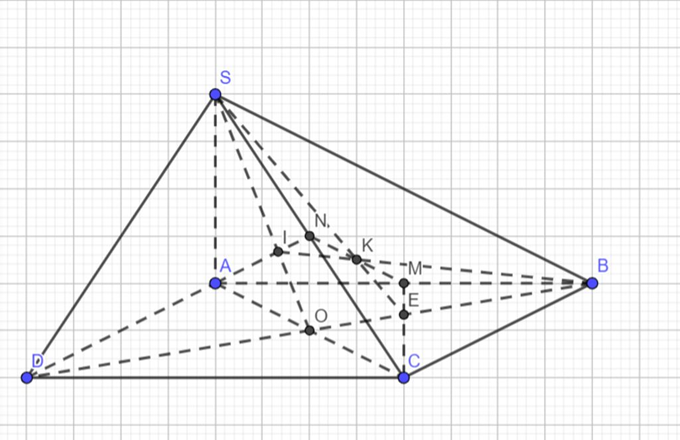
a) Gọi AC ∩ BD = O, SO ∩ AN = I
⇒ AN ∩ (SBD) = I
CM ∩ BO = E, SE ∩ MN = K ⇒ MN ∩ (SBD) = K
b, c) Ta có M, N là trung điểm AB, SC; O là trung điểm AC, BD
⇒ I, E là trọng tâm SAC, BAC
⇒
Ta có: M, K, N thẳng hàng; M ∈ CE, K ∈ SE, N ∈ SC
Suy ra:
⇒
⇒
⇒
Vậy B, I, K thẳng hàng (định lý Menelauyt)
Ta có: S, K, E thẳng hàng nên
⇒
⇒
Lại có từ S, K, E thẳng hàng nên
⇒
⇒
⇒
Hay
Suy ra: .
