Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông

Câu hỏi:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa mặt phẳng $(S B D)$ và mặt phẳng $(A B C D)$ bằng $60^{0}$ . Tính theo a thể tích V của khối chóp S.ABCD.

A. $V = \frac{a^{3} \sqrt{6}}{12}$ .

$V = a^{3}$

$V = \frac{a^{3} \sqrt{6}}{6}$ .

D. $V = \frac{a^{3} \sqrt{6}}{2}$ .

Trả lời:

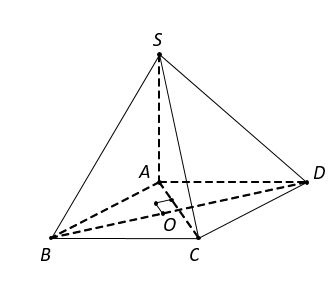
Media VietJack

Vì $S A ⊥ (A B C D) \Rightarrow S A ⊥ B D (1)$ .

Gọi $O = A C \cap B D$ , suy ra $B D ⊥ A O (2)$ .

Từ

$(1)$ và

$(2)$ , suy ra

$B D ⊥ (S A O) \Rightarrow B D ⊥ S O$

Do $\{\begin{cases} (S B D) \cap (A B C D) = B D \\ S O ⊥ B D, A O ⊥ B D \end{cases}$ , suy ra

$60^{0} = [\hat{(S B D), (A B C D)}] = [\hat{S O, A O}] = \hat{S O A}$

Tam giác vuông SAO, ta có $S A = A O . \tan \hat{S O A} = \frac{a \sqrt{6}}{2}$ .

Diện tích hình vuông ABCD là $S_{A B C D} = a^{2}$ .

Vậy $V_{S . A B C D} = \frac{1}{3} S_{A B C D} . S A = \frac{a^{3} \sqrt{6}}{6} .$ Chọn C.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và $S A = a \sqrt{2} .$ Tính thể tích V của khối chóp S.ABCD

Xem lời giải »

Câu 2:

Cho hình chóp S.ABC có tam giác SBC là tam giác vuông cân tại S, $S B = 2 a$ và khoảng cách từ A đến mặt phẳng $(S B C)$ bằng $3 a .$ Tính theo a thể tích V của khối chóp S.ABC

Xem lời giải »

Câu 3:

Cho khối chóp S.ABC có SA vuông góc với đáy, $S A = 4, A B = 6, B C = 10$ và $C A = 8$ . Tính thể tích V của khối chóp S.ABC.

Xem lời giải »

Câu 4:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh

$A B = a$ ,

$B C = 2 a$ . Hai mặt bên

$(S A B)$ và

$(S A D)$ cùng vuông góc với mặt phẳng đáy

$(A B C D)$ , cạnh SA. Tính theo a thể tích V của khối chóp S.ABCD

Xem lời giải »

Câu 5:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, đường chéo AC=a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc giữa $(S C D)$ và đáy bằng $45^{0}$ . Tính theo a thể tích V của khối chóp S.ABCD.

Xem lời giải »

Câu 6:

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, $A D = D C = 1, A B = 2$ ; cạnh bên SA vuông góc với đáy; mặt phẳng $(S B C)$ tạo với mặt đáy $(A B C D)$ một góc $45^{0}$ . Tính thể tích V của khối chóp S.ABCD.

Xem lời giải »

Câu 7:

Cho tứ diện ABCD có $S_{Δ A B C} = 4 {cm}^{2}, S_{Δ A B D} = 6 {cm}^{2}, A B = 3 cm$ . Góc giữa hai mặt phẳng $(A B C)$ và $(A B D)$ bằng $60^{ο}$ . Tính thể tích V của khối tứ diện đã cho.

Xem lời giải »

Câu 8:

Cho tứ diện ABCD có các cạnh AB,AC và AD đôi một vuông góc với nhau; $A B = 6 a, A C = 7 a$ và $A D = 4 a .$ Gọi $M, N, P$ tương ứng là trung điểm các cạnh $B C, C D, B D .$ Tính thể tích V của tứ diện AMNP

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông

Xem thêm bài tập Toán có lời giải hay khác: