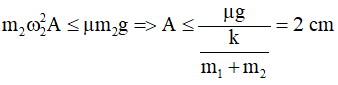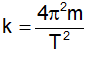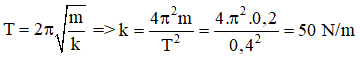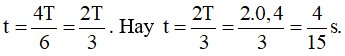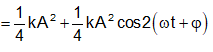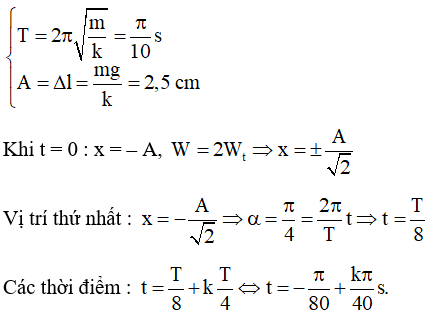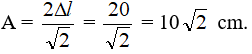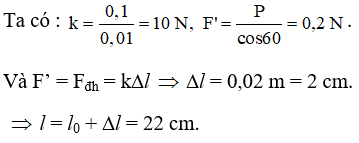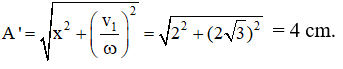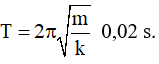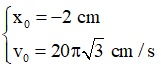Bài tập trắc nghiệm Con lắc lò xo có lời giải - Vật Lí lớp 12

---

Bài tập trắc nghiệm Con lắc lò xo có lời giải

Với Bài tập trắc nghiệm Con lắc lò xo có lời giải Vật Lí lớp 12 tổng hợp 60 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Con lắc lò xo từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

Câu 1: Phát biểu nào sau đây là không đúng với con lắc lò xo ngang?

A. Chuyển động của vật là chuyển động thẳng.

B. Chuyển động của vật là chuyển động biến đổi đều.

C. Chuyển động của vật là chuyển động tuần hoàn.

D. Chuyển động của vật là một dao động điều hoà.

Lời giải:

Chọn B. Với con lắc lò xo ngang vật chuyển động thẳng, dao động điều hoà.

Câu 2: Con lắc lò xo ngang dao động điều hoà, vận tốc của vật bằng không khi vật chuyển động qua

A. vị trí cân bằng.

B. vị trí vật có li độ cực đại.

C. vị trí mà lò xo không bị biến dạng.

D. vị trí mà lực đàn hồi của lò xo bằng không.

Lời giải:

Chọn B. Khi vật ở vị trí có li độ cực đại thì vận tốc của vật bằng không. Ba phương án còn lại đều là VTCB, ở VTCB vận tốc của vật đạt cực đại.

Câu 3: Một vật nặng treo vào một lò xo làm lò xo giãn ra 0,8 cm. Lấy g = 10 m/s². Chu kỳ dao động của vật là:

A. T = 0,178 s.

B. T = 0,057 s.

C. T = 222 s.

D. T = 1,777 s

Lời giải:

Chọn A. Chu kỳ dao động của con lắc lò xo dọc được tính theo công thức:

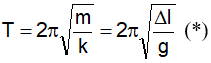
Đổi đơn vị 0,8 cm = 0,008 m rồi thay vào công thức (*) ta được T = 0,178s.

Câu 4: Trong dao động điều hoà của con lắc lò xo, phát biểu nào sau đây là không đúng?

A. Lực kéo về phụ thuộc vào độ cứng của lò xo.

B. Lực kéo về phụ thuộc vào khối lượng của vật nặng.

C. Gia tốc của vật phụ thuộc vào khối lượng của vật.

D. Tần số góc của vật phụ thuộc vào khối lượng của vật.

Lời giải:

Chọn B. Lực kéo về (lực phục hồi) có biểu thức F = - kx không phụ thuộc vào khối lượng của vật.

Câu 5: Con lắc lò xo gồm vật khối lượng m và lò xo có độ cứng k, dao động điều hoà với chu kỳ

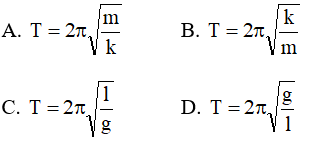
Lời giải:

Chọn A. Con lắc lò xo gồm vật khối lượng m và lò xo có độ cứng k, dao động điều hoà với chu kỳ

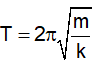
Câu 6: Con lắc lò xo dao động điều hoà, khi tăng khối lượng của vật lên 4 lần thì tần số dao động của vật

A. tăng lên 4 lần.

B. giảm đi 4 lần.

C. tăng lên 2 lần.

D. giảm đi 2 lần.

Lời giải:

Chọn D. Tần số dao động của con lắc là 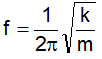khi tăng khối lượng của vật lên 4 lần thì tần số của con lắc giảm 2 lần.

Câu 7: Con lắc lò xo gồm vật m = 100g và lò xo k = 100 N/m. Lấy π² = 10. Dao động điều hoà với chu kỳ là:

A. T = 0,1 s.

B. T = 0,2 s.

C. T = 0,3s.

D. T = 0,4s.

Lời giải:

Chọn B. Con lắc lò xo gồm vật khối lượng m và lò xo có độ cứng k, dao động điều hoà với chu kỳ 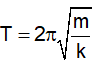, thay m = 100g = 0,1kg; k = 100 N/m và π² = 10 ta được T = 0,2 s.

Câu 8: Con lắc lò xo gồm vật m = 200g và lò xo k = 50N/m. Lấy π² = 10. Dao động điều hoà với chu kỳ là

A. T = 0,2s.

B. T = 0,4s.

C. T = 50s.

D. T = 100s.

Lời giải:

Chọn B. Tương tự câu 5.

Câu 9: Một con lắc lò xo dao động điều hoà với chu kỳ T = 0,5 s, khối lượng của quả nặng là m = 400g. Lấy π² = 10. Độ cứng của lò xo là

A. k = 0,156 N/m

B. k = 32 N/m

C. k = 64 N/m

D. k = 6400 N/m

Lời giải:

Chọn C. Áp dụng công thức tính chu kỳ 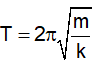ta suy ra k = 64 N/m

Câu 10: Con lắc lò xo ngang dao động với biên độ A = 8 cm, chu kỳ T = 0,5s, khối lượng của vật là m = 0,4 kg. Lấy π² = 10. Giá trị cực đại của lực đàn hồi tác dụng vào vật là

A. F_max = 525 N

B. F_max = 5,12 N

C. F_max = 256 N

D. F_max = 2,56 N

Lời giải:

Chọn B. Trong con lắc lò xo ngang lực đàn hồi tác dụng lên vật khi vật ở vị trí x là F = -kx, lực đàn hồi cực đại có độ lớn F_max = kA, với

Thay A = 8 cm = 0,8 m; T = 0,5s; m = 0,4 kg; π² = 10 ta được F_max = 5,12 N

Câu 11: Một con lắc lò xo gồm vật nặng khối lượng 0,4 kg gắn vào đầu lò xo có độ cứng 40 N/m. Người ta kéo quả nặng ra khỏi VTCB một đoạn 4 cm rồi thả nhẹ cho nó dao động. Phương trình dao động của vật nặng là

A. x = 4cos (10t)cm

B. x = 4cos (10t - π/2)cm.

C. x = 4cos (10πt - π/2)cm

D. x = 4cos (10πt + π/2)cm

Lời giải:

Chọn A. Vật dao động theo phương trình tổng quát x = Acos(ωt + φ). Tần số góc ω = √(k/m) = 10 rad/s. Từ cách kích thích ban đầu để tạo nên dao động ta có Acosφ = 4 cm và Asinφ = 0, từ đó tính được A = 4 cm, φ = 0. Thay vào phương trình tổng quát ta được x = 4cos(10t) cm

Câu 12: Một con lắc lò xo gồm vật nặng khối lượng 0,4 kg gắn vào đầu lò xo có độ cứng 40 N/m. Người ta kéo quả nặng ra khỏi VTCB một đoạn 4 cm rồi thả nhẹ cho nó dao động. Vận tốc cực đại của vật nặng là:

A. v_max = 160 cm/s.

B. v_max = 80 cm/s.

C. v_max = 40 cm/s.

D. v_max = 20 cm/s.

Lời giải:

Chọn C. Tốc độ góc

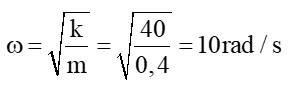
Vận tốc cực đại

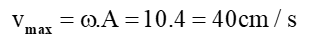
Câu 13: Một con lắc lò xo gồm vật nặng khối lượng 0,4 kg gắn vào đầu lò xo có độ cứng 40 N/m. Người ta kéo quả nặng ra khỏi VTCB một đoạn 4 cm rồi thả nhẹ cho nó dao động. Cơ năng dao động của con lắc là:

A. E = 320 J

B. E = 6,4.10^-2 J

C. E = 3,2.10^-2 J

D. E = 3,2 J

Lời giải:

Chọn C. Công thức tính cơ năng của con lắc lò xo

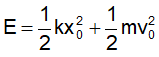
Đổi đơn vị và thay số ta được E = 3,2.10^-2 J

Câu 14: Con lắc lò xo gồm lò xo k và vật m, dao động điều hoà với chu kỳ T = 1 s. Muốn tần số dao động của con lắc là f’ = 0,5 Hz, thì khối lượng của vật m phải là

A. m’ = 2 m.

B. m’ = 3 m

C. m’ = 4 m

D. m’ = 5 m

Lời giải:

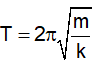
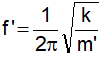
Chọn C. Con lắc gồm lò xo k và vật m dao động với chu kỳ con lắc gồm lò xo k và vật m’ dao động với tần số

Kết hợp với giả thiết T = 1s, f’ = 0,5 Hz suy ra m’ = 4 m

Câu 15: Một con lắc lò xo gồm một quả nặng có khối lượng m = 400 g và một lò xo có độ cứng k = 40 N/m. Người ta kéo quả nặng ra khỏi VTCB một đoạn bằng 8cm và thả cho nó dao động. Phương trình dao động của quả nặng là

A. x = 8cos0,1t (cm).

B. x = 8cos0,1πt (cm)

C. x = 8cos10πt (cm)

D. x = 8cos10t (cm)

Lời giải:

Chọn D. Xem hướng dẫn và làm tương tự câu 10

Câu 16: Một con lắc lò xo gồm quả nặng khối lượng 1kg và một lò xo có độ cứng 1600 N/m. Khi quả nặng ở VTCB, người ta truyền cho nó vận tốc ban đầu bằng 2 m/s. Biên độ dao động của quả nặng là

A. A = 5 m.        B. A = 5 cm.        C. A = 0,125 m.        D. A = 0,125 cm.

Lời giải:

Chọn B. Theo bảo toàn cơ năng trong dao động điều hoà ta có biểu thức tính biên độ dao động

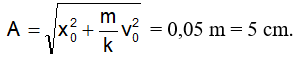
Câu 17: Một con lắc lò xo gồm quả nặng khối lượng 1kg và một lò xo có độ cứng 1600 N/m. Khi quả nặng ở VTCB, người ta truyền cho nó vận tốc ban đầu bằng 2 m/s theo chiều dương trục toạ độ. Phương trình li độ dao động của quả nặng là

A. x = 5cos(40t - π/2) m.

B. x = 0,5cos(40t + π/2) m

C. x = 5cos(40t - π/2) cm

D. x = 0,5cos(40t) cm

Lời giải:

Chọn C. Vật dao động theo phương trình tổng quát x = Acos(ωt + φ). Tần số góc ω = √(m/k) = 40 rad/s. Từ cách kích thích ban đầu để tạo nên dao động ta có Acosφ = 0 cm và - Asinφ = 200 cm/s, từ đó tính được A = 5 cm, φ = - π/2

Thay vào phương trình tổng quát ta được x = 5cos (40t - π/2)cm

Câu 18: Khi gắn quả nặng m₁ vào một lò xo, nó dao động với chu kỳ T₁ = 1,2s. Khi gắn quả nặng m₂ vào một lò xo, nó dao động với chu kỳ T₂ = 1,6s. Khi gắn đồng thời m₁ và m₂ vào lò xo đó thì chu kỳ dao động của chúng là

A. T = 1,4s        B. T = 2,0s        C. T = 2,8s        D. T = 4,0s

Lời giải:

Chọn B

Khi con lắc có khối lượng m₁ nó dao động với chu kỳ

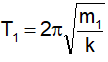
Khi con lắc có khối lượng m₂ nó dao động với chu kỳ

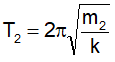
Khi gắn đồng thời m₁ và m₂ vào lò xo đó thì chu kỳ dao động của chúng là

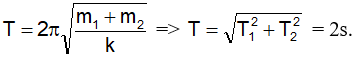
Câu 19: Khi mắc vật m vào lò xo k₁ thì vật m dao động với chu kỳ T₁ = 0,6s, khi mắc vật m vào lò xo k₂ thì vật m dao động với chu kỳ T₂ = 0,8s. Khi mắc vật m vào hệ hai lò xo k₁ nối tiếp với k₂ thì chu kỳ dao động của m là

A. T = 0,48s        B. T = 0,70s        C. T = 1,00s        D. T = 1,40s

Lời giải:

Chọn C

Khi độ cứng của lò xo là k₁ thì chu kỳ dao động của con lắc là

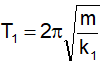
Khi độ cứng của lò xo là k₂ thì chu kỳ dao động của con lắc là

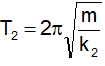
Khi hai lò xo k₁ và k₂ mắc nối tiếp thì chu kỳ dao động của con lắc là

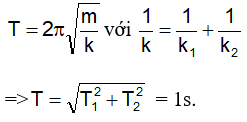
Câu 20: Khi mắc vật m vào lò xo k₁ thì vật m dao động với chu kỳ T₁ = 0,6s, khi mắc vật m vào lò xo k₂ thì vật m dao động với chu kỳ T₂ = 0,8s. Khi mắc vật m vào hệ hai lò xo k₁ song song với k₂ thì chu kỳ dao động của m là

A. T = 0,48s        B. T = 0,70s        C. T = 1,00s        D. T = 1,40s

Lời giải:

Chọn A

Khi độ cứng của lò xo là k₁ thì chu kỳ dao động của con lắc là

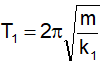
Khi độ cứng của lò xo là k₂ thì chu kỳ dao động của con lắc là

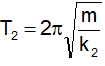
Khi hai lò xo k₁ và k₂ mắc song song thì chu kỳ dao động của con lắc là

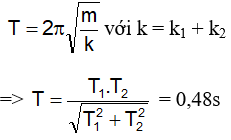
Câu 21: Con lắc lò xo gồm vật m và lò xo k dao động điều hòa, khi mắc thêm vào vật m một vật khác có khối lượng gấp 3 lần vật m thì chu kì dao động của chúng

A. tăng lên 3 lần

B. giảm đi 3 lần

C. tăng lên 2 lần

D. giảm đi 2 lần

Lời giải:

Chọn C. Chu kì dao động của hai con lắc :

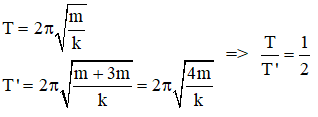
Câu 22: Khi treo vật m vào lò xo k thì lò xo giãn ra 2,5 cm, kích thích cho m dao động. Chu kì dao động tự do của vật là :

A. 1 s        B. 0,5 s        C. 0,32 s        D. 0,28 s

Lời giải:

Chọn C. Tại vị trí cân bằng trọng lực tác dụng vào vật cân bằng với lực đàn hồi của là xo:

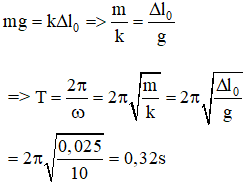
Câu 23: Một con lắc lò xo dao động thẳng đứng. Vật có khối lượng m = 0,2 kg. Trong 20 s con lắc thực hiện được 50 dao động. Tính độ cứng của lò xo

A. 60 N/m        B. 40 N/m        C. 50 N/m        D. 55 N/m

Lời giải:

Chọn C. Trong 20s con lắc thực hiện được 50 dao động, ta phải có : T = t/N = 0,4s.

Mặt khác:

Câu 24: Hai lò xo có chiều dài bằng nhau độ cứng tương ứng là k₁, k₂. Khi mắc vật m vào một lò xo k₁, thì vật m dao động với chu kì T₁ = 0,6 s. Khi mắc vật m vào lò xo k₂, thì vật m dao động với chu kì T₂ = 0,8 s. Khi mắc vật m vào hệ hai lò xo k₁ song song với k₂ thì chu kì dao động của m là.

A. 0,48 s        B. 0,7 s        C. 1,00 s        D. 1,4

Lời giải:

Chọn A. Chu kì T₁, T₂ xác định từ phương trình:

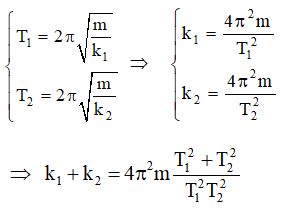
k₁, k₂ ghép song song, độ cứng của hệ ghép xác định từ công thức : k = k₁ + k₂. Chu kì dao động của con lắc lò xo ghép

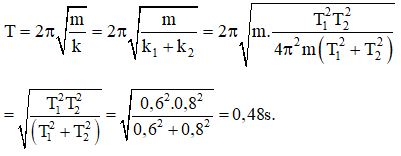
Câu 25: Vật có khối lượng m = 160 g được gắn vào lò xo có độ cứng k = 64 N/m đặt thẳng đứng, vật ở trên. Từ vị trí cân bằng, ấn vật xuống theo phương thẳng đứng đoạn 2,5 cm và buông nhẹ. Chọn trục Ox hướng lên, gốc tại vị trí cân bằng, gốc thời gian lúc buông vật. Lực tác dụng lớn nhất và nhỏ nhất lên giá đỡ là (g = 10 m/s²)

A. 3,2 N; 0 N        B. 1,6 N; 0 N         C. 3,2 N; 1,6 N         D. 1,760 N; 1,44 N

Lời giải:

Chọn A. Ta có:

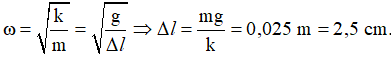
Từ vị trí cân bằng, ấn vật xuống theo phương thẳng đứng đoạn 2,5 cm và buông ⇒ Δl = A = 2,5 cm

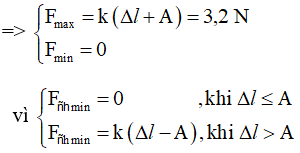
Câu 26: Trên mặt phẳng nghiêng α = 30° đặt con lắc lò xo. Vật có độ cứng 64 N/m, khối lượng vật là 160 g, vật ở dưới. Bỏ qua mọi ma sát. Từ vị trí cân bằng, kéo vật xuống theo phương trục lò xuống 1 đoạn 1 cm và buông nhẹ. Lực tác dụng lớn nhất và nhỏ nhất lên giá đỡ là (g = 10 m/s²)

A. 1,6N; 0N        B. 1,44N; 0,16N         C. 3,2N; 1,6N         D. 1,760N; 1,44N

Lời giải:

Chọn B

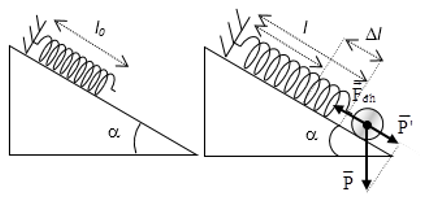
Ta có:

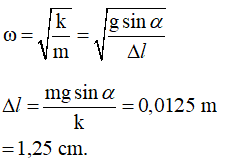
Từ vị trí cân bằng, ấn vật xuống theo phương thẳng đứng đoạn 1cm và buông ⇒ A = 1 cm.

⇒ F = k(Δl + A) = 1,44 N và F = k(Δl - A) = 0,16 N, khi Δl > A

Câu 27: Vật có khối lượng m = 160 g được gắn vào lò xo có độ cứng k = 64 N/m đặt thẳng đứng, vật ở dưới. Từ vị trí cân bằng, ấn vật xuống theo phương thẳng đứng đoạn 2,5 cm và buông nhẹ. Chọn trục Ox hướng lên, gốc tại vị trí cân bằng, gốc thời gian lúc buông vật. Phương trình dao động của vật là :

A. 2,5cos(20t + π) mm

B. 2,5cos(20t + π/2) cm

C. 2,5cos(20t + π) cm

D. 5cos(20t + π) cm

Lời giải:

Chọn C. Phương trình dao động: x = Acos(ωt + φ); với ω = √(k/m) 20 rad/s

Từ VTCB x = A và buông nhẹ ⇒ A = 2,5 cm

Câu 28: Một con lắc lò xo treo thẳng đứng. Kíck thích dao động đều hòa theo phương thẳng đứng. Chu kì và biên độ của con lắc lần lượt là 0,4 s và 8 cm. Chọn trục x’x phương thẳng đứng. Chiều dương hướng lên trên, gốc tọa độ tại VTCB, gốc thời gian t = 0 khi lực đàn hồi của lò xo cực tiểu và cđ theo chiều trục tọa độ. Lấy g = π² = 10 m/s². Thời gian ngắn nhất kể từ t = 0 đến khi lực đàn hồi cực đại là

A. 4/15 s        B. 2/15 s         C. 7/15 s        D. 11/15 s

Câu 29: Con lắc lò xo treo vào giá cố định, khối lượng vật nặng là m = 100g. Con lắc dao động điều hoà theo phương trình x = cos (10√5t) cm. Lấy g = 10 m/s². Lực đàn hồi cực đại và cực tiểu tác dụng lên giá treo có giá trị là

A. F_max = 1,5 N; F_min = 0,5 N

B. F_max = 1,5 N; F_min = 0 N

C. F_max = 2 N; F_min = 0,5 N

D. F_max = 1 N; F_min = 0 N.

Lời giải:

Chọn A.

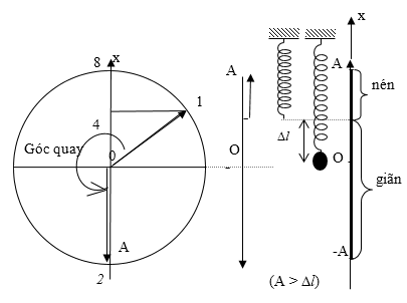
T = 0,4 s ⇒ ω = 5π rad/s. Tại VTCB: kΔl = mg ⇒ k/m = g/Δl ⇔ ω² = g/Δl

Tính được Δl = 4 cm

Góc quay hình vẽ (từ lúc t = 0 thì x₀ = 4 cm đến lúc lực đàn hồi cực đại x = – A): π + π/3 = 4π/3

Suy ra thời gian quay:

Đó là thời gian ngắn nhất kể từ t = 0 đến khi lực đàn hồi cực đại là 4/15 s

Câu 30: Con lắc lò xo treo thẳng đứng, dao động điều hòa với phương trình x = 2cos20t (cm). Chiều dài tự nhiên của lò xo là l₀ = 30 cm, lấy g = 10 m/s². Chiều dài nhỏ nhất và lớn nhất của lò xo trong quá trình dao động lần lượt là

A. 28,5 cm và 33 cm

B. 31 cm và 36 cm

C. 30,5 cm và 34,5 cm

D. 32 cm và 34 cm

Lời giải:

Chọn C.

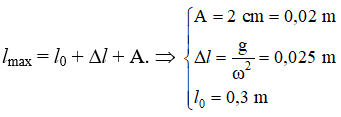
⇒ l_max = l₀ + Δl + A = 0,3 + 0,025 + 0,02 = 0,345 m = 34,5 cm

l_min = l₀ + Δl – A = 0,3 + 0,025 + 0,02 = 0,305 m = 30,5 cm

Câu 31: Một con lắc lò xo dao động điều hoà theo phương ngang với năng lượng dao dộng là 1 J và lực đàn hồi cực đại là 10 N. I là đầu cố định của lò xo. Khoảng thời gian ngắn nhất giữa 2 lần liên tiếp điểm I chịu tác dụng của lực kéo là 5√3 N là 0,1s. Quãng đường dài nhất mà vật đi được trong 0,4 s là :

A. 60 cm        B. 64 cm         C.115 cm         D. 84 cm

Lời giải:

Chọn A

Cách giải 1: Cơ năng : W = (1/2)k.A² .

Lực đàn hồi cực đại của con lắc dđ trên mặt phẳng ngang: F = kA.

Suy ra: k = 50 N/m, A = 0,2 m. Lực kéo: F = kx

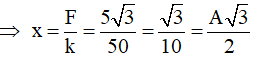
Đây là vị trí đặc biệt suy ra khoảng thời gian điểm I bị kéo là T/6 = 0,1 s ⇒ T = 0,6 s.

Suy ra 0,4 = 2T/3 = T/2 + T/6. Quãng đường đi được lớn nhất là

2A + A = 3A = 60 cm

Cách giải 2: (1/2)k.A² = 1 J ; kA = 10 N ⇒ A = 0,2 m = 20 cm.

Khi lực kéo bằng F = kx = 5√3 N

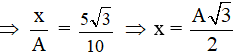
khoảng thời gian ngắn nhất giữa 2 lần liên tiếp vật qua li độ x = (A√3)/2 là

t = T/6 = 0,1 s ⇒ T = 0,6 s.

Quãng đường lớn nhất mà vật đi được trong 0,4 s = 2T/3 bằng quãng đường vật đi được trong một chu kỳ trừ đi quãng nhỏ nhất vật đi được trong một phần ba chu kì là A = A/2 + A/2. Suy ra S_max = 4A – A = 3A = 60 cm

Câu 32: Một con lắc lò xo treo thẳng đứng được kích thích cho dao động điều hòa. Thời gian quả cầu đi từ vị trí cao nhất đến vị trí thấp nhất là 1,5 s và tỉ số giữa độ lớn của lực đàn hồi lò xo và trọng lượng quả cầu gắn ở đầu con lắc khi nó ở vị trí thấp nhất là 76/75. Lấy gia tốc rơi tự do là g = π² m/s². Biên độ dao động là:

A. 5 cm         B. 3 cm         C. 4 cm         D. 2 cm

Lời giải:

Chọn D.

Dễ thấy T = 2t = 2.1,5 = 3s, ω = 2π/T = 2π/3 rad/s, k = mω², mg = kΔl

Theo bài ta có:

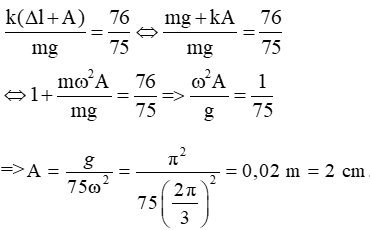
Câu 33: Một con lắc lò xo có độ cứng k = 100 N/m dao động điều hòa phương trình x = Acos(ωt + φ) . Biểu thức thế năng là: E_t = 0,1cos(4πt + π/2) + 1 J. Phương trình li độ là:

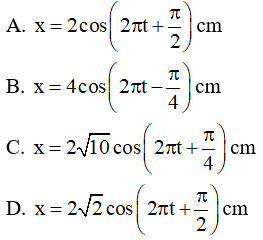
Lời giải:

Chọn C.

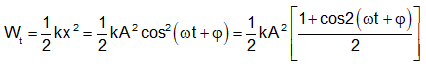
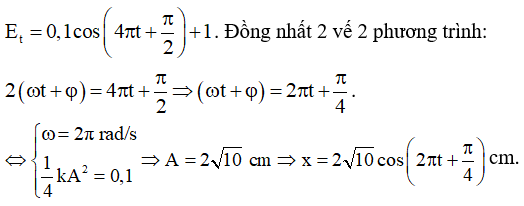
Câu 34: Một con lắc lò xo treo thẳng đứng có độ cứng 10 N/m, vật có khối lượng 25 g, lấy g = 10 m/s². Ban đầu người ta nâng vật lên sao cho lò xo không biến dạng rồi thả nhẹ cho vật dao động, chọn gốc thời gian lúc vật bắt đầu dao động, trục ox thẳng đứng chiều dương hướng xuống. Động năng và thế năng của vật bằng nhau vào những thời điểm là:

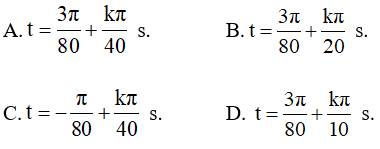
Lời giải:

Chọn C.

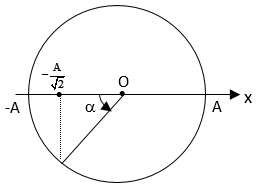
Câu 35: Con lắc lò xo nằm ngang, gồm lò xo có độ cứng k = 100 N/m, vật nặng khối lượng 100 g, được tích điện q = 2.10^-5 C (cách điện với lò xo, lò xo không tích điện). Hệ được đặt trong điện trường đều có E→ nằm ngang (E = 10⁵ V/m). Bỏ qua mọi ma sát, lấy π² = 10. Ban đầu kéo lò xo đến vị trí dãn 6 cm rồi buông cho nó dao động điều hòa (t = 0). Xác định thời điểm vật đi qua vị trí lò xo không biến dạng lần thứ 2013?

A. 201,30 s        B. 402,46 s        C. 201,27 s        D. 402,50 s

Lời giải:

Chọn C.

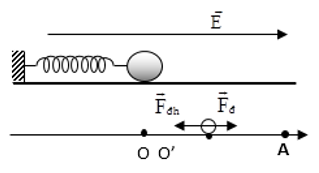
Chu kỳ T = 0,2 s. Vật m tích điện q > 0 dao động ngang trong điện trường chịu thêm F_n→ không đổi giống trường hợp treo thẳng đứng.

Phương trình ĐL II Newton cho vật m khi cân bằng ở VTCB mới O’: F_nh→ + F_n→ = 0

Chiếu lên chiều + ta có: – F_đh + F_đ = 0

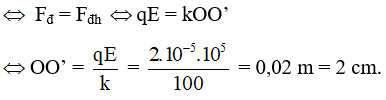
Ta có OA = 6 cm ⇒ O’A = 6 – 2 = 4 cm.

Biên độ dao động của vật trên trục O’x là A’ = O’A = 4 cm (vì buông v = 0). Thời điểm vật qua vị trí lò xo không biến dạng lần thứ nhất là vị trí O (có li độ – 2 cm) so với O’ là t₁ = T/4 + T/12 = T/3 = 2/30 s

Thời điểm vật qua vị trí lò xo không biến dạng lần thứ 2013 là :

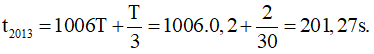
Câu 36: Một con lắc lò xo gồm quả cầu nhỏ m mang điện tích q = + 5.10^-5 C và lò xo có độ cứng k = 10 N/m, dao động điều hòa với biên độ 5 cm trên mặt phẳng nằm ngang không ma sát. Tại thời điểm quả cầu đi qua vị trí cân bằng và có vận tốc hướng ra xa điểm gắn lò xo với giá nằm ngang, người ta bật một điện trường đều có cường độ E = 10⁴ V/m, cùng hướng với vận tốc của vật. Tỉ số tốc độ dao động cực đại của quả cầu sau khi có điện trường và tốc độ dao động cực đại của quả cầu trước khi có điện trường bằng

A. 2        B. √3         C. √2        D. 3

Lời giải:

Chọn C. Tốc độ tại vị trí cân bằng cũ là: v = ωA. Vị trí cân bằng mới cách VTCB cũ một đoạn:

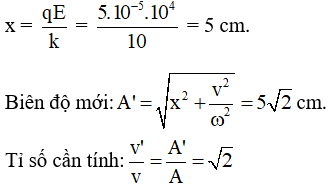
Câu 37: Một con lắc lò xo nằm ngang trên mặt bàn nhẵn cách điện gồm vật nặng tích điện q = 100 μC, lò xo có độ cứng k = 100 N/m. trong một điện trường đều E có hướng dọc theo trục lò xo theo chiều lò xo giãn Từ VTCB kéo vật một đoạn 6 cm rồi thả nhẹ, vật dao động điều hòa, Tốc độ khi qua VTCN là 1,2 m/s. Độ lớn cường độ điện trường E là 2,5.10⁴ V/m. Thời điểm vật qua vị trí có F_đh = 0,5 N lần thứ 2

A. π/10 s         B. π/30        C. π/20        D. π/5

Lời giải:

Chọn B

Tại VTCB lò xo giãn Δl_o = qE/k = 2,5.10^-2 m = 2,5 cm

Vậy khi F_nh→ = 0,5 N ⇒ |Δl| = 0,5.10^-2m = 0,5 cm. Khi đó vật có li độ là x = – 3 cm và x = – 2 cm

Thời điểm ban đầu của vât là t = 0 khi ở VTCB x = A = 6 cm nên vật qua VT lò xo giãn lần 2 tại VT x = – 3 cm. Khi đó góc quét là 2π/3 và thời điểm là t = φ/ω = 2π/ (3.20) = π/30 s

Câu 38: Lò xo nhẹ có độ cứng k, một đầu treo vào điểm cố định, đầu còn lại gắn với quả nặng có khối lượng m. Khi m ở vị trí cân bằng thì lò xo bị dãn một đoạn Δl. Kích thích cho quả nặng dao động điều hòa theo phương thẳng đứng xung quanh vị trí cân bằng của nó với chu kì T. Xét trong một chu kì dao động thì thời gian mà độ lớn gia tốc của quả nặng lớn hơn gia tốc rơi tự do g tại nơi treo con lắc là 2T/3. Biên độ dao động A của quả nặng m là

A. Δl/2         B. √2Δl         C. 2Δl        D. √3Δl

Lời giải:

Chọn C.

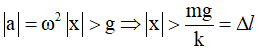
Vậy thời gian mà độ lớn gia tốc lớn hơn g là thời gian vật đi từ biên A đến Δl và ngược lại và từ – Δl đến – A và ngược lại. Thời gian vật đi từ biên A đến Δl:

Δt = Δφ/ω suy ra thời gian vật đi trong một chu kì là:

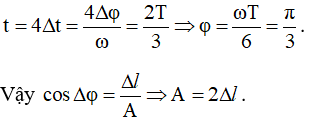
Câu 39: Một con lắc lò xo nằm ngang có vật nhỏ khối lượng m, dao động điều hoà với biên độ A. Khi vật đến vị trí có động năng bằng 3 lần thế năng thì một vật khác m' (cùng khối lượng với vật m) rơi thẳng đứng và dính chặt vào vật m thì khi đó 2 vật tiếp tục dao động điều hoà với biên độ

Lời giải:

Chọn B. Khi vật đến vị trí có động năng bằng 3 lần thế năng tức x = A/2. Lúc này vận tốc của vật 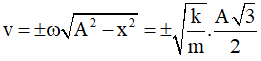thì va chạm mềm với vật m’

Áp dụng đinh luật bảo toàn động lượng theo phương ngang

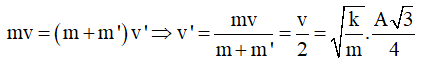
Áp dụng công thức độc lập

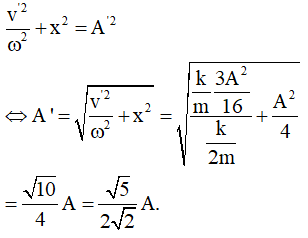
Câu 40: Một con lắc lò xo có độ cứng k = 40 N/m đầu trên được giữ cố định còn phia dưới gắn vật m. Nâng m lên đến vị trí lò xo không biến dạng rồi thả nhẹ vật dao động điều hòa theo phương thẳng đứng với biên độ 2,5 cm. Lấy g = 10 m/s² .Trong quá trình dao động, trọng lực của m có công suất tức thời cực đại bằng

A. 0,41 W        B. 0,64 W        C. 0,5 W         D. 0,32 W

Lời giải:

Chọn C. Công suất tức thời của trọng lực P = mgv với v là vận tốc của vật m:

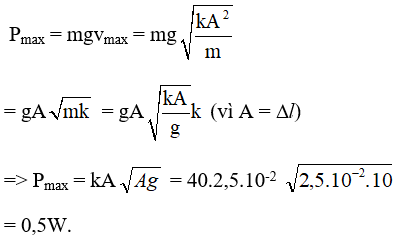
Câu 41: Một con lắc lò xo treo thẳng đứng đang dao động tự do. Biết khoảng thời gian mỗi lần diễn ra lò xo bị nén và véc tơ vận tốc, gia tốc cùng chiều bằng 0,05π s. Lấy g = π² = 10. Vận tốc cực đại bằng

A. 20 cm/s        B. √2 m/s        C. 10 cm/s        D. 10√2 cm/s

Lời giải:

Chọn B. Trong dao động điều hòa khoảng thời gian t diễn ra vec tơ vận tốc và gia tốc cùng chiều ứng với khoảng thời gian vật chuyển động từ biên đến VTCB tức là từ biện âm (– A) đến gốc O hoặc từ biên dương A đến gốc O và t = T/4. Do vậy ta có T/4 = 0,05π ⇒ T = 0,2π ⇒ ω = 10 rad/s. Khoảng thời gian lò xo bị nén bằng t = T/4 nên thời gian vật chuyển động từ li độ x = – Δl đến biên x = – A là t₁ = t/2 = T/8, Thời gian vật đi từ gốc tọa độ đến li độ x = – Δl là T/4 – T/8 = T/8 nên Δl = (A√2)/2 với A là biên độ của dao động

Mặt khác Δl = mg/k = g/(ω²) = 0,1 m = 10 cm.

⇒ Biên độ dao động

Vận tốc cực đại của vật treo v = ωA = 100√2 cm/s = 1,414 m/s.

Câu 42: Một con lắc lò xo gồm vật nặng khối lượng m và lò xo có độ cứng k dao động điều hòa theo phương thẳng đứng với tần số góc 5π rad/s ở nơi có gia tốc trọng trường g = 10 m/s²; lấy π² = 10. Biết gia tốc cực đại của vật nặng a_max > g. Trong thời gian một chu kì dao động, thời gian lực đàn hồi của lò xo và lực kéo về tác dụng vào vật cùng hướng là t₁, thời gian 2 lực đó ngược hướng là t₂. Cho t₁ = 5t₂. Trong một chu kì dao động, thời gian lò xo bị nén là :

A. 1/15 s        B. 2/3 s        C. 2/15 s         D. 1/30 s

Lời giải:

Chọn C.

Chu kì dao động của con lắc: T = 0,4 s. Xét trong một chu kì dao động: Thời gian lực đàn hồi của lò xo và lực kéo về tác dụng vào vật cùng hướng là tổng thời gia lò xo bị nén t_n và thời gian lò xo bị giãn ở dưới VTCB T/2

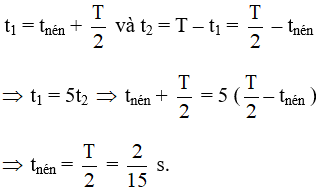
Câu 43: Một con lắc lò xo có khối lượng quả nặng là m, lò xo có độ cứng k, đang cân bằng trên mặt phẳng nghiêng một góc 37° so với mặt phẳng ngang (sin7° = 0,6). Gọi Δl là độ dãn của lò xo khi vật ở vị trí cân bằng. Tăng góc nghiệng thêm 16°, khi vật ở vị trí cân bằng thì lò xo dài thêm 2cm. Bỏ qua ma sát, lấy g = 10 m/s². Tần số dao động riêng của con lắc là:

A. 12,5 rad/s        B. 10 rad/s         C. 15 rad/s         D. 5 rad/s

Lời giải:

Chọn B

Mặt phẳng nghiêng: sinα = sin37° = (F/P).0,6 = (k.Δl)/m.g     (1)

Tăng góc nghiêng:

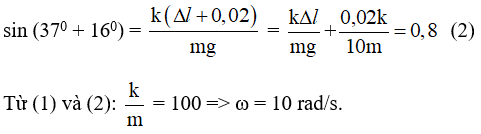
Câu 44: Một lò xo nhẹ, dài tự nhiên 20 cm, dãn ra 1 cm dưới tác dụng của lực kéo 0,1 N. Đầu trên của lò xo gắn vào điểm O, đầu dưới treo vật nặng 10 g. Hệ đang đứng yên. Quay lò xo quanh trục thẳng đứng qua O với một tốc độ góc không đổi, thì thấy trục lò xo làm với phương thẳng đứng góc 60°. Lấy g = 10 m/s². Chiều dài của lò xo và tốc độ quay xấp xỉ bằng

A. 20 cm; 15 vòng/s

B. 22 cm; 15 vòng/s

C. 20 cm; 1,5 vòng/s

D. 22 cm; 1,5 vòng/s

Lời giải:

Chọn D

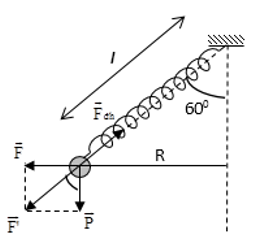
Vì F là lực ly tâm : F = mω²R = Ptan60°

mω²l.cos60° = Ptan60°

ω = 9,53 rad/s = 1,5 vòng/s.

Câu 45: Một con lắc lò xo dao động điều hòa trên mặt phẳng nằm ngang với chu kỳ T = 2π s, quả cầu nhỏ có khối lượng m₁. Khi lò xo có độ dài cực đại và vật m₁ có gia tốc là – 2 cm/s² thì một vật có khối lượng m₂ (m₁ = 2m₂) chuyển động dọc theo trục của lò xo đến va chạm đàn hồi xuyên tâm với vật m₁, có hướng làm lò xo nén lại. Biết tốc độ chuyển động của vật m₂ ngay trước lúc va chạm là 3 cm/s. Quãng đường mà vật m₁ đi được từ lúc va chạm đến khi vật m₁ đổi chiều chuyển động là

A. 6 cm        B. 6,5 cm        C. 2 cm        D. 4 cm

Lời giải:

Chọn D.

Tần số góc ω = 1 rad/s.

Tại vị trí va chạm thì li độ bằng biên cũ: x = A = (|a_max|)/(ω²) = 2 cm

Trước va chạm vật m1 có vận tốc bằng không. Bảo toàn động lượng cho ta:

m₂v = m₁v₁ – m₂v₂     (1)

Bảo toàn năng lượng theo phương ngang ta có:

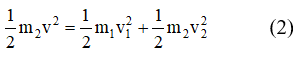
Từ (1) và (2) và m₁ = 2m₂ ta có v₁ = 2 cm.

Biên mới:

Câu 46 Một lò xo nhẹ có độ cứng k, một đầu treo vào một vào một điểm cố định, đầu dưới treo vật nặng 100g. Kéo vật nặng xuống dưới theo phương thẳng đứng rồi thả nhẹ. Vật dao động điều hòa theo phương trình: x = 5cos4πt cm lấy g = 10 m/s² và π² = 10. Lực dùng để kéo vật trước khi dao động có độ lớn

A 0,8 N        B 1,6 N         C 6,4 N         D 3,2 N

Lời giải:

Chọn A.

Thay t = 0 vào PT dao động của vật có x = 5 cm ⇒ Tức là người ta đã kéo vật đến vị trí x = 5 cm (Xuống dưới VTCB 5cm) rồi thả nhẹ.

Mặt khác tại VTCB lò xo giãn Δl = mg/k = g/ω² = 0,0625 m

⇒ Tại vị trí mà người ta giữ vật (x = 5 cm) lò xo giãn Δl = Δl_o + x = 0,0625 + 0,05 = 0,1125 m

⇒ Lực mà người ta giữ bằng F_đh của lò xo.

Trọng lực P = kΔl = mω²Δl = 0,8 N (Vì trọng lực góp phần kéo vật xuống)

Câu 47: Hai con lắc lò xo giống nhau có khối lượng vật nặng 10g, độ cứng lò xo là 100π² N/m dao động điều hòa dọc theo hai đường thẳng song song kề liền nhau (vị trí cân bằng hai vật đều ở gốc tọa độ). Biên độ của con lắc dao động thứ nhất lớn gấp đôi con lắc thứ hai. Biết rằng hai vật gặp nhau khi chúng chuyển động ngược chiều nhau, Khoảng thời gian giữa ba lần hai vật nặng gặp nhau liên tiếp là:

A. 0,03 s         B. 0,02 s        C. 0,04 s        D. 0,01 s

Lời giải:

Chọn B. Chu kỳ của mỗi con lắc là

Nhận xét: Giả sử 2 vật lúc đầu gặp nhau tại li độ x₀ tức là x₁ = x₂ = x₀, sao đó nửa chu kỳ thì x₁ = – x₀ và x₂ = – x₀ ⇒ x₁ = x₂ = – x₀ chúng lại gặp nhau ở vị trí đối xứng qua gốc O ⇒ Cứ sau mỗi T/2 chúng lại gặp nhau.

Khoảng thời gian giữa 3 lần liên tiếp gặp nhau = 2 khoảng thời gian trên = 2.(T/2) = 0,02 s.

Câu 48: Hai con lắc lò xo nằm ngang có chu kì T₁ = T₂/2. Kéo lệch các vật nặng tới vị trí cách các vị trí cân bằng của chúng một đoạn A như nhau và đồng thời thả cho chuyển động không vận tốc đầu. Khi khoảng cách từ vật nặng của con lắc đến vị trí cân bằng của chúng đều là b (0 < b < A) thì tỉ số độ lớn vận tốc của các vật nặng là:

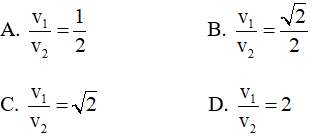
Lời giải:

Chọn D. Biên độ của cả 2 con lắc là A₁ = A₂ = A vì cùng kéo lệch các vật nặng tới vị trí cách các vị trí cân bằng của chúng một đoạn A như nhau và đồng thời thả nhẹ.

Khoảng cách đến vị trí cân bằng là |x|. Khi khoảng cách từ vật nặng của con lắc đến vị trí cân bằng của chúng đều là b (0 < b < A) tức là |x₁| = |x₂| = b

Từ công thức độc lập thời gian có

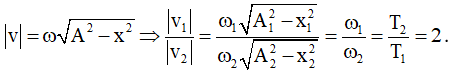
Câu 50: Một con lắc lò xo nằm ngang gồm vật nặng tích điện q = 20 μC và lò xo có độ cứng k = 10 N/m. Khi vật đang nằm cân bằng, cách điện, trên mặt bàn nhẵn thì xuất hiện tức thời một điện trường đều trong không gian bao quanh có hướng dọc theo trục lò xo. Sau đó con lắc dao động trên một đoạn thẳng dài 4 cm. Độ lớn cường độ điện trường E là:

A. 2.10⁴ V/m.         B. 2,5.10⁴ V/m.        C. 1,5.10⁴ V/m.         D. 10⁴ V/m.

Lời giải:

Chọn D. Cách giải 1: Vì chiều dài đoạn thẳng dao động là 4 cm suy ra biên độ A = 2 cm. Khi vật m dao động hợp của lực điện trường và lực đàn hồi gây gia tốc a cho vật. Tại vị trí biên, vật có gia tốc lớn nhất. Khi đó ta có:

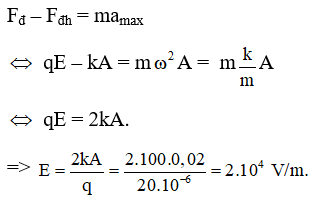
Cách giải 2: Ta tưởng tượng đây là con lắc treo thẳng đứng với lực điện đóng vai trò như trọng lực. Ban đầu đưa vật lên vị trí lò xo không biến dạng rồi buông nhẹ, như vậy Δl = A = 2 cm. Tại vị trí cân bằng ta có: F_đh = F_đ ⇔ kΔl = qE.

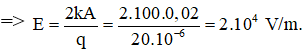
Câu 51: Một vật nặng có khối lượng m, điện tích q = +5.10^-5 được gắn vào lò xo có độ cứng k = 10 N/m tạo thành con lắc lò xo nằm ngang. Điện tích trên vật nặng không thay đổi khi con lắc dao động và bỏ qua mọi ma sát. Kích thích cho con lắc dao động điều hòa với biên độ 5 cm. Tại thời điểm vật nặng đi qua vị trí cân bằng và có vận tốc hướng ra xa điểm treo lò xo, người ta bật một điện trường đều có cường độ E = 10⁴ V/m, cùng hướng với vận tốc của vật. Khi đó biên độ dao động mới của con lắc lò xo là:

A. 10 cm.        B. 7,07 cm.        C. 5 cm.        D. 8,66 cm.

Lời giải:

Chọn B. Động năng của vật khi đi qua vị trí cân bằng (khi chưa có điện trường):

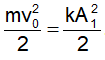
Vị trí cân bằng mới (khi có thêm điện trường) lò xo biến dạng một đoạn: Δl = qE/k = 0,05 m = 5 cm

Ở thời điểm bắt đầu có điện trường có thể xem đưa vật đến vị trí lò xo có độ biến dạng Δl và truyền cho vật vận tốc v₀. Vậy năng lượng mới của hệ là:

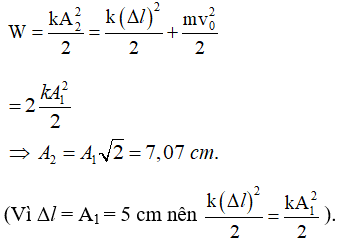
Câu 52: Một con lắc lò xo dao động điều hoà theo phương thẳng đứng tại nơi có gia tốc trọng trường g. Đưa con lắc này lên thang máy đang chuyển động nhanh dần đều hướng lên với gia tốc a = g/10. So với thang máy khi đứng yên, độ dãn của lò xo ở vị trí cân bằng sẽ:

A. tăng 10%.         B. giảm 20%.        C. tăng 1%.          D. không thay đổi.

Lời giải:

Chọn B. Độ dãn của con lắc lò xo tại nơi có gia tốc trọng trường g: Δl = mg/k     (1)

Độ dãn của con lắc này lên thang máy đang chuyển động nhanh dần đều hướng lên với gia tốc

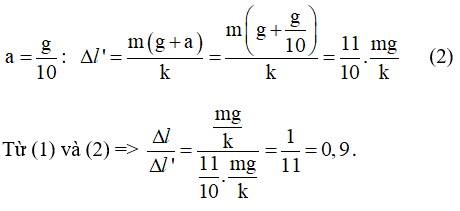
Vậy so với thang máy khi đứng yên, độ dãn của lò xo ở vị trí cân bằng sẽ tăng 1%

Câu 53: Một con lắc lò xo nằm ngang gồm vật m = 100 g nối với lò xo có độ cứng k = 100 N/m, đầu kia lò xo gắn vào điểm cố định. Từ vị trí cân bằng đẩy vật sao cho lò xo nén 2 cm rồi buông nhẹ. Khi vật đi qua vị trí cân bằng lần đầu tiên thì tác dụng lên vật lực F→ không đổi cùng chiều vận tốc có độ lớn F = 2N. Khi đó vật dao động điều hòa với biên độ A₁. Sau thời gian 1/30 s kể từ khi tác dụng lực F→, ngừng tác dụng lực F→ . Khi đó vật dao động điều hòa với biên độ A₂. Biết trong quá trình sau đó lò xo luôn nằm trong giới hạn đàn hồi. Bỏ qua ma sát giữa vật và sàn. Tỉ số A₂/A₁ bằng

A. √7/2         B. 2         C. √14        D. 2√7

Lời giải:

Chọn D.

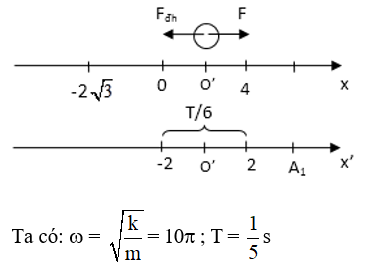
Sau khi buông vật, vật qua VTCB với vận tốc :

V₀ = ωA = 10π.2√3 = 20π√3 cm/s

Tác dụng lên vật lực F→, VTCB mới của vật là O’ (là nơi F và F_đh cân bằng):

kx₀ = F ⇒ x₀ = 0,02m = 2cm = OO’

Với trục toa độ Ox’, gốc tọa độ O’, vật ở VT O có:

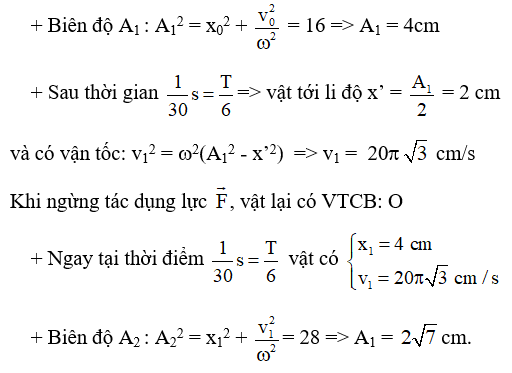
Câu 54: Một con lắc lò xo gồm lò xo có độ cứng k = 2 N/m, vật nhỏ khối lượng m = 80 g, dao động trên mặt phẳng nằm ngang, hệ số ma sát trượt giữa vật và mặt phẳng ngang là μ = 0,1. Ban đầu kéo vật ra khỏi vị trí cân bằng một đoạn 10 cm rồi thả nhẹ. Cho gia tốc trọng trường g = 10 m/s². Tốc độ lớn nhất mà vật đạt được bằng:

A. 0,36 m/s         B. 0,25 m/s          C. 0,50 m/s         D. 0,30 m/s

Lời giải:

Chọn D

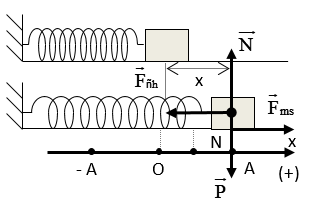
Vật có tốc độ cực đại khi gia tốc bằng 0; tức là lúc 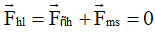lần đầu tiên tại N: ON = x ⇒ kx = μmg ⇒ x = μmg/k = 0,04 m = 4 cm

Khi đó vật đã đi được quãng đường

S = MN = 10 – 4 = 6 cm = 0,06 m

Theo ĐL bảo toàn năng lượng ta có:

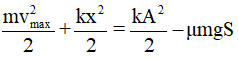
(Công của lực ma sát F_ms = μmgS)

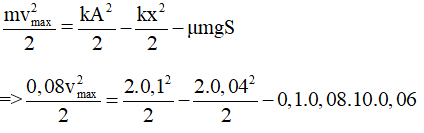
= 0,0036

⇒ (v_max)² ⇒ v_max = 0,3 m/s = 30 cm/s

Câu 55: Một con lắc lò xo gồm một vật nhỏ khối lượng 0,02 kg và lò xo có độ cứng 1 N/m. Vật nhỏ được đặt trên giá đỡ cố định nằm ngang dọc theo trục lò xo. Hệ số ma sát trượt của giá đỡ và vật nhỏ là 0,1. Ban đầu giữ vật ở vị trí lò xo bị nén 10 cm rồi buông nhẹ để con lắc dao động tắt dần. Lấy g = 10 m/s². Tốc độ lớn nhất vật nhỏ đạt được trong quá trình dao động là

A. 40√3 cm/s

B. 20√6 cm/s

C. 10√30 cm/s

D. 40√2 cm/s

Lời giải:

Chọn D. Vì cơ năng của con lắc giảm dần nên vận tốc của vật sẽ có giá trị lớn nhất tại vị trí nằm trong đoạn đường từ lúc thả vật đến lúc vật qua VTCB lần thứ nhất (0 ≤ x ≤ A):

Tính từ lúc thả vật (cơ năng (1/2)kA²) đến vị trí bất kỳ có li độ x (0 ≤ x ≤ A) và có vận tốc v (cơ năng (1/2)mv² + (1/2)kx² ) thì quãng đường đi được là (A – x)

Độ giảm cơ năng của con lắc:

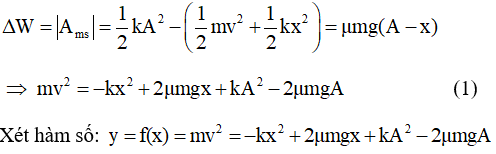
Dễ thấy rằng đồ thị hàm số y = f(x) có dạng là parabol, bề lõm quay xuống dưới (a = – k < 0), như vậy y = mv² có giá trị cực đại tại vị trí x = -b/2a = μmg/k = 0,02 m

Thay x = 0,02 m vào (1) ta tính được v_max = 40√2 cm/s

Câu 56: Cho hai vật nhỏ A và B có khối lượng lần lượt là m₁ = 900 g, m₂ = 4 kg đặt trên mặt phẳng nằm ngang. Hệ số ma sát trượt giữa A, B và mặt phẳng ngang đều là μ = 0,1; coi hệ số ma sát nghỉ cực đại bằng hệ số ma sát trượt. Hai vật được nối với nhau bằng một lò xo nhẹ có độ cứng k = 15 N/m; B tựa vào tường thẳng đứng. Ban đầu hai vật nằm yên và lò xo không biến dạng. Vật nhỏ C có khối lượng m = 100 g bay dọc theo trục của lò xo với vận tốc v→ đến va chạm hoàn toàn mềm với A (sau va chạm C dính liền với A). Bỏ qua thời gian va chạm. Lấy g = 10 m/s². Giá trị nhỏ nhất của v để B có thể dịch chuyển sang trái là

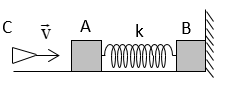
A. 1,8 m/s         B. 18 m/s          C. 9 m/s          D. 18 cm/s

Lời giải:

Chọn B. Để B có thể dịch sang trái thì lò xo phải giãn một đoạn ít nhất là x_o sao cho:

F_đh = F_ms ⇒ kx_o = μm₂g ⇒ 150x_o = 40 ⇒ x_o = 4/15 m

Như thế, vận tốc v_o mà hệ (m₁ + m) có khi bắt đầu chuyển động phải làm cho lò xo có độ co tối đa x sao cho khi nó dãn ra thì độ dãn tối thiểu phải là x_o.

Suy ra:

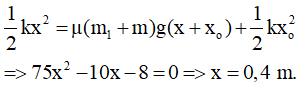
Theo định luật bảo toàn năng lượng ta có:

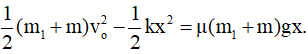
Từ đó tính được: v_o  min ≈ 1,8 m/s ⇒ v_min ≈ 18 m/s

Câu 57: Con lắc lò xo gồm vật nặng M = 300 g, lò xo có độ cứng k = 200 N/m lồng vào một trục thẳng đứng như hình bên. Khi M đang ở vị trí cân bằng, thả vật m = 200 g từ độ cao h = 3,75 cm so với M. Lấy g = 10 m/s². Bỏ qua ma sát. Va chạm là mềm. Sau va chạm cả hai vật cùng dao động điều hòa. Chọn trục tọa độ thẳng đứng hướng lên, gốc tọa độ là vị trí cân bằng của M trước khi va chạm, gốc thời gian là lúc va chạm. Phương trình dao động của hai vật là :

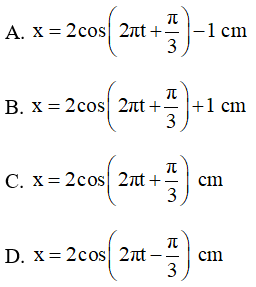
Lời giải:

Chọn A.

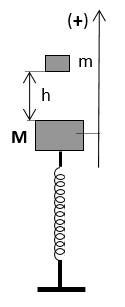
Chọn mốc thế năng tại O (Vị trí cân bằng của M trước va chạm)

Áp dụng định luật bảo toàn cơ năng cho m ta có :

mgh = 1/2(mv²) ⇒ v = √(2gh) ≈ 0,866 m/s

Khi có thêm vật m vị trí cân bằng mới O’ cách O một đoạn: Δl = mg/k = 1cm

Như vậy hệ (m + M ) sẽ dao động điều hòa quanh vị trí cân bằng O’ cách O một đoạn 1 cm. Phương trình dao động của hệ (m + M) khi gốc tọa độ tại O có dạng là: x = Acos(ωt + φ)-1 cm

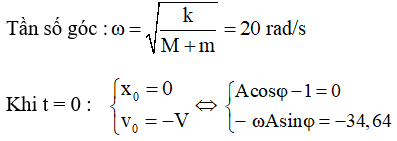
Giải hệ phương trình trên ta được: A = 2cm ; φ = π/3

Phương trình dao động là : x = 2cos(2πt + π/3) - 1 (cm)

Câu 58: Cho cơ hệ như hình bên. Biết M = 1,8 kg, lò xo nhẹ độ cứng k = 100 N/m. Một vật khối lượng m = 200g chuyển động với tốc độ v₀ = 5 m/s đến va vào M (ban đầu đứng yên) theo trục của lò xo. Hệ số ma sát trượt giữa M và mặt phẳng ngang là μ = 0,2. Coi va chạm hoàn toàn đàn hồi xuyên tâm. Tốc độ cực đại của M sau khi lò xo bị nén cực đại là:

A. 1 m/s        B. 0,8862 m/s        C. 0,4994 m/s         D. 0,4212 m/s

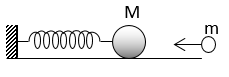
Lời giải:

Chọn C. Chọn gốc tọa độ là vị trí lò xo bị nén cực đại, chiều dương sang phải

ĐL bảo toàn động lượng:

mv₀→ = mv₁→ + Mv₂→ ⇒ mv_o = mv₁ + Mv₂     (1)

Động năng bảo toàn

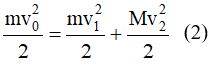
Từ (1), (2) có:

Định luật bảo toàn năng lượng:

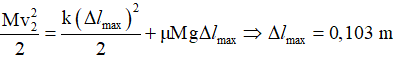
Tốc độ của M đạt cực đại tại vị trí có: F_đh = F_ms ⇒ μMg = kx ⇒ x = μMg/k = 0,036 m

Định luật bảo toàn năng lượng:

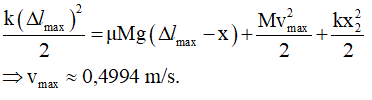
Câu 59: Một con lắc lò xo đặt nằm ngang gồm vật M có khối lượng 500 g dao động điều hòa với biên độ 8 cm. Khi M qua vị trí cân bằng người ta thả nhẹ vật m có khối lượng 300 g lên M (m dính chặt ngay vào M), sau đó hệ m và M dao động với biên độ

A. 2√5 cm.         B. 2√6 cm.        C. 3√6 cm.         D. 2√10 cm.

Lời giải:

Chọn D.

Do khi M qua vị trí cân bằng thì thả vật m dính lên nên để tìm biên độ của hệ M và m thì ta tìm vận tốc ngay sau khi thả của hệ. Từ đó ta tìm được biên độ của hệ. Cụ thể:

Áp dụng định luật bảo toàn động lượng (va chạm mềm), ta có:

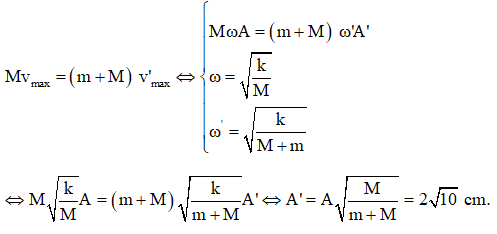
Câu 60: Cho cơ hệ như hình vẽ. Lò xo có độ cứng k = 100 N/m, m₁ = 100 g, m₂ = 150 g. Bỏ qua ma sát giữa m₁ và mặt sàn nằm ngang, ma sát giữa m₁ và m₂ là μ₁₂ = 0,8. Biên độ dao động của vật m₁ bằng bao nhiêu để hai vật không trượt lên nhau:

A. A ≤ 0,8 cm.        B. A ≤ 2 cm         C. A ≤ 7,5 cm         D. A ≤ 5cm

Lời giải:

Chọn C

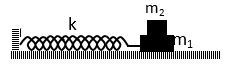
Để không trượt: Lực quán tính cực đại nhỏ hơn lực ma sát: