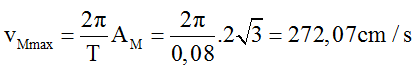Cách giải bài tập về đồ thị sóng dừng cực hay có lời giải - Vật Lí lớp 12
Cách giải bài tập về đồ thị sóng dừng cực hay có lời giải
Với Cách giải bài tập về đồ thị sóng dừng cực hay có lời giải Vật Lí lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập đồ thị sóng dừng từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

A. Phương pháp giải
I. Phương pháp:
1. Xác định các đại lượng đặc trưng, trạng thái chuyển động của các phần tử môi trường
a. Biên độ, chu kì sóng, bước sóng và các vị trí có biên độ dao động đặc biệt
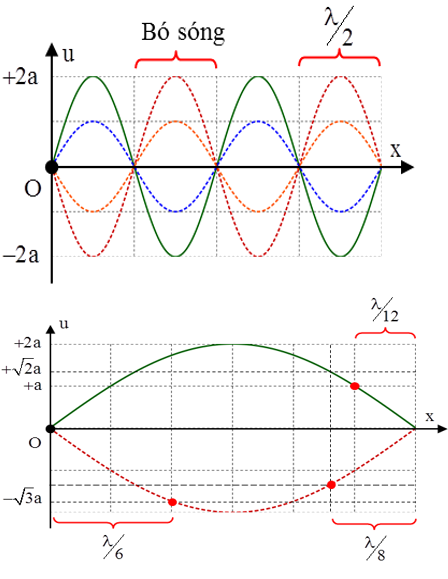
Khi xảy ra sóng dừng, biên độ dao động của các phần tử được xác định bởi
+ aM = 2a|sin2πd/λ| với d là khoảng các từ M đến nút bất kỳ.
+ aM = 2a|cos2πd/λ| với d là khoảng các từ M đến bụng bất kỳ.
b. Trạng thái chuyển động của các phần tử
Khi xảy ra sóng dừng, các phần tử đối xứng nhau qua một nút thì dao động ngược pha nhau, đối xứng nhau qua một bụng thì dao động cùng pha nhau.
B. Ví dụ minh họa
Ví dụ 1: (QG-2015): Trên một sợi dây OB căng ngang, hai đầu cố định đang có sóng dừng với tần số f xác định. Gọi M, N và P là ba điểm trên dây có vị trí cân bằng cách B lần lượt là 4 cm, 6 cm và 38 cm. Hình vẽ mô tả hình dạng sợi dây tại thời điểm t1 (đường 1) và t2 = t1 + 11/12f (đường 2). Tại thời điểm t1, li độ của phần tử dây ở N bằng biên độ của phần tử dây ở M và tốc độ của phần tử dây ở M là 60 cm/s. Tại thời điểm t2, vận tốc của phần tử dây ở P là
A. 60 cm/s. B. 20√3 cm/s. C. -20√3 cm/s. D. - 60 cm/s.
Hướng dẫn giải:
Chọn D
Theo hình vẽ ta có: λ = 24 cm.
Tính biên độ dao động của các điểm M, N, P: A = Ab|sin 2πx/λ|
(với Ab: biên độ của điểm bụng, x là khoảng cách từ điểm xét tới điểm nút bất kỳ).
Thay số, ta được: AM = Ab√3/2; AN = Ab; Ap = Ab/2
Dễ dàng thấy: N và M cùng pha, N và P ngược pha.
Tại thời điểm t1: li độ của điểm N bằng biên độ M thì tốc độ dao động của M bằng 60 cm/s:
(vì N và M cùng pha)
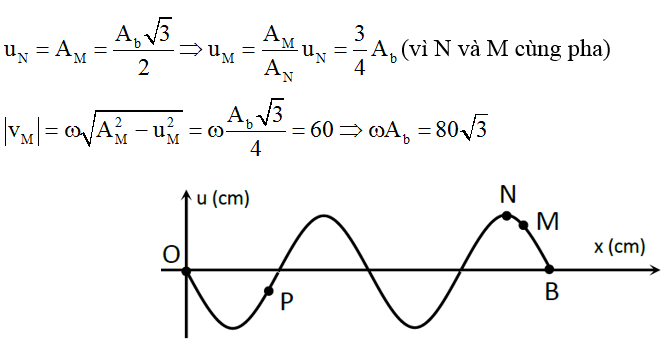
Tại thời điểm t2 (sau t1 là 11T/12 ) hình dạng sợi dây (đường 2) có dạng như hình vẽ trên.
Tại thời điểm t1 các phần tử M, N, P đang chuyển động theo chiều đi ra vị trí biên tương ứng. Vec tơ quay mô tả chuyển động của N, P tại thời điểm t1 và t2:
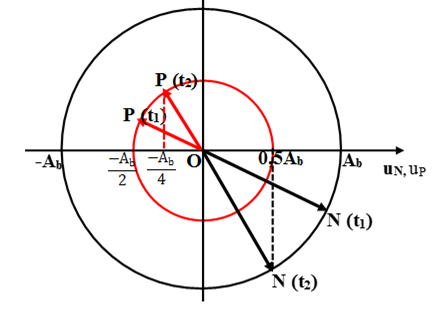
Vậy ở thời điểm t2, điểm P có li độ là up = -Ab/4 và P đang đi theo chiều âm.
Suy ra:
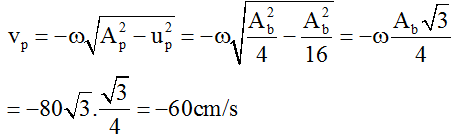
Ví dụ 2: Một sóng dừng trên một sợi dây đàn hồi có dạng u = 2A sin2πx/λcos(2π/T.t + π/2) , trong đó u là li độ tại thời điểm t của phần tử M trên sợi dây mà vị trí cân bằng của nó cách gốc tọa độ O một đoạn x. Ở hình vẽ, đường mô tả hình dạng của sợi dây tại thời điểm t1 là đường (1).
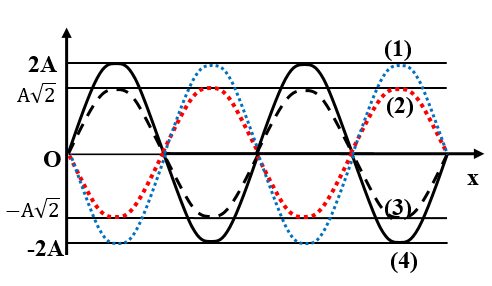
Tại các thời điểm t2 = t1 + 3T/8; t3 = t1 + 7T/8; t4 = t1 + 3T/2 hình dạng của sợi dây lần lượt là các đường:
A. (3), (4), (2) B. (3), (2), (4) C. (2), (4), (3) D. (2), (3), (4)
Hướng dẫn giải:
Chọn B
Ta lấy điểm K trên đường (1). Tại thời điểm t1, K đang ở biên âm.
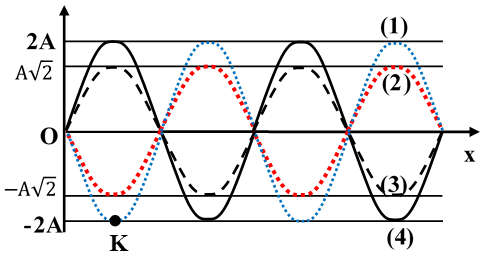
Sau t2 = t1 + 3T/8 , K ở li độ A√2 => đường (3).
Sau t3 = t1 + 7T/8 , K ở li độ -A√2 => đường (2).
Sau t4 = t1 + 3T/2, K ở li độ 2A => đường (4).
Vậy xếp theo thứ tự (3), (2), (4).
C. Bài tập vận dụng
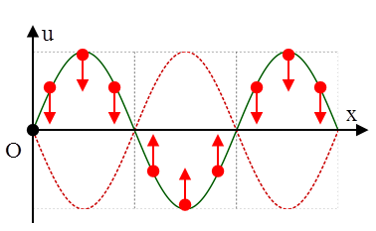
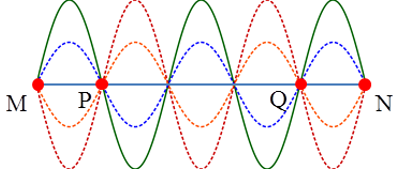
Câu 1: Hình ảnh dưới đây mô tả sóng dừng trên một sợi dây MN. Gọi H là một điểm trên dây nằm giữa hai nút M, P. Gọi K là một điểm trên dây nằm giữa hai nút Q và N. Kết luận nào sau đây là đúng?
A. H và K dao động lệch pha nhau π/5
B. H và K dao động ngược pha nhau.
C. H và K dao động lệch pha nhau π/2.
D. H và K dao động cùng nhau.
Lời giải:
Chọn D
Từ đồ thị sóng dừng ta nhận thấy hai điểm H và K lần lượt nằm trên đoạn chứa bó sóng số 1 và số 5 nên có thể coi chúng nằm đối xứng qua 1 bó (bó số 3), do vậy chúng sẽ dao động cùng pha với nhau.
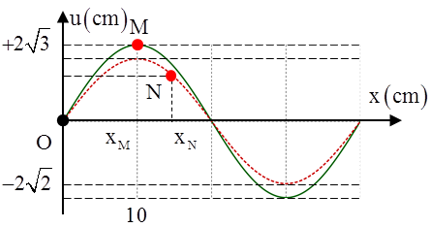
Câu 2: Sóng dừng trên một sợi dây với biên độ điểm bụng là 4 cm. Hình vẽ biểu diễn hình dạng của sợi dây ở thời điểm t1 (nét liền) và t2 (nét đứt). Ở thời điểm t1 điểm bụng M đang di chuyển với tốc độ bằng tốc độ của điểm N ở thời điểm t2. Tọa độ của điểm N ở thời điểm t2 là:
A. uN = 2cm; xN = 40/3cm
B. uN = √6 cm, xN = 15cm
C. uN = 2cm; xN = 15cm
D. uN = √6 cm, xN = 40/3cm
Lời giải:
Chọn C
Tại thời điểm t1, M có li độ uM1 = 2√3 cm. Tốc độ của M là:
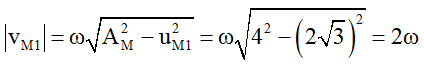
Tại thời điểm t2, M có li độ uM2 = 2√2 cm. Tốc độ của M là:
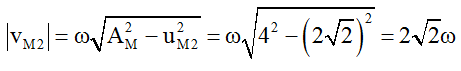
Vì M và N cùng nằm trong một bó nên dao động đồng pha, do vậy:
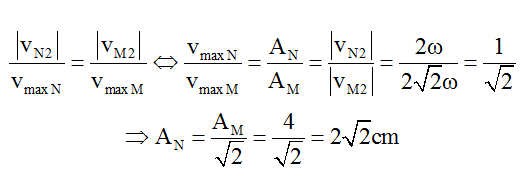
Mặt khác theo bài ra ta có: |vN2| = |vM1| = 2ω
Li độ của N tại thời điểm t2 là uN2 thỏa mãn hệ thức độc lập:
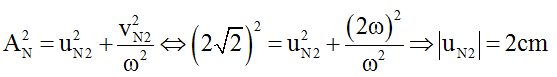
Biên độ sóng tại N được xác định bằng công thức: AN = Ab.|cos 2πxN/λ| (trong Ab là biên độ của bụng sóng, Ab = 4cm)
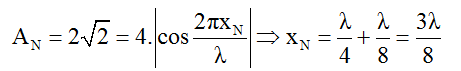
Từ đồ thị ta có: xM = λ/4 = 10cm → λ = 40cm → xN = 15cm
Vậy uN2 = 2cm; xN = 15cm.
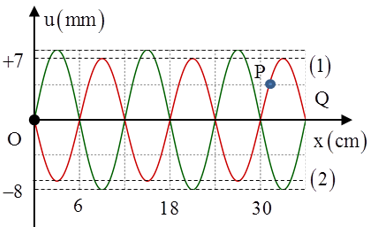
Câu 3: Trên sợi dây OQ căng ngang, hai đầu cố định đang có sóng dừng với tần số f xác định. Hình vẽ mô tả hình dạng sợi dây tại thời điểm t1 (đường 1), t2 = t1 + 1/6f (đường 2) và P là một phần tử trên dây. Tỉ số tốc độ truyền sóng trên dây và tốc độ dao động cực đại của phần tử P xấp xỉ bằng
A. 0,5. B. 2,6. C. 2,2. D. 4,8.
Lời giải:
Chọn C
Ta có: λ/2 = 6cm → λ = 12cm = 120mm
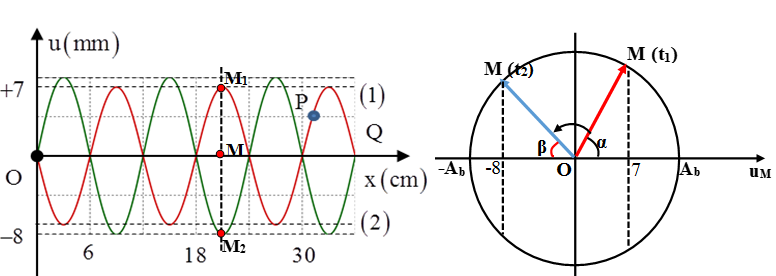
Xét phần tử bụng M trên sợi dây có VTCB như hình vẽ, thời điểm t1 có vị trí M1 (u1 = 7mm), đến thời điểm t2 có vị trí M2 (u2 = -8mm).
Sử dụng dụng vòng tròn lượng giác biểu diễn li độ uM, ta vẽ các vectơ quay tương ứng với hai thời điểm t1 và t2 với góc quét ∆φ = π/3 rad (do )
Từ hình vẽ ta có:
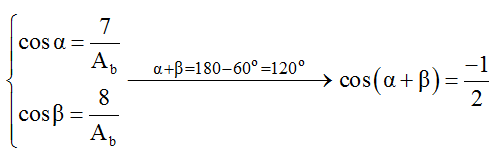
Khai triển lượng giác: cos(α + β) = cosα.cosβ – sinα.sinβ, kết hợp với cosα = √(1-sin2α ) , ta được:
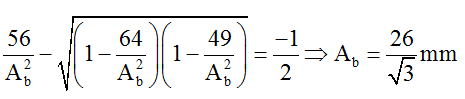
+ Từ đồ thị ta thấy: tại thời điểm t1, P có li độ 4 mm, điểm bụng gần nhất có li độ 7 mm, đồng thời P dao động đồng pha với bụng.
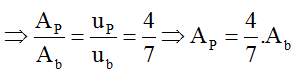
Suy ra tỉ số:
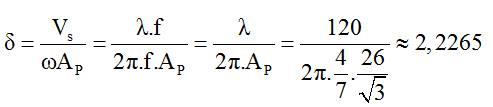
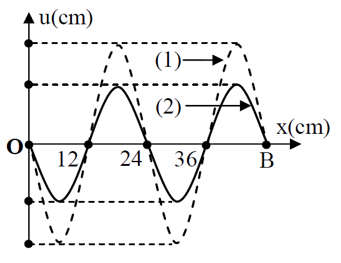
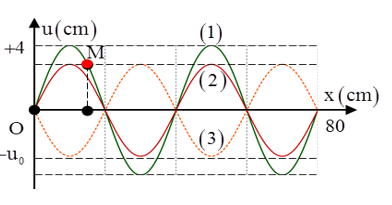
Câu 4: Sóng dừng trên một sợi dây đàn hồi OB mô tả như hình dưới. Điểm O trùng với gốc tọa độ trục tung. Lúc t = 0 hình ảnh của sợi dây là (1), sau thời gian nhỏ nhất ∆t và 3∆t kể từ lúc t = 0 thì hình ảnh của sợi dây lần lượt là (2) và (3). Tốc độ truyền sóng là 20 m/s và biên độ của bụng sóng là 4 cm. Sau thời gian 1/30 s kể từ lúc t = 0, tốc độ dao động của điểm M là:
A. 10,9 m/s B. 6,3 m/s C. 4,4 m/s D. 7,7 m/s
Lời giải:
Chọn D
Ta có: 2λ = 80cm → λ = 40cm
Xét 1 phần tử bụng B gần M nhất trên sợi dây, từ đồ thị ta thấy:
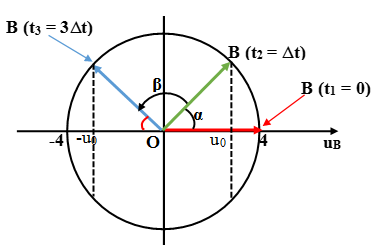
Tại thời điểm t = O, B ở biên dương uB1 = 4cm. Sau thời gian ngắn nhất t2 = ∆t, B có li độ uB2 = u0. Tại thời điểm t3 = 3∆t, B có li độ uB3 = - uo.
Sử dụng vòng tròn lượng giác ta có: β = ω.(t3 – t2) = ω.2∆t; α = ω.∆t → β = 2α
Mà β = 2(π/2 – α) = π - 2α → β = π/2; α = π/4
Suy ra 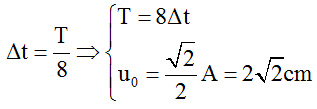
Chu kỳ sóng: T = λ/vs = 0,4/20 = 0,02s.
M dao động đồng pha với B nên tại thời điểm t = 0, B ở biên dương thì M cũng ở biên dương, do đó AM = 2√2 cm.
Khoảng thời gian t = 1/30s = T + 2T/3 thì M có li độ là uM = -AM/2 (dùng vòng tròn lượng giác).
Tốc độ của M khi đó là:
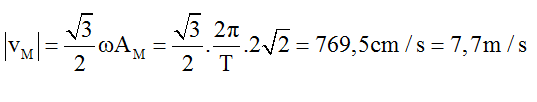
Câu 5: Sóng dừng hình thành trên một sợi dây đàn hồi OB, với đầu phản xạ B cố định và tốc độ lan truyền v = 400cm/s. Hình ảnh sóng dừng như hình vẽ. Sóng tới tại B có biên độ a = 2cm, thời điểm ban đầu hình ảnh sợi dây là đường (1), sau đó các khoảng thời gian là 0,005 s và 0,015 s thì hình ảnh sợi dây lần lượt là (2) và (3). Biết xM là vị trí phần tử M của sợi dây lúc sợi dây duỗi thẳng. Khoảng cách xa nhất giữa M tới phần tử sợi dây có cùng biên độ với M là
A. 28,56 cm B. 24 cm C. 24,66 cm D. 28 cm
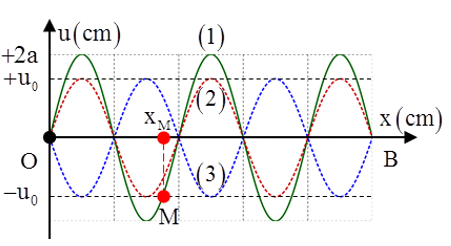
Lời giải:
Chọn C
Tương tự câu 5 ta tìm được chu kì của sóng T/8 = 0,005 => T = 0,04s và uo = √2a
Suy ra bước sóng λ = v.T = 16cm
M dao động đồng pha với bụng gần nhất nên tại thời điểm t1 (đường 1), phần tử bụng ở biên dương thì M cũng ở biên dương, do đó AM = uo = a√2 cm.
Suy ra M cách nút gần nhất một khoảng λ/8 = 2 cm
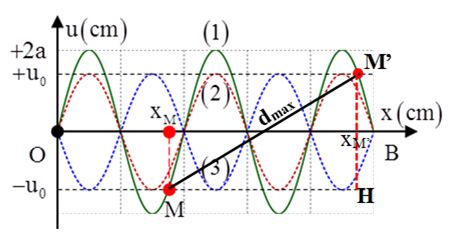
Điểm có cùng biên độ với M, xa M nhất là điểm M’ nằm ở bó sóng cuối cùng, luôn dao động ngược pha với M.
Từ hình vẽ ta có:
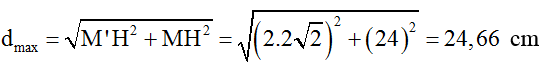
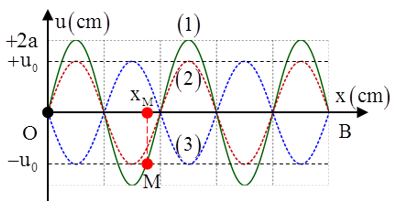
Câu 6: Sóng dừng ổn định trên sợi dây có chiều dài L = OB = 1,2m với hai đầu O và B là hai nút sóng. Tại thời điểm t = 0, các điểm trên sợi dây có li độ cực đại và hình dạng sóng là đường (1), sau đó một khoảng thời gian ∆t và 5∆t các điểm trên sợi dây chưa đổi chiều chuyển động và hình dạng sóng tương ứng là đường (2) và (3). Tốc độ truyền sóng trên dây bằng 6 m/s, biên độ của bụng sóng 4cm. Tốc độ cực đại của điểm M là
A. 140,81 cm/s B. 272,07 cm/s C. 247,12 cm/s D. 166,64 cm/s
Lời giải:
Chọn B
+ Bước sóng của sóng: 2,5λ = OB → λ = 0,48m
Chu kì của sóng: T = λ/v = 0,48/6 = 0,08s
+ Hai thời điểm (2) và (3) vị trí của các phần từ dây đối xứng với nhau qua vị trí cân bằng.
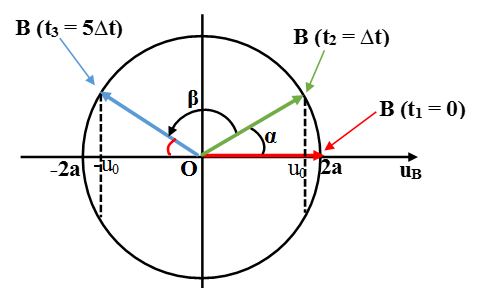
Sử dụng vòng tròn lượng giác ta có: β = ω.(t3 – t2) = ω.4∆t; α = ω.∆t → β = 4α
Mà β = 2(π/2 – α) = π - 2α → α = π/6.
Suy ra
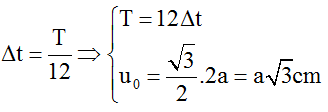
M dao động đồng pha với bụng gần nhất nên tại thời điểm t = 0 (đường 1), phần tử bụng ở biên âm thì M cũng ở biên âm, do đó AM = uo = a√3 = 2√3 cm
Tốc độ cực đại của M: