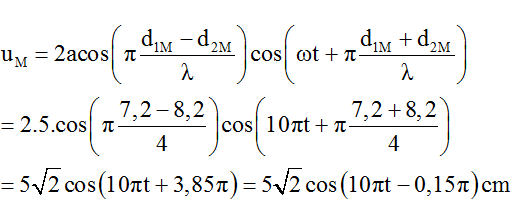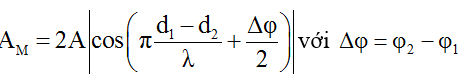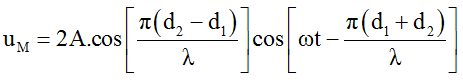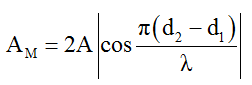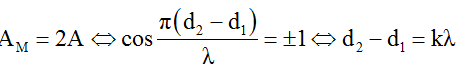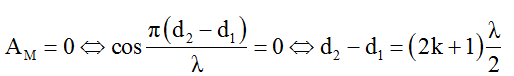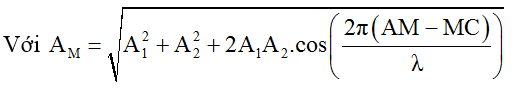Cách xác định, cách tìm biên độ, li độ, vận tốc, gia tốc trong giao thoa sóng hay, chi tiết - Vật Lí lớp 12
Cách xác định, cách tìm biên độ, li độ, vận tốc, gia tốc trong giao thoa sóng hay, chi tiết
Với Cách xác định, cách tìm biên độ, li độ, vận tốc, gia tốc trong giao thoa sóng hay, chi tiết Vật Lí lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập xác định, cách tìm biên độ, li độ, vận tốc, gia tốc trong giao thoa sóng từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

A. Phương pháp giải
1. Lý thuyết giao thoa tìm biên độ:
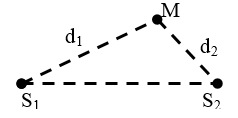
Phương trình sóng tại 2 nguồn: (Điểm M cách hai nguồn lần lượt d1, d2)
u1 = A1cos(2πft + φ1)
u2 = A2cos(2πft + φ2)
Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:
u1M = A1cos(2πft - 2πd1/λ+ φ1)
và u2M = A2cos(2πft - 2πd2/λ+ φ2)
* Nếu 2 nguồn cùng pha thì:
u1M = 2A2cos(2πft - 2πd1/λ)
u2M = A2cos(2πft - 2πd2/λ)
Phương trình giao tổng hợp sóng tại M: uM = u1M + u2M
Thế các số liệu từ đề cho để tính kết quả (giống như tổng hợp các dao động bằng phương pháp số phức).
B. Ví dụ minh họa
Ví dụ 1: Trên mặt thoáng của chất lỏng có 2 nguồn kết hợp A,B có phương trình dao động là: uA = uB = 4cos10πt (cm). Vận tốc truyền sóng là 3m/s.
a) Viết phương trình sóng tại M cách A, B một khoảng lần lượt là d1 = 15cm, d2 = 20cm.
b) Tìm biên độ và và pha ban đầu của sóng tại N cách A 45cm, cách B 60cm.
c) Tìm biên độ sóng tại O là trung điểm giữa 2 nguồn.
Hướng dẫn giải:
a) Bước sóng: λ = v/f = 300/5 = 60cm.
Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:
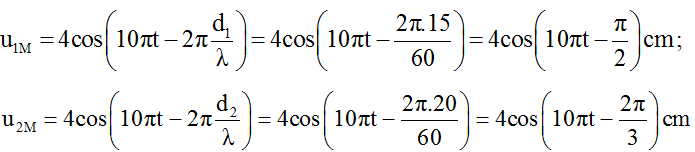
Sử dụng số phức ta xác định được phương trình giao tổng hợp sóng tại M:
uM = u1M + u2M = 4 cos(-π/12) cos(10πt - 7π/12) cm
b) Tương tự ta xác định được phương trình sóng tại N:
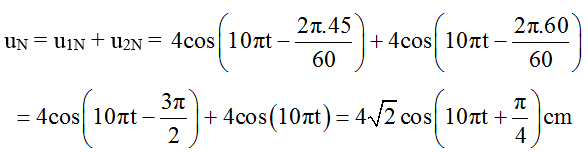
Vậy N dao động sóng với biên độ AN = 4√2 cm, pha ban đầu π/4 rad.
c) O là trung điểm giữa 2 nguồn (d1 = d2 = d), phương trình sóng tại O là:
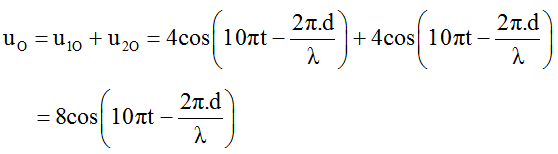
Biên độ sóng tại O là trung điểm giữa 2 nguồn là Ao = 8cm.
2. Nếu 2 nguồn cùng biên độ thì:
Phương trình sóng tại 2 nguồn: (Điểm M cách hai nguồn lần lượt d1, d2)
u1 = Acos(2πft + φ1)
u2 = Acos(2πft + φ2)
Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:
u1M = A1cos(2πft - 2πd1/λ+ φ1)
và u2M = A2cos(2πft - 2πd2/λ+ φ2)
Phương trình giao thoa sóng tại M: uM = u1M + u2M
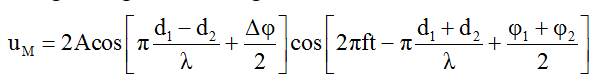
Biên độ dao động tại M:
a) Hai nguồn A, B dao động cùng pha
Từ phương trình giao thoa sóng:
Ta nhận thấy biên độ dao động tổng hợp là:
Biên độ đạt giá trị cực đại
Biên độ đạt giá trị cực tiểu
Chú ý: Nếu O là trung điểm của đoạn AB thì tại 0 hoặc các điểm nằm trên đường trung trực của đoạn A, B sẽ dao động với biên độ cực đại và bằng: AM = 2A (vì lúc này d1 = d2)
Từ phương trình sóng tại một điểm ta tìm được phương trình vận tốc, gia tốc cho điểm đó tương tự như cách làm trong dao động điều hòa.
Ví dụ 2: Hai nguồn sóng kết hợp trên mặt thoáng chất lỏng dao động theo phương trình uA = uB = 4cos10πt mm. Coi biên độ sóng không đổi, tốc độ truyền sóng v = 15cm/s. Hai điểm M, N cùng nằm trên một elip nhận A, B làm tiêu điểm có AM – BM = 1cm; AN – BN = 3,5cm. Tại thời điểm li độ của M là 3mm thì li độ của N tại thời điểm đó là
A. 3mm B. – 3mm C. - √3 mm D. - 3√3mm
Hướng dẫn giải:
Chọn D.
Bước sóng: λ = v/f = 15/5 = 3cm.
Phương trình giao thoa sóng:
Tại M:
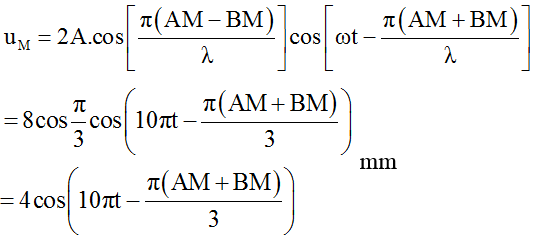
Tại N:
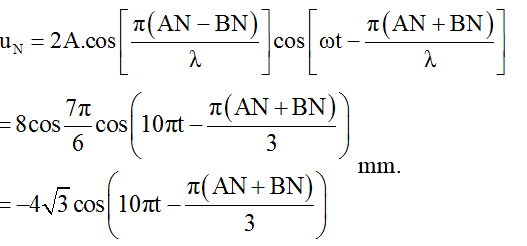
Vì hai điểm M, N cùng nằm trên một elip nhận A, B làm tiêu điểm nên:
AN + BN = AM + BM
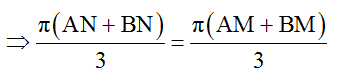
Do đó M và N dao động ngược pha nhau
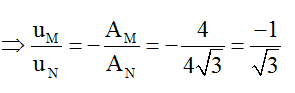
Thời điểm t, uM = 3mm → uN = -3√3 mm
Ví dụ 3: Trên mặt chất lỏng có hai nguồn S1 và S2 có phương trình lần lượt là u1 = u2 = 4cos(40πt) mm, tốc độ truyền sóng là 120 cm/s. Gọi I là trung điểm của S1S2. Hai điểm A, B nằm trên S1S2 lần lượt cách I một khoảng 0,5 cm và 2 cm. Tại thời điểm t gia tốc của điểm A là 12 cm/s2 thì gia tốc dao động tại điểm B có giá trị?
A. 4√3 cm/s2 B. 12√3 cm/s2 C. -4√3 cm/s2 D. -12cm/s2
Hướng dẫn giải:
Chọn C.
Bước sóng của sóng: λ = v/f = 120/20 = 6cm
Ý tưởng: ta có thể xem hiện tượng giao thoa sóng trên đoạn thẳng nối hai nguồn tương tự như hiện tượng sóng dừng trên dây. Hai nguồn này cùng pha nên khi xảy ra giao thoa thì I sẽ là một cực đại giao thoa, đóng vai trò là một bụng.
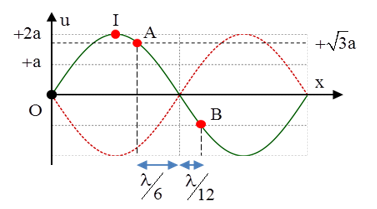
Từ hình vẽ ta thấy A và B nằm trên hai “bó sóng” khác nhau nên gia tốc phải ngược dấu
Ta có: 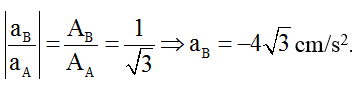
b) Hai nguồn A, B dao động ngược pha
Ta nhận thấy biên độ dao động tổng hợp là:
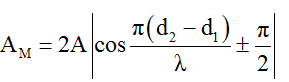
Chú ý: Nếu O là trung điểm của đoạn AB thì tại 0 hoặc các điểm nằm trên đường trung trực của đoạn A, B sẽ dao động với biên độ cực tiểu và bằng: AM = 0 (vì lúc này d1 = d2)
Ví dụ 4: Trên mặt nước tại hai điểm S1, S2 người ta đặt hai nguồn sóng kết hợp dao động điều hòa theo phương thẳng đứng với phương trình u1 = 8cos(40πt + π) và 8cos(40πt) (u1, u2 tính bằng mm). Biết tốc độ truyền sóng trên mặt nước là 144cm/s, coi biên độ sóng không đổi khi truyền sóng. Trên đoạn thẳng S1S2 điểm dao động với biên độ 8mm và cách trung điểm I của S1S2 một đoạn gần nhất là:
A. 0,25cm. B. 0,3cm. C. 0,75cm. D. 0,6cm.
Hướng dẫn giải:
Chọn D.
Bước sóng: λ = v/f = 7,2cm
Xét điểm M trên đoạn thẳng S1S2 có MS1 = d1, MS2 = d2, bằng hình học ta dễ dàng chứng minh được d1 – d2 = 2MI (giả sử d1 > d2)
Độ lệch pha hai sóng kết hợp tại M:
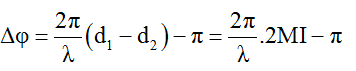
Biên độ sóng tại M:
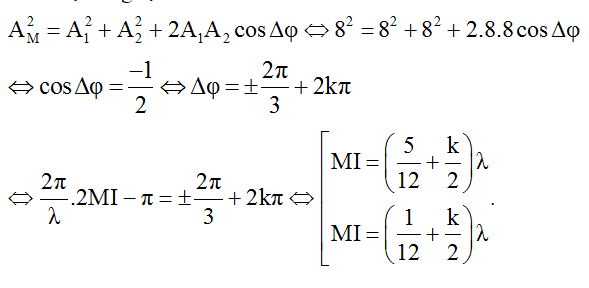
c) Hai nguồn A, B dao động vuông pha
Ta nhận thấy biên độ dao động tổng hợp là:
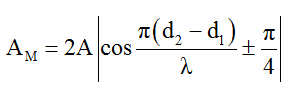
Chú ý: Nếu O là trung điểm của đoạn AB thì tại 0 hoặc các điểm nằm trên đường trung trực của đoạn A, B sẽ dao động với biên độ: AM = A√2 (vì lúc này d1 = d2).
Suy ra MImin = λ/12 = 0,6cm
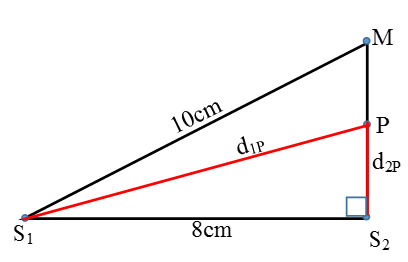
Ví dụ 5: Có hai nguồn dao động kết hợp S1, S2 trên mặt nước cách nhau 8cm, có phương trình dao động lần lượt là: uS1 = 2cos(10πt - π/4) mm ; uS2 = 2cos(10πt + π/4) mm Tốc độ truyền sóng trên mặt nước là 10cm/s. Xem biên độ của sóng không đổi trong quá trình truyền đi. Điểm M trên mặt nước cách S1 một khoảng là S1M = 10cm cách S2 khoảng S2M = 6cm Điểm dao động cực đại trên S2M cách S2 một đoạn lớn nhất bằng:
A. 3,07 cm. B. 2,33 cm. C. 3,57 cm. D. 6 cm.
Hướng dẫn giải:
Chọn A.
Bước sóng: λ = v/f = 2cm.
Ta thấy S1M2 = S2M2 + S1S22 nên MS2 vuông góc với S1S2.
Độ lệch pha dao động của hai sóng từ hai nguồn truyền đến tại điểm P trên đoạn S2M:
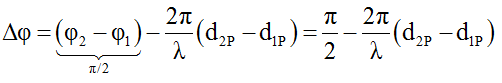
P dao động cực đại khi ∆φ = 2kπ (k ϵ Z).
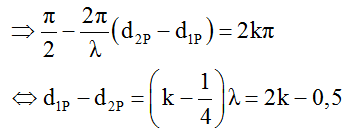
Mặt khác P thuộc đoạn S2M nên S1M – S2M ≤ d1P – d2P ≤ S1S2
↔ 10 – 6 ≤ 2k – 0,5 ≤ 8 ↔ 2,25 ≤ k ≤ 4,25
Vì k ϵ Z nên k = 3 hoặc k = 4
Ta có ∆PS1S2 vuông tại S2 nên:
d21P - d22P = S1S22 = 64
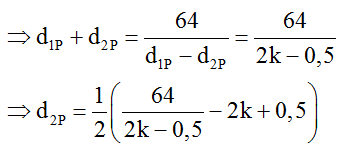
Để d2P = PS2 lớn nhất thì d1P – d2P nhỏ nhất ↔ k = 3. Khi đó: d2P(min) = 3,07 cm.
C. Bài tập vận dụng
Câu 1: Trên mặt nước cho hai nguồn sóng kết hợp S1, S2 có phương trình u1 = u2 = acosωt (cm), bước sóng 9cm. Coi biên độ sóng không đổi trong quá trình truyền. Trên mặt nước, xét elip nhận S1 và S2 là hai tiêu điểm, có hai điểm M và N sao cho: tại M hiệu đường đi của hai sóng từ hai nguồn S1 và S2 đến M là ∆dM = d1M – d2M = 2,25cm, tại N ta có ∆dN = d1N – d2N = 6,75cm. Tại thời điểm t thì vận tốc dao động của M là cm/s, khi đó vận tốc dao động tại N là
A. 40√3 cm/s B. -20√3 cm/s C. -40√3 cm/s D. 20√3 cm/s
Lời giải:
Chọn D.
Phương trình dao động của các điểm M và N được xác định bởi
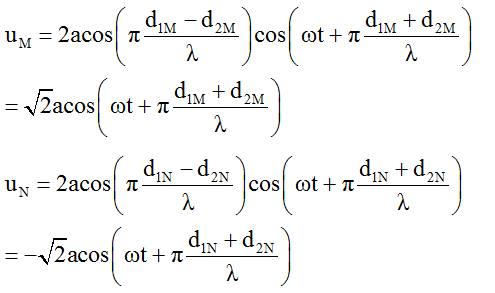
Các điểm nằm trên cùng elip nên d1M + d2M = d1N + d2N, suy ra M dao động ngược pha với N cm/s.
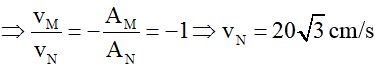
Câu 2: Trên mặt nước có hai nguồn kết hợp cùng pha cùng biên độ A. Tại điểm M trong vùng giao thoa, điểm M có biên độ 2A. Nếu tăng tần số của hai nguồn lên hai lần thì biên độ lúc này là:
A. 0. B. A C. A√2 D. 2A
Lời giải:
Chọn D.
Điểm M là cực đại nên d1 – d2 = kλ
Khi f’ = 2f thì λ’ = λ/2.
Ta thấy d1 – d2 = kλ = k.(2λ’) = 2k.λ’ nên d1 – d2 = k’.λ’ (với k’ = 2k ϵ Z).
Suy ra M vẫn là cực đại. A’M = 2A.
Câu 3: Trên mặt một chất lỏng có hai nguồn sóng kết hợp cùng pha có biên độ a và 2a dao động vuông góc với mặt thoáng chất lỏng. Nếu cho rằng sóng truyền đi với biên độ không thay đổi thì tại một điểm cách hai nguồn những khoảng d1 = 12,75λ và d2 = 7,25λ sẽ có biên độ dao động a0 là bao nhiêu?
A. ao = a. B. a < ao < 3a C. ao = 2a. D. ao = 3a.
Lời giải:
Chọn A.
Độ lệch pha của 2 sóng từ hai nguồn gây ra tại M là:
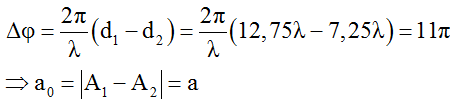
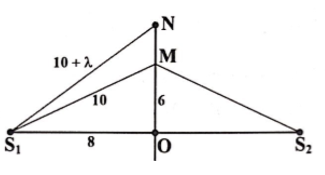
Câu 4: Trong thí nghiệm giao thoa sóng nước, hai nguồn S1, S2 cách nhau 16cm, dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 80Hz. Tốc độ truyền sóng trên mặt nước là 40cm/s. Ở mặt nước, gọi d là trung trực của S1S2. Trên d, điểm M cách S1 là 10cm, điểm N dao động cùng pha với M và gần M nhất sẽ cách M một đoạn bằng bao nhiêu?
A. 0,80cm. B. 0,88cm. C. 1,25cm. D. 2,25cm
Lời giải:
Chọn A.
Bước sóng: λ = v/f = 0,5 cm
Các điểm trên trung trực d của S1S2 thỏa mãn d1 = d2 = d, nên có phương trình dao động là:
u = 2Acos[ωt + φ - 2πd/λ] (φ là pha ban đầu của hai nguồn).
Độ lệch pha của dao động tại M và N là: ∆φMN = φM - φN = (2π(dN - dM))/λ
Điều kiện để N đồng pha với M là: ∆φMN = 2kπ (k ϵ Z)
→ dN – dM = kλ.
Vì MS1 = dM = 10cm = 20λ → NS1 = dN = 21λ hoặc 19λ.
* Nếu dN = 21λ = 10,5cm thì
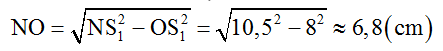
→ MN = ON – OM = 0,8cm.
* Nếu dN = 19λ = 9,5cm thì
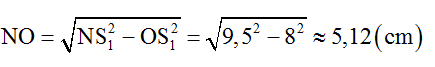
→ MN = ON – OM = 0,88cm.
Vậy NMmin = 0,8cm.
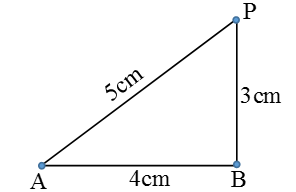
Câu 5: Trên bề mặt chất lỏng có hai nguồn kết hợp A, B cách nhau 4cm, dao động cùng pha, cùng tần số, cùng phương thẳng đứng và cùng biên độ a. Biết bước sóng là 2cm. Xét điểm P nằm trên mặt chất lỏng và nằm trên đường vuông góc với AB tại B, cách B một đoạn 3cm. Biên độ dao động tổng hợp tại P là:
A. 2a B. a C. 0 D. 3a
Lời giải:
Chọn A.
Điểm P có: d1 = PA = √(PB2+ AB2) ; d2 = PB = 3cm.
Độ lệch pha của hai sóng kết hợp tại P:
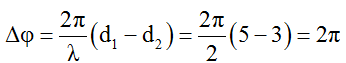
Hai sóng kết hợp sẽ tăng cường lẫn nhau nên P cực đại.
Biên độ tổng hợp tại P: AP = a + a = 2a
Câu 6: Trên mặt chất lỏng có hai nguồn dao động A, B có phương trình lần lượt là u1 = u2 = 5√3 cos (40πt) (cm) tốc độ truyền sóng là 60 cm/s. Hai điểm P và Q trên AB cách trung điểm I của AB lần lượt là 0,25 cm và 1 cm. Tại thời điểm t, li độ của P là -12cm và đang giảm thì vận tốc dao động tại Q là:
A. 120π√3 cm/s B. -120π√3 cm/s
C. -48π√2 cm/s D. 48π√2 cm/s
Lời giải:
Chọn A.
Phương trình sóng tại P và Q là:
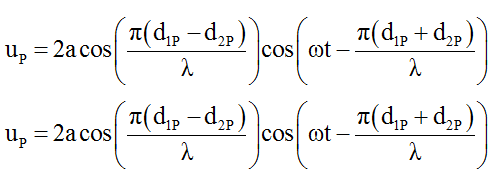
Vì hai điểm P và Q trên AB nên ta dễ dàng chứng minh được:
d1P – d2P = 2.PI = 0,5cm và d1Q – d2Q = 2.QI = 2cm; d1P + d2P = d1Q + d2Q = AB
Suy ra:
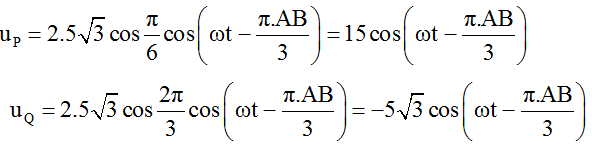
Tại thời điểm t, li độ của P là -12cm và đang giảm nên vận tốc của P là:
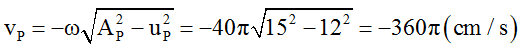
P và Q dao động ngược pha nhau nên ta có:
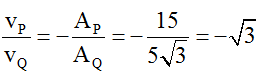
Suy ra vận tốc dao động tại điểm Q tại thời điểm t là: vQ = 120π√3 cm/s
Câu 7: Tại mặt thoáng của một chất lỏng có bốn điểm thẳng hàng được sắp xếp theo thứ thự A, B, C, D với AB = 35cm, BC = 10,5cm, CD = 19,5cm. Điểm M thuộc mặt chất lỏng cách A và C tương ứng là AM = 27,3cm, MC = 36,4cm. Hai nguồn sóng dao động theo phương vuông góc với mặt nước với phương trình u1 = 3cos100πt cm và u1 = 4cos100πt cm Biết vận tốc truyền sóng trên mặt chất lỏng bằng 12,3 m/s. Coi biên độ sóng các nguồn truyền đến M bằng biên độ sóng của mỗi nguồn. Khi hai nguồn sóng đặt ở A và C thì các phần tử chất lỏng tại M dao động với biên độ A1, khi hai nguồn sóng đặt tại B và D thì các phần tử chất lỏng tại M dao động với biên độ A2. Giá trị A1 và A2 tương ứng là
A. 2,93 cm và 6,93 cm B. 5,1 cm và 1,41 cm
C. 5 cm và 2,93 cm D. 2,93 cm và 7 cm
Lời giải:
Chọn D.
Bước sóng: λ = v/f = 12,3/50 = 0,246m = 24,6cm.
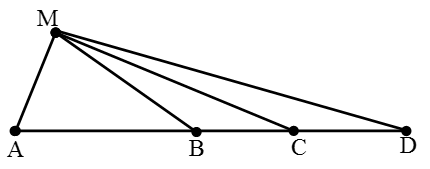
Dễ thấy rằng tam giác AMC vuông tại M, từ đó ta tìm được độ dài của các đoạn thẳng:
MB = 28,7cm; MD = 53,3cm
Phương trình sóng do hai nguồn tại A và B truyền đến M
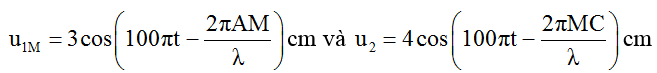
Dao động tổng hợp tại M khi đó có dạng uM = AMcos(100πt + φ).
Với
Áp dụng cho hai trường hợp ta thu được A1 = 2,93cm và A2 = 7cm.
Câu 8: Trên mặt nước có hai nguồn phát sóng kết hợp A, B có cùng biên độ a = 2 cm, cùng tần số f = 20 Hz, ngược pha nhau. Coi biên độ sóng không đổi, vận tốc sóng v = 80 cm/s. Biên độ dao động tổng hợp tại điểm M có AM = 12 cm, BM = 10 cm là:
A. 4 cm B. 2 cm. C. 2√2 cm. D. 0 cm.
Lời giải:
Chọn A.
Ta có λ = v/f = 4cm , AM – BM = 2cm = (k + 0,5)λ (với k = 0)
Vì hai nguồn ngược pha nên điểm M dao động cực đại
=> Biên độ dao động tổng hợp tại M: AM = 2a = 4cm.
Câu 9: Ở bề mặt một chất lỏng có hai nguồn phát sóng kết hợp S1 và S2 cách nhau 20cm. Hai nguồn này dao động theo phương thẳng đứng có phương trình lần lượt là u1 = 5cos40πt (mm) và u2 = 5cos(40πt + π) (mm). Tốc độ truyền sóng trên mặt chất lỏng là 80 cm/s. Xét các điểm trên S1S2. Gọi I là trung điểm của S1S2; M nằm cách I một đoạn 3cm sẽ dao động với biên độ:
A. 0 mm B. 5 mm C. 10 mm D. 2,5 mm
Lời giải:
Chọn C.
Bước sóng: λ = v/f = 80/20 = 4cm.
Biên độ dao động tổng hợp tại điểm M là:
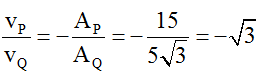
Vì M cách trung điểm I một đoạn 3cm nên
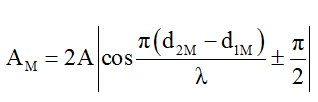
Câu 10: Hai nguồn phát sóng kết hợp A, B với AB = 16cm trên mặt thoáng chất lỏng, dao động phương trình uA = 5cos30πt(mm), uB = 5cos(30πt + π/2) (mm). Coi biên độ sóng không đổi, tốc độ truyền sóng v = 60cm/s. Gọi O là trung điểm của AB, điểm đứng yên trên đoạn AB gần O nhất và xa O nhất cách một đoạn tương ứng là:
A. 1cm và 8cm. B. 0,25cm và 7,75cm. C. 1cm và 6,5cm. D. 0,5cm và 7,5cm.
Lời giải:
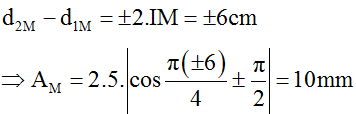
Chọn D
Xét điểm M có tọa độ x như hình vẽ.
Ta có:
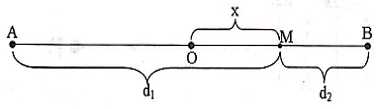
Độ lệch pha hai sóng kết hợp tại M thuộc đoạn AB là:
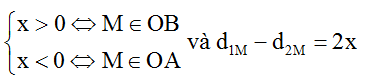
Nếu M là cực tiểu thì ∆φ = (2k + 1)π, hay x = 2k + 0,5 (cm).
Điều kiện -0,5AB ≤ x ≤ 0,5AB suy ra -4,25 ≤ k ≤ 1,75
Vì k ϵ Z nên ta có bảng giá trị của k.
| k | -4 | -3 | -2 | -1 | 0 | 1 |
| x (cm) | -7,5 | -5,5 | -3,5 | -1,5 | 0,5 | 2,5 |
| OM | 7,5 | 5,5 | 3,5 | 1,5 | 0,5 | 2,5 |
Vậy OMmin = 0,5cm; OMmax = 7,5cm.
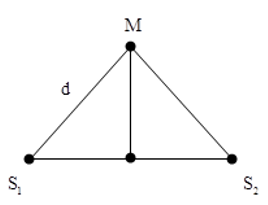
Câu 11: Hai nguồn sóng kết hợp trên mặt nước S1 và S2 dao động với phương trình u1 = a.sinωt và u2 = a.cosωt. Biết O là trung điểm của S1S2 và S1S2 = 9λ. Điểm M trên trung trực của S1S2 gần O nhất dao động cùng pha với S1 cách S1 một khoảng bao nhiêu?

Lời giải:
Chọn C
Sóng do hai nguồn gởi đến điểm M trên trung trực của S1S2
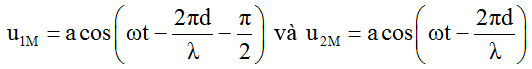
Phương trình dao động tổng hợp tại M:
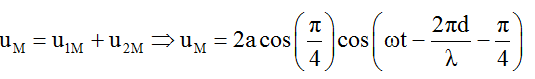
Để M cùng pha với S1 thì
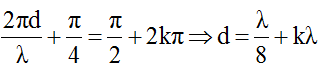
Ta lấy giá trị nhỏ nhất của k thỏa mãn bất phương trình:
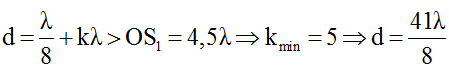
Câu 12: Trong thí nghiệm giao thoa sóng người ta tạo ra trên mặt nước 2 nguồn sóng A, B dao động với phương trình uA = uB = 5cos10πt (cm). Vận tốc sóng là 20 cm/s. Coi biên độ sóng không đổi. Viết phương trình dao động tại điểm M cách A, B lần lượt 7,2 cm và 8,2 cm.
A. uM = √2 cos(10πt + 0,15 π) cm. B. uM = √2 cos(10πt - 0,15 π) cm.
C. uM = 5√2 cos(10πt + 0,15 π) cm D. uM = 5√2 cos(10πt - 0,15 π) cm.
Lời giải:
Chọn C
Bước sóng: λ = v/f = 20/5 = 4cm.
Phương trình dao động của điểm M được xác định bởi: