Cách giải các dạng bài tập về Sóng âm hay, chi tiết - Vật Lí lớp 12

Cách giải các dạng bài tập về Sóng âm hay, chi tiết

Tài liệu Cách giải các dạng bài tập về Sóng âm hay, chi tiết Vật Lí lớp 12 sẽ tóm tắt kiến thức trọng tâm về Sóng âm từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Vật Lí lớp 12.

A. Phương pháp

Sóng âm là là sóng dọc cơ học lan truyền trong các môi trường rắn, lỏng, khí, (không lan truyền trong chân không).

- Tai con người chỉ có thể cảm nhận được (nghe được) các âm có tần số từ 16 Hz đến 20000Hz. Các sóng âm có tần số nhỏ hơn 16 Hz được gọi là hạ âm. Các sóng âm có tần số lớn hơn 20000 Hz được gọi là siêu âm.

- Tốc độ truyền âm giảm trong các môi trường theo thứ tự : rắn, lỏng, khí. Tốc độ truyền âm phụ thuộc vào tính chất môi trường, nhiệt độ của môi trường và khối lượng riêng của môi trường. Khi nhiệt độ tăng thì tốc độ truyền âm cũng tăng.

1.Các đặc trưng vật lý của âm

- Tần số âm: Âm trầm có tần số nhỏ, âm cao có tần số lớn.

- Cường độ âm I tại một điểm là đại lượng đo bằng lượng năng lượng mà sóng âm tải qua một đơn vị diện tích đặt tại điểm đó, vuông góc với phương truyền âm trong một đơn vị thời gian.

Nếu có n nguồn âm giống nhau, kích thước nhỏ phát ra sóng âm đồng đều theo mọi hướng:

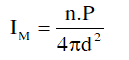
Trong đó:

I là cường độ âm tại M (W/m²).

P là công suất của nguồn âm (W).

d là khoảng cách tính từ nguồn đến điểm M (m).

Mức cường độ âm L tại M:

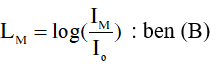
Io = 10 ^{- 12} W/m².

1 B = 10 dB.

- Đồ thị dao động âm và phổ của âm

Âm thanh phát ra trong không khí được thu lại và chuyển thành dao động của các cần rung hoặc dao động điện có cùng tần số.

2.Các đặc trưng sinh lý của âm:

Âm có 3 đặc trưng sinh lý là : độ cao, độ to và âm sắc. Các đặc trưng của âm nói chung phụ thuộc vào cảm thụ âm của tai con người.

- Độ cao

    + Đặc trưng cho tính trầm hay bổng của âm.

    + Phụ thuộc vào tần số âm. Âm có tần số lớn gọi là âm bổng và âm có tần số nhỏ gọi là âm trầm.

- Độ to Là đại lượng đặc trưng cho tính to hay nhỏ của âm, phụ thuộc vào tần số âm và mức cường độ âm.

- Âm sắc có liên quan mật thiết với đồ thị dao động âm ( tần số và biên độ) hoặc phổ của âm. Hai nhạc cụ khác nhau phát ra cùng một nốt nhạc, cùng độ cao ( cùng tần số), cùng cường độ sẽ chắc chắn khác nhau về âm sắc.

Ngưỡng nghe : là giá trị nhỏ nhất của mức cường độ âm mà tai con người có thể nghe được, I = I_o = 10^-12W/m² ⇔ L = 0 dB

Ngưỡng đau : Là cường độ âm lớn tới mức tạo cảm giác đau trong tai, I_max = 10 W/m² ⇔ L = 130 dB

Miền nghe được : là giá trị của mức cường độ âm trong khoảng giữa ngưỡng nghe và ngưỡng đau ( 0 dB – 130 dB).

3. Nhạc âm và tạp âm:

Nhạc âm là những âm có tần số xác định và đồ thị dao động là đường cong hình sin. Tạp âm là những âm có tần số không xác định và đồ thị dao động là những đường cong phức tạp.

4. Âm cơ bản và họa âm:

Âm cơ bản có tần số f1 (tần số nhỏ nhất mà nhạc cụ có thể phát ra, có biên độ âm lớn nhất)

Các họa âm có tần số bằng bội số tương ứng với âm cơ bản.

    + Dây đàn (2 đầu cố định): các họa âm bằng nguyên lần âm cơ bản: f₂ = 2f_o, f₃ = 3f_o,..., f_n = nf_o

    + Ống sáo (1 đầu nót, 1 đầu hở): các họa âm bằng nguyên lẻ lần âm cơ bản: f₁ = f_o, f₂ = 3f_o, f₃ = 5f_o, f₄ = 7f_o, ...

B. Ví dụ

Ví dụ 1: Hai họa âm liên tiếp do một dây đàn phát ra có tần số hơn kém nhau 56 Hz, họa âm thứ ba và họa âm thứ năm có tần số bằng bao nhiêu?

Hướng dẫn:

Hai họa âm liên tiếp hơn kém nhau 56 Hz nên ta có:

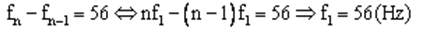
Từ đó ta có tần số của họa âm thứ ba và thứ năm là:

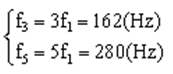
Ví dụ 2: Một dây đàn phát ra âm cơ bản có tần số f₁ = 420 Hz. Một người chỉ nghe được âm cao nhất có tần số là 18000 Hz, tìm tần số lớn nhất mà nhạc cụ này có thể phát ra để người đó nghe được.

Hướng dẫn:

Gọi f_n là âm mà người đó nghe được, ta có: f_n = n. f¹ = 420n

Theo bài

f_n < 18000 ⇔ 420n < 18000 ⇒ n < 42,8 (1)

Từ đó giá trị lớn nhất của âm mà người đó nghe được ứng với giá trị nguyên lớn nhất thỏa mãn (1) là n = 42

Vậy tần số âm lớn nhất mà người đó nghe được là 420.42 = 17640 (Hz).

Ví dụ 3: Mức cường độ âm tại một điểm cách một nguồn phát âm 1 m có giá trị là 50 dB. Một người xuất phát từ nguồn âm, đi ra xa nguồn âm thêm 100 m thì không còn nghe được âm do nguồn đó phát ra. Lấy cường độ âm chuẩn là I_o = 10^-12(W/m²) , sóng âm phát ra là sóng cầu thì ngưỡng nghe của tai người này là bao nhiêu?

Hướng dẫn:

Cường độ âm được tính bởi I = P/S

Do âm phát ra dạng sóng cầu nên:

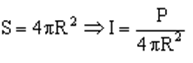
Do đó

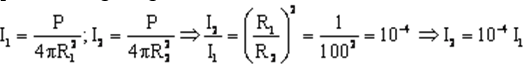
Mức cường độ âm gây ra tại điểm cách nguồn âm 100 m là:

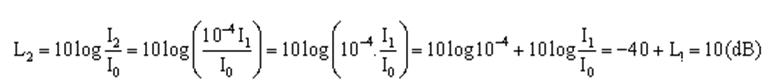
Vậy ngưỡng nghe của tai người này là 10 (dB).

Ví dụ 4: Hai âm có mức cường độ âm chênh lệch nhau 20 dB. Tỉ số của cường độ âm của chúng là bao nhiêu?

Hướng dẫn:

Áp dụng công thức tính mức cường độ âm ta có:

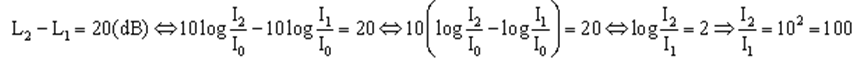
Vậy tỉ số cường độ âm của hai âm đó là 100 lần.

Ví dụ 5: Một người đứng cách nguồn âm một khoảng d thì cường độ âm là I. Khi người đó tiến ra xa nguồn âm một đoạn 40m thì cường độ âm giảm chỉ còn I/9 . Tính khoảng cách d.

Hướng dẫn:

Ta có:

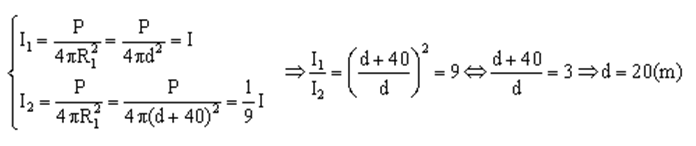
Ví dụ 6: Mức cường độ của một âm là L = 30(dB) . Hãy tính cường độ của âm này theo đơn vị W/m² . Biết cường độ âm chuẩn là I_o = 10^-12 W/m² . Cường độ âm tăng 100 lần thì mức cường độ âm tăng bao nhiêu dB?

Hướng dẫn:

Mức cường độ âm tính theo đơn vị (dB) là:

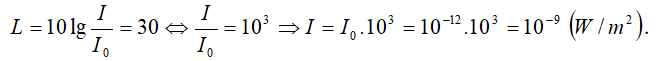
Mức cường độ âm tính theo đơn vị (dB) là:

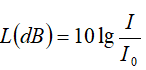
    + Khi cường độ tăng 100 lần tức là bằng 100 I thì

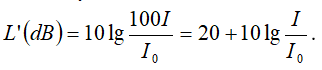
    + Vậy mức cường độ âm tăng thêm 20(dB).

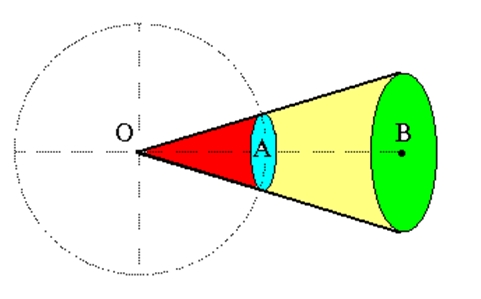
Ví dụ 7: Tại một điểm A nằm cách xa nguồn âm O (coi như nguồn điểm) một khoảng OA = 1(m) , mức cường độ âm là L_A = 90 (dB) . Cho biết ngưỡng nghe của âm chuẩn I_o = 10^-12 W/m² .

1) Tính cường độ I_o của âm đó tại A

2) Tính cường độ và mức cường độ của âm đó tại B nằm trên đường OA cách O một khoảng . Coi môi trường là hoàn toàn không hấp thụ âm.

3) Giả sử nguồn âm và môi trường đều đẳng hướng. Tính công suất phát âm của nguồn O.

Hướng dẫn:

1) Mức cường độ âm tại A tính theo đơn vị (dB) là:

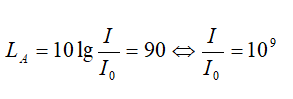
⇒ I = I_o. 10⁹ = 10_-12 . 10⁹ = 10^-3 (W/m²)

2) Công suất âm của nguồn O bằng công suất âm trên toàn diện tích mặt cầ u bán kính OA và bằng công suất âm trên toàn diện tích mặt cầu bán kính OB tức là: W_o = I_A. S_A = I_B. S_B (1) (xem hình vẽ).

Trong đó I_A, I_B là cường độ âm tại A và B; S_A, S_B là diện tích các mặt cầu tâm O bán kính OA và OB.

    + Từ đó rút ra:

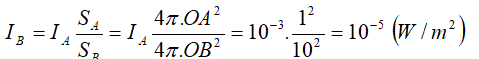
    + Mức cường độ của âm đó tại B là:

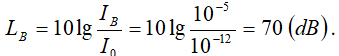
3) Công suất của nguồn âm tính theo (1), bằng năng lượng truyền qua diện tích mặt cầu tâm O bán kính OA trong 1 giây