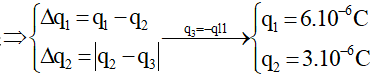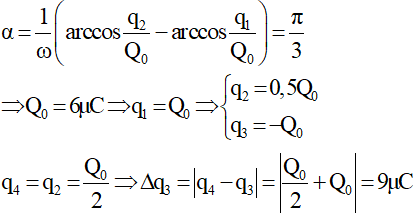Cách viết biểu thức điện áp, cường độ dòng điện, điện tích trong mạch dao động LC cực hay - Vật Lí lớp 12

Cách viết biểu thức điện áp, cường độ dòng điện, điện tích trong mạch dao động LC cực hay

Với Cách viết biểu thức điện áp, cường độ dòng điện, điện tích trong mạch dao động LC cực hay Vật Lí lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập viết biểu thức điện áp, cường độ dòng điện, điện tích trong mạch dao động LC từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

A. Phương pháp giải

I. Phương pháp chung.

a) Các biểu thức u, i, q.

* Biểu thức điện tích hai bản tụ điện: q = Q₀cos(ω + φ_q) C.

* Biểu thức cường độ dòng điện chạy trong cuộn dây:

i = q’ = I₀cos(ω + φ_q + π/2) (A) với I₀ = ωQ₀.

* Biểu thức hiệu điện thế hai đầu tụ điện: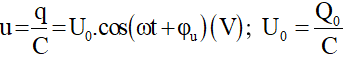

b) Các mối quan hệ về pha, biên độ và công thức độc lập.

* Quan hệ về pha của các đại lượng: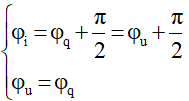

* Quan hệ về các biên độ:

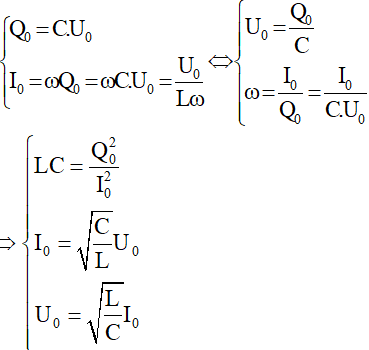
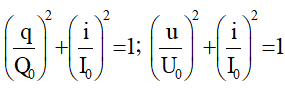
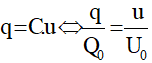
* Công thức độc lập: và

+ Hệ quả: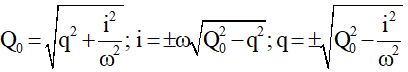

+ Đồ thị biểu diễn sự phụ thuộc các mối quan hệ:

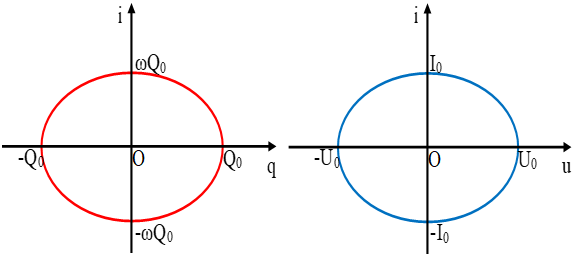
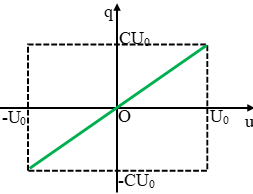
* Chú ý:

- Khi tụ phóng điện thì q và u giảm và ngược lại khi tụ nạp điện thì q và u tăng .

- Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn cực đại là Δt = T/2

- Khoảng thời gian ngắn nhất Δt để điện tích trên bản tụ này tích điện bằng một nửa giá trị cực đại là T/6.

- Liên hệ giữa giá trị biên độ và hiệu dụng: U₀ = U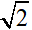 ; I₀ = I A.

B. Ví dụ minh họa

Ví dụ 1: Một cuộn dây thuần cảm, có độ tự cảm L = 2/π (H), mắc nối tiếp với một tụ điện có điện dung C = 3,18 (μF). Điện áp tức thời trên cuộn dây có biểu thức u_L = 100cos(ωt – π/6) V. Viết biểu thức của cường độ dòng điện trong mạch và điện tích giữa hai bản?

Hướng dẫn

Tần số góc dao động của mạch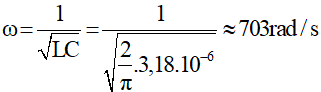

Điện áp giữa hai đầu cuộn dây cũng chính là điện áp giữa hai đầu tụ điện.

u_C = u_L = u = 100cos(ωt – π/6) V

Khi đó, Q₀ = CU₀ = 3,18.10^-6.100 = 3,18.10^-4 (C).

Do u và q cùng pha nên φ_q = φ_u = -π/6 rad → q = 3,18.10^-4 cos(700t - π/6)C.

Ta lại có 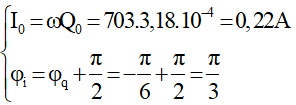→ i = 0,22cos(700t + π/3 ) A

Ví dụ 2: Cho mạch dao động lí tưởng với C = 1 nF, L = 1 mH, điện áp hiệu dụng của tụ điện là U_C = 4 V. Lúc t = 0, u_C = 2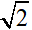 V và tụ điện đang được nạp điện. Viết biểu thức điện áp trên tụ điện và cường độ dòng điện chạy trong mạch dao động.

Hướng dẫn

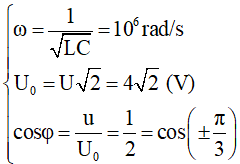
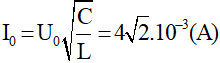
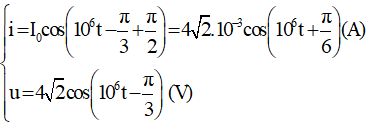
Ta có: ; vì tụ đang nạp điện nên φ=-π/3 rad.

Vì nên

Ví dụ 3: Một mạch dao động điện từ lí tưởng đang có dao động điện từ tự do. Tại thời điểm t = 0, tụ điện bắt đầu phóng điện. Sau khoảng thời gian ngắn nhất ∆t = 10^-6s thì điện tích trên một bản tụ điện bằng một nửa giá trị cực đại. Tính chu kì dao động riêng của mạch.

Hướng dẫn

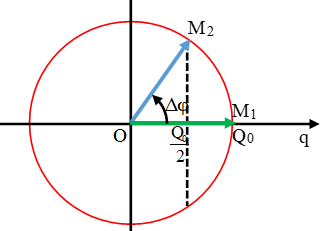
Ở thời điểm đầu (t = 0), điện tích trên một bản tụ là: q₁ = Q₀.

Sau khoảng thời gian ngắn nhất ∆t, điện tích trên một bản tụ điện là: q₂ = Q₀/2.

Ta có: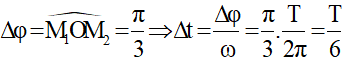

→ Chu kì dao động riêng của mạch là: T = 6∆t = 6.10^-6s.

Ví dụ 4:

Hai mạch dao động điện từ LC lí tưởng đang có dao động điện từ tự do cùng tần số với các cường độ dòng điện tức thời trong hai mạch là i₁ và i₂ được biểu diễn như hình vẽ. Tổng điện tích của hai tụ điện trong hai mạch ở cùng một thời điểm có giá trị lớn nhất bằng

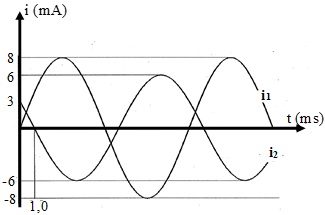
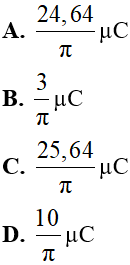
Hướng dẫn

Chọn A

Từ đồ thị ta được:

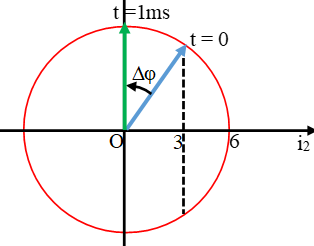
Phân tích đường biểu diễn i₂ và sử dụng vòng tròn lượng giác ta được:

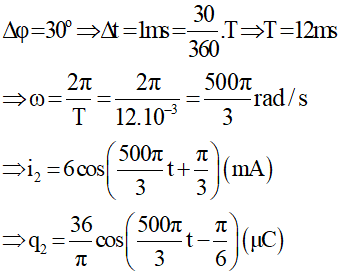
Tương tự ta tìm được biểu thức của i₁:

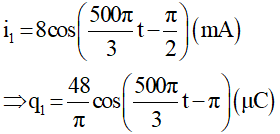
Sử dụng số phức dạng lượng giác, dùng máy tính Casio fx 570VN Plus ta được:

Tổng điện tích của hai tụ điện trong hai mạch ở cùng một thời điểm là:

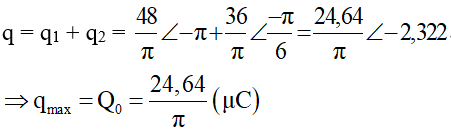
Ví dụ 5: Một mạch dao động LC lí tưởng gồm một cuộn cảm thuần L và tụ điện C có hai bản A và B. Trong mạch đang có dao động điện từ tự do với chu kì T, biên độ điện tích của tụ bằng Q₀. Tại thời điểm t, điện tích bản A là q_A = Q₀/2 đang tăng, sau khoảng thời gian ∆t nhỏ nhất thì điện tích của bản B là q_B = Q₀/2. Tỉ số ∆t/T bằng

A. 1/3.

B. 1/6.

C. 0,75.

D. 1/2.

Hướng dẫn

Chọn D.

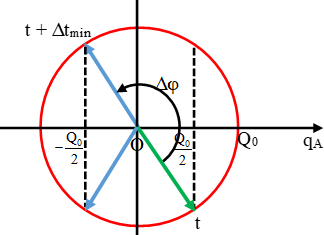
Hai bản A và B của cùng 1 tụ điện luôn có điện tích trái dấu nhau.

Do vậy ở thời điểm t + ∆t khi q_B = Q₀/2 thì q_A = - Q₀/2.

Sử dụng vòng tròn lượng giác biểu diễn q_A. Ta thấy ∆t_min ứng với góc quay ∆φ = π (rad)

→ ∆t_min = T/2 → ∆t/T = ½.

Ví dụ 6: Mạch dao động LC đang thực hiện dao động điện từ tự do với chu kỳ T. Tại thời điểm nào đó dòng điện trong mạch có cường độ 8π (mA) và đang tăng, sau đó khoảng thời gian 3T/4 thì điện tích trên bản tụ có độ lớn 2.10^-9 C. Chu kỳ dao động điện từ của mạch bằng

A. 0,5 ms

B. 0,25ms

C. 0,5μs

D. 0,25s

Hướng dẫn

Chọn C

Tại thời điểm t₁ bất kỳ, ta luôn có q₁ và i₁ vuông pha nhau → 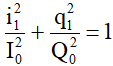(1)

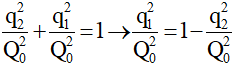
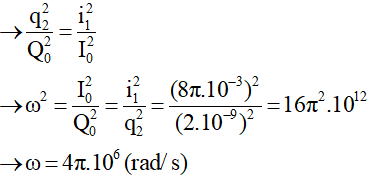
Tại thời điểm t₁ + 3T/4, q₁ và q₂ vuông pha nhau → (2)

→T = 2π/ω = 0,5.10^-6 (s) = 0,5μs.

Ví dụ 7 (ĐH 2013): Hai mạch dao động điện từ lý tưởng đang có dao động điện từ tự do. Điện tích của tụ điện trong mạch dao động thứ nhất và thứ hai lần lượt là q₁ và q₂ với 4q₁² + q₂²=1,3.10^-17, q tính bằng C. Ở thời điểm t, điện tích của tụ điện và cường độ dòng điện trong mạch dao động thứ nhất lần lượt là 10^-9C và 6mA, cường độ dòng điện trong mạch dao động thứ hai có độ lớn bằng:

A. 10mA

B. 6mA

C. 4mA

D. 8mA.

Hướng dẫn

Chọn D.

Từ biểu thức: 4q₁² + q₂²=1,3.10^-17(1)

Ta lấy đạo hàm hai vế theo thời gian, ta được: 2.4.q₁.i₁ + 2.q₂.i₂ = 0 (chú ý q₁, q₂ là hàm của thời gian)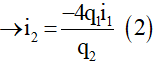

Theo lí thuyết, ta thay các giá trị q₁ = 10^-9C và i₁ = 6mA vào biểu thức (1) ta được:

│q₂│= 3.10^-9C.

Thế q₂ vào (2) ta được: │i₂│= 8mA.

C. Bài tập vận dụng

Câu 1: Một mạch dao động LC lí tưởng có C = 5 μF, L = 50 mH. Hiệu điện thế cực đại trên tụ là U₀ = 6V. Khi hiệu điện thế trên tụ là u = 4V thì độ lớn của cường độ của dòng trong mạch là:

A. i = 4,47 (A)

B. i = 2 (A)

C. i = 2 (mA)

D. i = 44,7 (mA)

Lời giải:

Hướng dẫn

Chọn D

Ta có u và i vuông pha nhau nên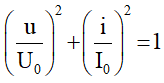

Mà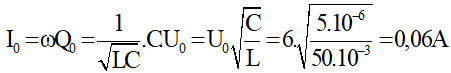

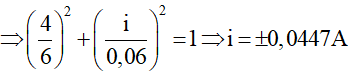
Câu 2: Cho mạch dao động LC. Biết điện tích trên tụ phụ thuộc thời gian theo biểu thức q = 3cos(10⁵t + π/2) μC. Tìm cường độ dòng điện cực đại chạy trong mạch

A. 3.10^-5 A

B. 3A

C. 3.10⁵A

D. 0,3A

Lời giải:

Hướng dẫn

Chọn D

Ta có: q = 3cos(10⁵t + π/2) μC → Q₀ = 3μC = 3.10^-6C; ω = 10⁵ rad/s.

Suy ra cường độ dòng điện cực đại chạy trong mạch: I₀ = Q₀.ω = 0,3A.

Câu 3: Một mạch dao động gồm cuộn dây có L = 0,2 H và tụ điện C = 10μF thực hiện dao động tự do. Biết cường độ cực đại trong khung là I₀ = 12.10^-3A. Khi cường độ dòng điện tức thời i = 0,01 A thì điện áp cực đại và điện áp tức thời giữa hai bản tụ lần lượt là:

A. 5,4 V; 2,94 V

B. 1,7 V; 0,94 V

C. 1,7 V; 20,0 V

D. 5,4 V; 0,90 V

Lời giải:

Hướng dẫn

Chọn B

Khi cường độ dòng điện tức thời i = 0,01A thì điện áp cực đại và điện áp tức thời giữa hai bản tụ lần lượt là:

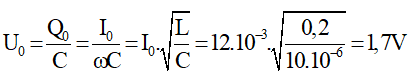
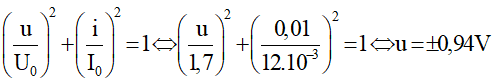
Câu 4: Một mạch dao động LC lí tưởng có L = 40mH, C = 25µF, điện tích cực đại của tụ q₀ = 10^-9C. Khi điện tích của tụ bằng 6.10^-10 C thì dòng điện trong mạch có độ lớn.

A. 8.10^-7A.

B. 6.10^-7A.

C. 3.10^-7A.

D. 5.10^-7A.

Lời giải:

Hướng dẫn

Chọn A.

Tần số góc của mạch dao động là: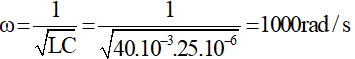

q và i vuông pha nhau nên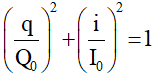

Câu 5: Một mạch dao động gồm tụ điện có điện dung C = 25 nF và cuộn dây thuần cảm có độ tự cảm L = 4 mH. Giả sử ở thời điểm ban đầu cường độ dòng điện đạt giá trị cực đại và bằng 40 mA. Tìm biểu thức điện áp giữa hai bản tụ.

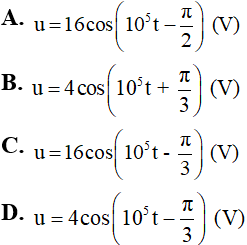
Lời giải:

Hướng dẫn

Chọn A .

Ta có: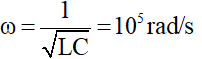

Khi t = 0 thì i = I₀ → cosφi = 1 → φi = 0 → φ_q = φ_u = -π/2 rad.

Mặt khác: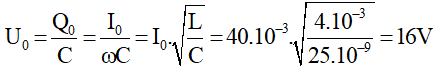

Vậy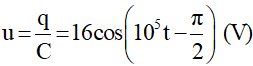

Câu 6: Ba mạch dao động điện từ LC lí tưởng đang có dao động điện từ tự do với các cường độ dòng điện tức thời trong ba mạch lần lượt là i₁ = 4cos4000πt (mA), i₂ = 4cos(4000πt + 0,75π) (mA) và i₃ = 3cos(4000πt + 0,25π) (mA). Tổng điện tích trên ba bản tụ trong ba mạch ở cùng một thời điểm có giá trị lớn nhất bằng

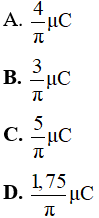
Lời giải:

Hướng dẫn

Chọn D.

Biểu thức điện tích trong ba mạch lần lượt là:

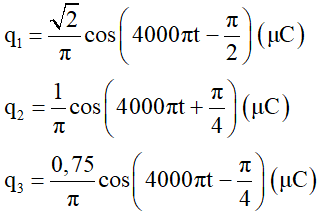
Sử dụng số phức dạng lượng giác, dùng máy tính Casio fx 570VN Plus ta được:

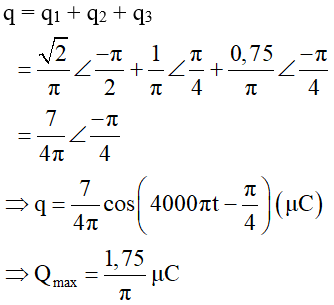
Câu 7:

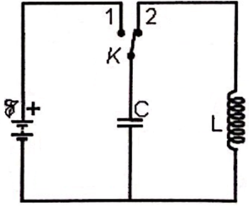
Cho mạch điện như hình vẽ: C = 500 pF; L = 0,2 mH; E = 1,5 V, lấy π² ≈ 10. Tại thời điểm t = 0, khóa K chuyển từ (1) sang (2). Thiết lập công thức biểu diễn sự phụ thuộc của điện tích trên tụ điện C vào thời gian.

A. q = 0,75.cos(10⁶πt + π) nC.

B. q = 0,75.cos(10⁶πt) nC.

C. q = 0,75.cos(10⁶πt – π/2) nC.

D. q = 0,75.sin(10⁶πt – π/2) nC.

Lời giải:

Hướng dẫn

Chọn B.

Ta có: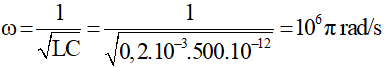

Điện tích cực đại trên tụ: Q₀ = C.U₀ = C.E = 500.10^-12.1,5 = 0,75.10^-9 C.

Vì lúc đầu q = +Q₀ nên q = 0,75.cos(10⁶πt) nC.

Câu 8: Một mạch dao động gồm một tụ điện có điện dung C và cuộn cảm có độ tự cảm L = 0,1 mH, điện trở thuần của mạch bằng không. Biết biểu thức dòng điện trong mạch là: i = 0,04.cos(2.10⁷t) (A). Biểu thức hiệu điên thế giữa hai bản tụ là:

A. u = 80.cos(2.10⁷t) (V)

B. u = 80.cos(2.10⁷t – π/2) V

C. u = 80.cos(2.10⁷t) (nV)

D. u = 10.cos(2.10⁷t + π/2) (nV)

Lời giải:

Hướng dẫn

Chọn B.

Ta có: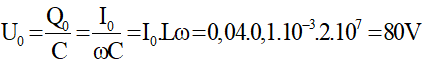

Vì u trễ pha hơn i góc π/2 nên u = 80.cos(2.10⁷t – π/2) V.

Câu 9: Trong một mạch dao động LC lí tưởng, tụ điện có điện dung C và cuộn cảm thuần có độ tự cảm L. Dòng điện trong mạch có giá trị cực đại I₀. Trong khoảng thời gian từ cường độ dòng điện qua cuộn cảm bằng không đến lúc đạt giá trị cực đại, điện lượng đã phóng qua cuộn dây là

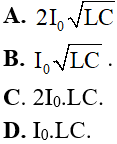
Lời giải:

Hướng dẫn

Chọn B.

Ta có: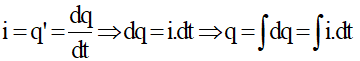

Chọn gốc thời gian là lúc i = 0 và đang tăng, suy ra i = I₀sinωt (A)

Điện lượng đã phóng qua cuộn dây là:

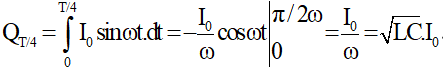
Câu 10: Mạch dao động LC lí tưởng có C = 2nF, đang thực hiện dao động điện từ tự do với chu kỳ T. Tại thời điểm nào đó dòng điện trong mạch có cường độ 4π (mA) và đang tăng, sau đó khoảng thời gian 5T/4 thì hiệu điện thế bản tụ có độ lớn 2 (V). Tần số dao động điện từ của mạch bằng

A. 10 MHz.

B. 400 kHz.

C. 500 kHz.

D. 250 kHz.

Lời giải:

Hướng dẫn

Chọn C.

Tại thời điểm t₁ bất kỳ, ta luôn có i₁ và u1 vuông pha nhau →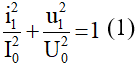

Tại thời điểm t₁ + 5T/4, u1 và u2 vuông pha nhau →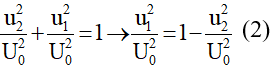

Từ (1) và (2) →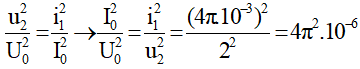

Mặt khác:

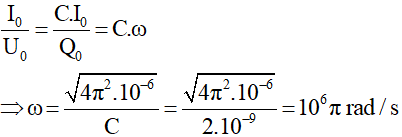
→ Tần số: f = ω /2π = 500000 Hz = 500 kHz.

Câu 11: Mạch dao động LC lí tưởng có L = 5 µH, C = 8 nF. Tại thời điểm t₁, tụ điện có điện tích q₁ = 0,024 µC và đang phóng điện. Tại thời điểm t₂ = t₁ + π (µs) hiệu điện thế giữa hai bản tụ là bao nhiêu?

A. -3 V.

B. 3 V.

C. -5 V.

D. 5 V.

Lời giải:

Hướng dẫn

Chọn A.

Chu kỳ dao động của mạch LC là:

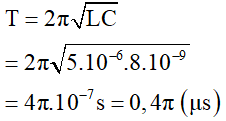
Ta thấy t₂ – t₁ = π (μs) = 2.T + T/2, do đó hai thời điểm t₁ và t₂ là ngược pha.

Suy ra: q₂ = -q₁ = -0,024 μC = -0,024.10^-6C.

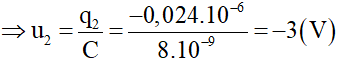
Câu 12: Mạch dao động LC lí tưởng thực hiện dao động điện từ tự do với điện áp cực đại trên tụ là 12 V. Tại thời điểm điện tích trên tụ có giá trị q = 6.10^-9 C thì cường độ dòng điện qua cuộn dây là i = mA. Biết cuộn dây có độ tự cảm 4 mH. Tần số góc của mạch là:

A. 5.10⁴ rad/s.

B. 5.10⁵ rad/s.

C. 25.10⁵ rad/s.

D. 25.10⁴ rad/s.

Lời giải:

Hướng dẫn

Chọn B.

q và i vuông pha nhau nên ta có: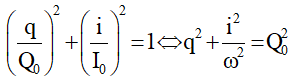

Mà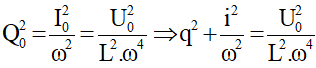

Đặt X = 1/ω₂ ta được: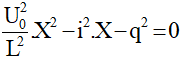

Thay q = 6.10^-9 C; U₀ = 12V; i = mA = 10^-3 A vào và giải phương trình bậc hai ta được: X = 4.10^-12 → ω = 5.10⁵ rad/s.

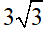
Câu 13: Một mạch dao động LC lí tưởng gồm cuộn cảm thuần L và tụ điện có hai bản A và B. Trong mạch đang có dao động điện từu tụ do với chu kì T, biên độ điện tích của tụ điện bằng Q₀. Tại thời điểm t, điện tích của bản A là q_A = Q₀/3 đang tăng, sau khoảng thời gian ∆t nhỏ nhất thì điện tích của bản B là q_B = Q₀/2. Tỉ số ∆t/T bằng

A. 1/3.

B. 0,53.

C. 0,44.

D. 1/2.

Lời giải:

Hướng dẫn

Chọn B.

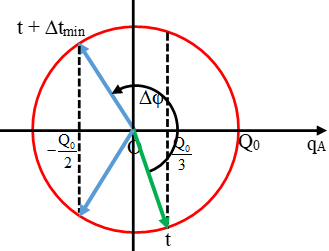
Hai bản A và B của cùng 1 tụ điện luôn có điện tích trái dấu nhau.

Do vậy ở thời điểm t + ∆t khi q_B = Q₀/2 thì q_A = - Q₀/2.

Sử dụng vòng tròn lượng giác biểu diễn q_A.

Ta thấy ∆t_min ứng với góc quay:

Câu 14:

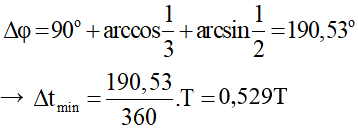
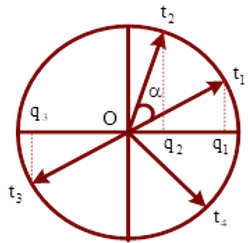
Hai mạch dao động điện từ LC lí tưởng đang có dao động điện từ tự do với các cường độ dòng điện tức thời trong hai mạch là i₁ và i₂ được biểu diễn như hình vẽ. Tổng điện tích của hai tụ điện trong hai mạch ở cùng một thời điểm có giá trị lớn nhất bằng:

A. 5/π (µC).

B. 3/π (µC).

C. 4/π (µC).

D. 2,5/π (µC).

Lời giải:

Hướng dẫn

Chọn D.

Từ đồ thị ta thấy hai dao động này vuông pha nhau, giả sử đường biểu diễn i₁ có biên độ I₀₁ = 4mA, đường còn lại là i₂¬.

Dựa vào thời điểm t = 0, suy ra: i₁ = 4cosωt(mA); i₂ = 3cos(ωt – π/2) (mA).

Mặt khác ta thấy: T = 1,00 ms = 10^-3s → ω = 2000π rad/s.

Điện tích của 2 tụ trong hai mạch tương ứng là:

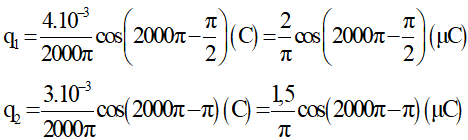
Sử dụng số phức dạng lượng giác, dùng máy tính Casio fx 570VN Plus ta được:

Tổng điện tích của hai tụ điện trong hai mạch ở cùng một thời điểm là:

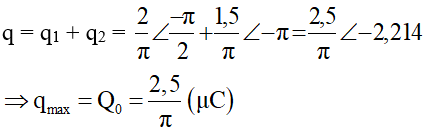
Câu 15: Xét hai mạch dao động điện từ lí tưởng. Chu kì dao động riêng của mạch thứ nhất là T1, của mạch thứ hai là T2 = 2T1. Ban đầu điện tích trên mỗi bản tụ điện có độ lớn cực đại Q₀. Sau đó mỗi tụ điện phóng điện qua cuộn cảm của mạch. Khi điện tích trên mỗi bản tụ của hai mạch đều có độ lớn bằng q (0 < q < Q₀) thì tỉ số độ lớn cường độ dòng điện trong mạch thứ nhất và độ lớn cường độ dòng điện trong mạch thứ hai là:

A. 1/4.

B. 1/2.

C. 4.

D. 2.

Lời giải:

Hướng dẫn

Chọn D.

Trong mỗi mạch q và i vuông pha nhau nên ta có: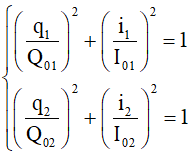

Vì q₁ = q₂ = q, Q₀₁ = Q₀₂ = Q₀ nên suy ra:

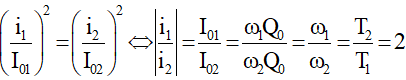
Câu 16: Có hai mạch dao động điện từ lý tưởng đang có dao động điện từ tự do. Ở thời điểm t, gọi q₁ và q₂ lần lượt là điện tích của tụ điện trong mạch dao động thứ nhất và thứ hai. Biết 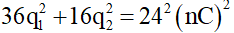. Ở thời điểm t = t₁, trong mạch dao động thứ nhất: điện tích của tụ điện q₁ = 2,4nC; cường độ dòng điện qua cuộn cảm i₁ = 3,2mA. Khi đó, cường độ dòng điện qua cuộn cảm trong mạch dao động thứ hai là:

A. i₂ = 5,4mA.

B. i₂ = 3,2mA.

C. i₂ = 6,4mA.

D. i₂ = 4,5mA

Lời giải:

Hướng dẫn

Chọn B.

Từ biểu thức: 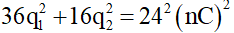(1)

Ta lấy đạo hàm hai vế theo thời gian, ta được: 2.36q₁.i₁ + 2.16.q₂.i₂ = 0.(chú ý q₁, q₂ là hàm của thời gian)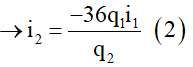

Theo lí thuyết, ta thay các giá trị q₁ và i₁ vào biểu thức (1) ta được: q₂ = 5,5.10^-9C.

Thế q₂ vào (2) ta được: i₂ = 3,2mA.

Câu 17: Trong mạch dao động LC lý tưởng, tụ điện phẳng có điện dung 5 nF, khoảng cách giữa hai bản tụ điện là 4 mm. Điện trường giữa hai bản tụ điện biến thiên theo thời gian với phương trình: E = 1000cos5000t (kV/m) (với t đo bằng giây). Cường độ dòng điện cực đại là:

A. 0,1A. B. mA. C. mA. D. 0,1 mA.

Lời giải:

Hướng dẫn

Chọn A.

Ta có: E = 1000cos5000t (kV/m) → E₀ = 1000.103 V/m; ω = 5000 rad/s.

(1)

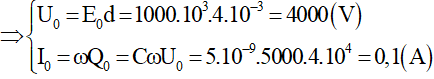
Câu 18: Một mạch dao động điện từ LC lý tưởng. Điện tích cực đại trên bản tụ là Q₀; điện tích tức thời trên mỗi bản tụ là q. Trong một chu kỳ, khoảng thời gian mà q ≥ 0,5Q₀ là 0,1 µs. Chu kỳ dao động của mạch là

A. 0,1 µs

B. 0,3 µs

C. 0,6 µs

D. 1,2 µs.

Lời giải:

Hướng dẫn

Chọn B.

(1)

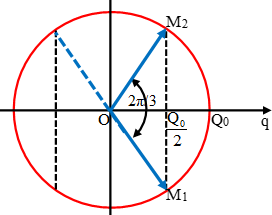
Sử dụng vòng tròn lượng giác biểu diễn q, ta thấy tròng một chu kỳ, khoảng thời gian mà q ≥ 0,5Q₀ ứng với cung M₁OM₂, tưng ứng với góc quét ∆φ = 2π/3.

↔∆t = T/3 = 0,1μs → T = 0,3μs.

Câu 19: Trong mạch dao động LC lí tưởng có dao động điện từ tự do. Ban đầu tụ được tích điện đến giá trị xác định. Trong khoảng thời gian T/4 đầu tiên, tỉ lệ lượng điện tích do tụ phóng ra lần lượt trong ba khoảng thời gian liên tiếp bằng nhau là

(1)

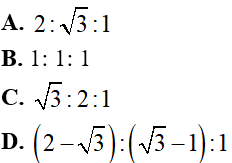
Lời giải:

Hướng dẫn

Chọn D.

Ba khoảng thời gian liên tiếp bằng nhau (∆t₁ = ∆t₂ = ∆t₃ = T/12) trong T/4 đầu tiên tương ứng với 3 góc quay bằng nhau là π/6.

Do vậy:

+ Tại

(1)

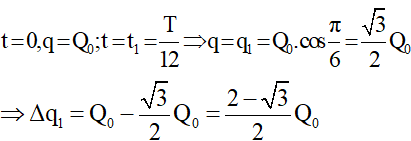
+ Tại

(1)

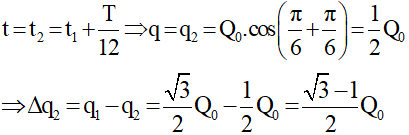
+ Tại

(1)

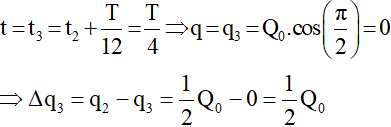
Vậy ta có tỷ lệ:

(1)

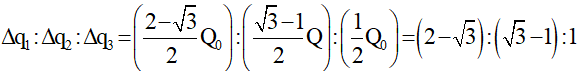
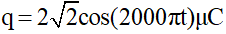
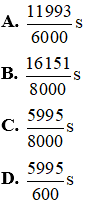
Câu 20: Trong một mạch dao động LC không có điện trở thuần, điện tích trên tụ biến thiên theo phương trình . Kể từ thời điểm ban đầu, điện tích trên tụ có giá trị bằng lần thứ 2019 và đang tăng tại thời điểm:

(1)

Lời giải:

Hướng dẫn

Chọn B.

(1)

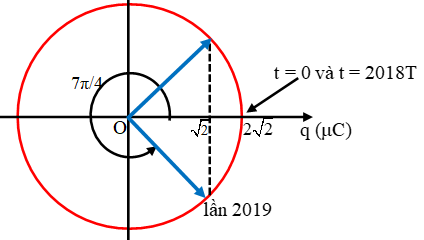
Chu kỳ dao động: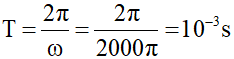

Sử dụng vòng tròn lượng giác biểu diễn q, ta thấy trong 1 chu kỳ T chỉ có 1 thời điểm 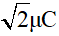và đang tăng ứng với góc quét 7π/4 từ t = 0.

Vậy lần thứ 2019 mất khoảng thời gian là:

(1)

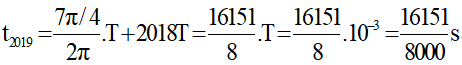
Câu 21: Cho mạch dao động điện từ lý tưởng LC. Biểu thức dòng điện qua cuộn dây có dạng 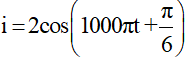(mA). Kể từ t = 0, thời điểm mà cường độ dòng điện qua cuộn dây có độ lớn 1mA lần thứ 2019 là:

(1)

Lời giải:

Hướng dẫn

Chọn A.

(1)

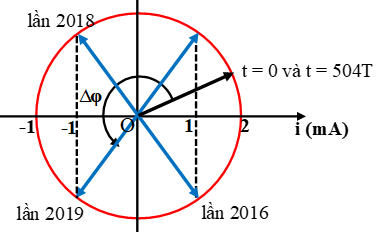
Chu kỳ dao động: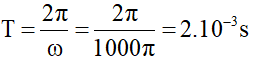

Sử dụng vòng tròn lượng giác biểu diễn i, ta thấy trong 1 chu kỳ T có 4 thời điểm i có độ lớn 1mA.

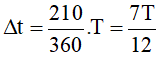
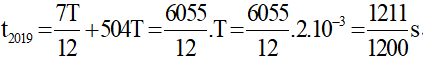
Như vậy sau 504T có 2016 lần i có độ lớn 1mA, để có lần thứ 2019 thì ta phải quét thêm 1 góc ∆φ = 30^o + 180^o = 210^o (ứng với khoảng thời gian ). Vậy:

(1)

Câu 22 (ĐH 2015): Hai mạch dao động điện từ lý tưởng đang có dao động điện từ tự do với cùng cường độ dòng điện cực đại I₀. Chu kỳ dao động riêng của mạch thứ nhất là T1 và của mạch thứ hai là T₂ = 2T₁. Khi cường độ dòng điện trong hai mạch có cùng cường độ và nhỏ hơn I₀ thì độ lớn điện tích trên một bản tụ điện của mạch dao động thứ nhất là q₁ và của mạch dao động thứ hai là q₂. Tỉ số q₁/q₂ là:

A. 2

B. 1,5

C. 0,5

D. 2,5

Lời giải:

Hướng dẫn

Chọn C.

Trong mỗi mạch q và i vuông pha nhau nên ta có: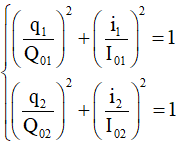

Vì │i₁│= │i₂│, I₀₁ = I₀₂ = I₀ nên suy ra:

(1)

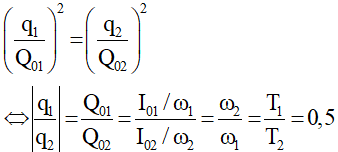
Câu 23: Hai mạch dao động điện từ tự do L₁, C₁ và L₂, C₂; các cuộn dây thuần cảm. Trước khi ghép với các cuộn dây, tụ C₁ đã được tích điện đến giá trị cực đại Q₀₁ = 8μC, tụ C₂ đã được tích điện đến giá trị cực đại Q₀2 = 10μC. Trong quá trình dao động luôn có q₁/i₁=q₂/i₂ , với q₁ và q₂ lần lượt là điện tích tức thời trên tụ C₁ và C₂; i₁ và i₂ lần lượt là cường độ dòng điện tức thời chạy qua cuộn dây L₁ và L₂. Khi q₁ = 6μC thì độ lớn q₂ bằng

A. 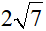μC

B. 7,5μC

C. 6μC

D. 8μC.

Lời giải:

Hướng dẫn

Chọn B.

Cách 1: Ta luôn có: 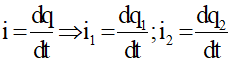(1)

Trong suốt quá trình dao động của hai mạch ta luôn có: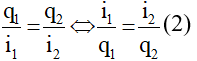

Thay (1) vào (2) ta được: 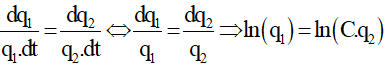(C là hằng số).

Do đó: q₁ = C.q₂.

Tại thời điểm t = 0, q₁ = Q₀1 = 8μC; q₂ = Q₀2 = 10μC → C = 8/10 = 4/5.

Tại thời điểm t, q₁ = 6μC thì .

Lưu ý: Hàm số logarit Nêbe y = lnx có đạo hàm y’ = 1/x nên có vi phân: dy = dx/x.

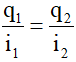
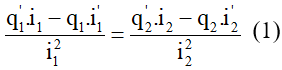
Cách 2:Ta đạo hàm cả hai vế của theo thời gian. Khi đó ta được:

μC

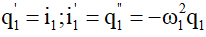
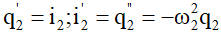
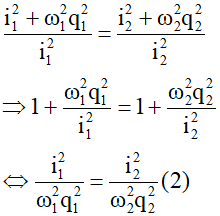
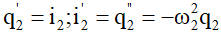
Ta thay và vào (1), ta được:

và vào (1), ta được:

Mặt khác sử dụng công thức độc lập ta có:

và vào (1), ta được:

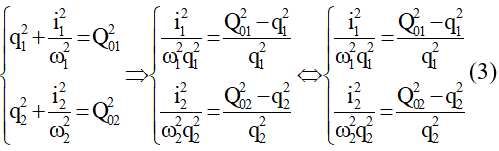
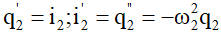
Từ (2) và (3) suy ra: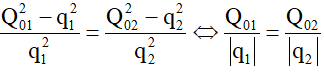

Thay Q₀1 = 8μC; Q₀2 = 10μC và q₁ = 6μC vào ta tìm được │q₂│= 7,5μC.

Câu 24: Cho 3 mạch dao động tự do LC dao động với tần số khác nhau. Biết điện tích cực đại trên các tụ đều bằng 5μC. Biết rằng tại mọi thời điểm, điện tích trên tụ và cường độ dòng trên các mạch liên hệ với nhau bằng biểu thức 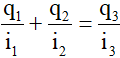, với q₁, q₂, q₃ lần lượt là điện tích trên tụ của mạch 1, mạch 2, mạch 3; i₁, i₂, i₃ lần lượt là cường độ dòng trên mạch 1, mạch 2, mạch 3. Tại thời điểm t, điện tích trên tụ của mạch 1, mạch 2 và mạch 3 lần lượt là 2 μC, 3 μC và q₀. Giá trị của q₀ gần giá trị nào nhất sau đây?

A. 1μC

B. 2μC

C. 4μC

D. 3μC

Lời giải:

Hướng dẫn

Chọn C.

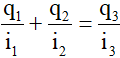
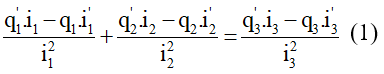
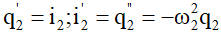
Ta đạo hàm cả hai vế của theo thời gian. Khi đó ta được:

và vào (1), ta được:

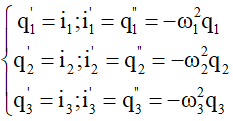
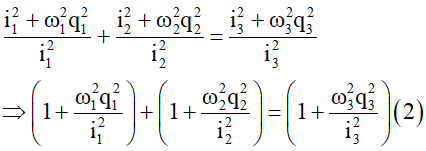
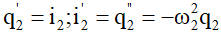
Ta thay vào (1), ta được:

và vào (1), ta được:

Mặt khác sử dụng công thức độc lập ta có:

và vào (1), ta được:

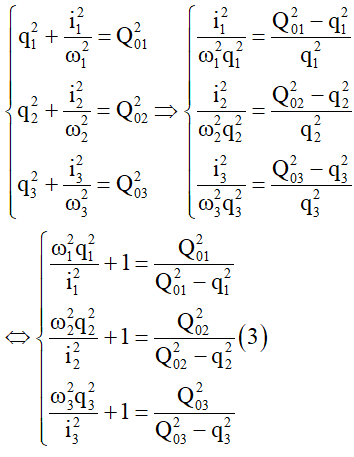
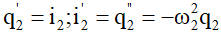
Từ (2) và (3) suy ra: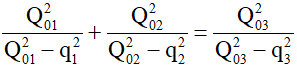

Thay Q₀₁ = Q₀₂ = Q₀₃ = 5μC và q₁ = 2μC, q₂ = 3μC vào ta tìm được│q₃│= 3,99μC.

Câu 25:

và vào (1), ta được:

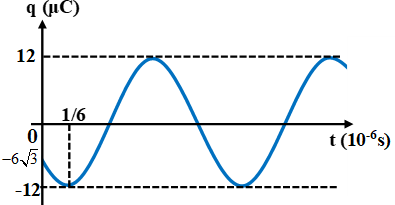
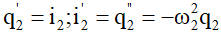
Điện tích trên tụ trong mạch dao động LC lí tưởng có đồ thị như hình vẽ. Phương trình dòng điện chạy trong mạch có dạng

và vào (1), ta được:

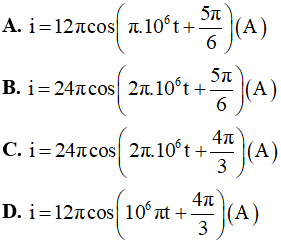
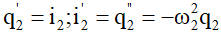
Lời giải:

Hướng dẫn

Chọn D.

và vào (1), ta được:

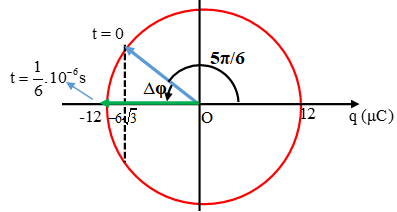
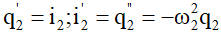
Từ đồ thị ta thấy Q₀ = 12μC.

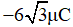
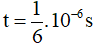
Tại t = 0 thì q = và đang giảm, tại thì q = -Q₀ lần đầu tiên.

Sử dụng vòng tròn lượng giác biểu diễn q ta được:

và vào (1), ta được:

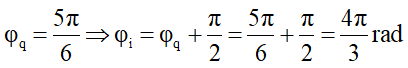
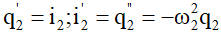
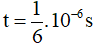
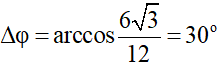
Từ t = 0 đến ứng với góc quét: tương ứng với khoảng thời gian là T/12.

Suy ra 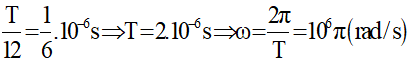→ I₀ = ωQ₀ = 12π (A).

Vậy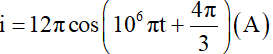

Câu 26: Một mạch dao động lý tưởng đang thực hiện dao động điện từ tự do, điện tích trên một bản tụ điện biến thiên theo phương trình. Trong ba khoảng thời gian theo thứ tự liên tiếp nhau là Δt₁ = 0,5μs; Δt₂ = Δt₃ = 1μs thì điện lượng chuyển qua tiết diện ngang của dây dẫn tương ứng là Δq₁ = 3.10^-6C; Δq₂ = 9.10^-6C; Δq₃. Δq₃ nhận giá trị nào sau đây ?

A. Δq₃ = 9.10^-6C

B. Δq₃ = 6.10^-6C

C. Δq₃ = 12.10^-6C

D. Δq₃ = 15.10^-6C

Lời giải:

Hướng dẫn

Chọn D.

Điện lượng chuyển qua tiết diện bằng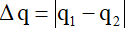

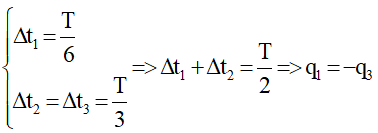
* Trường hợp 1:

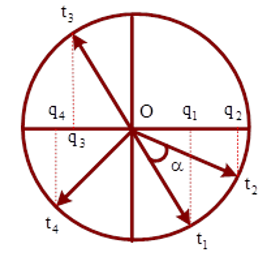
Nếu q₁ < q₂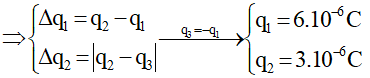

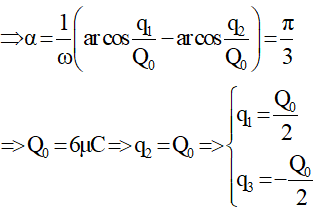
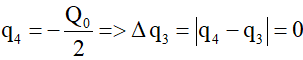
(Loại trường hợp này)

* Trường hợp 2 :

(Loại trường hợp này)

Nếu q₁ > q₂

(Loại trường hợp này)