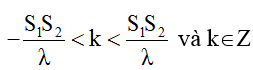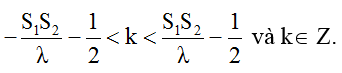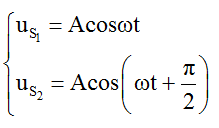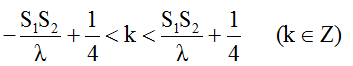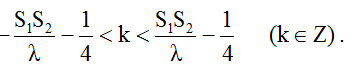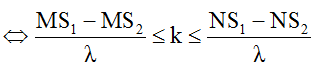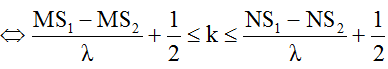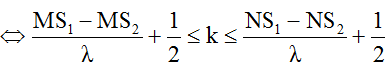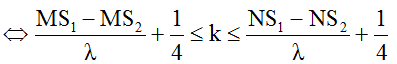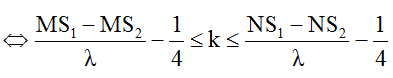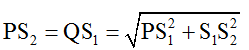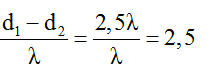Cách tìm số điểm dao động cực đại, cực tiểu giữa hai nguồn, hai điểm bất kì trong giao thoa sóng hay, chi tiết - Vật Lí lớp 12
Cách tìm số điểm dao động cực đại, cực tiểu giữa hai nguồn, hai điểm bất kì trong giao thoa sóng hay, chi tiết
Với Cách tìm số điểm dao động cực đại, cực tiểu giữa hai nguồn, hai điểm bất kì trong giao thoa sóng hay, chi tiết Vật Lí lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm số điểm dao động cực đại, cực tiểu giữa hai nguồn, hai điểm bất kì trong giao thoa sóng từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

A. Phương pháp giải
1. Tìm số điểm dao động cực đại và cực tiểu giữa hai nguồn S1, S2 cùng pha
Các công thức:
* Số cực đại giữa hai nguồn:
* Số cực tiểu giữa hai nguồn:
B. Ví dụ minh họa
Ví dụ 1: Trong một thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn kết hợp S1 và S2 cách nhau 10 cm dao động cùng pha và có bước sóng 2 cm. Coi biên độ sóng không đổi khi truyền đi. Tìm số điểm dao động với biên độ cực đại, số điểm dao động với biên độ cực tiểu quan sát được trên khoảng nối giữa hai nguồn.
Hướng dẫn giải:
Vì các nguồn dao động cùng pha nên ta có số đường hoặc số điểm dao động cực đại:
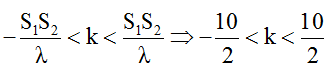
=> – 5 < k < 5.
Suy ra: k = 0; ±1; ±2 ;±3; ±4.
Vậy có 9 số điểm (đường) dao động cực đại.
Ta có số đường hoặc số điểm dao động cực tiểu:
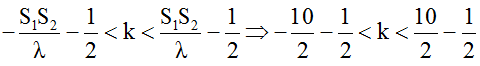
=> – 5,5 < k < 4,5.
Suy ra: k = 0; ± 1;±2 ;±3; ±4; - 5.
Vậy có 10 số điểm (đường) dao động cực tiểu.
2. Tìm số điểm dao động cực đại và cực tiểu giữa hai nguồn S1, S2 ngược pha: (∆φ = φ1 – φ2 = π)
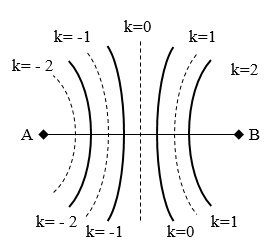
* Điểm dao động cực đại: d1 – d2 = (2k+1)λ/2 (k∈Z)
Số đường hoặc số điểm dao động cực đại (không tính hai nguồn): 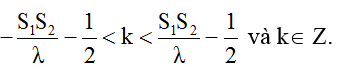
* Điểm dao động cực tiểu (không dao động): d1 – d2 = kl (k∈Z)
Số đường hoặc số điểm dao động cực tiểu (không tính hai nguồn): 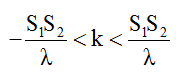
Ví dụ 2: Hai nguồn kết hợp A và B cách nhau 50mm lần lượt dao động theo phương trình u1 = acos200πt(cm) và u2 = acos(200πt + π )(cm) trên mặt thoáng của thuỷ ngân. Xét về một phía của đường trung trực của AB, người ta thấy vân bậc k đi qua điểm M có MA – MB = 12mm và vân bậc (k + 3) (cùng loại với vân bậc k) đi qua điểm N có NA – NB = 36mm. Số điểm cực đại giao thoa trên đoạn AB là
A. 12. B. 13. C. 11. D. 14.
Hướng dẫn giải:
Chọn A
Vì hai nguồn ngược pha nên điều kiện cực tiểu cho điểm bất kỳ: d1 – d2 = kλ và vân cực tiểu có bậc k.
Ta có: MA – MB = 12mm = kλ; NA – NB = 36mm = (k + 3)λ
→ 3λ = 36 – 12 = 24mm → λ = 8mm.
Số điểm dao động cực đại (không tính hai nguồn) trên đoạn AB được xác định như sau:
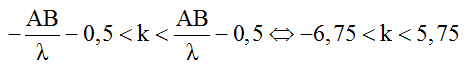
Vì k ∈ Z nên k = -6; -5; ...;-1; 0; 1; ...; 5. Vậy có 12 điểm cực đại giao thoa trên AB.
3. Tìm số điểm dao động cực đại và cực tiểu giữa hai nguồn vuông pha ∆φ = (2k+1)π/2 (Số cực đại = Số cực tiểu)
+ Phương trình hai nguồn kết hợp:
+ Phương trình sóng tổng hợp tại M:
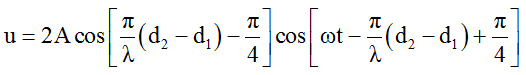
+ Biên độ sóng tổng hợp: 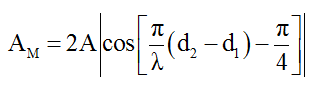
+ Tìm số điểm dao động cực đại, số điểm dao động cực tiểu:
* Số cực đại:
* Số cực tiểu:
Nhận xét: số điểm cực đại và cực tiểu trên đoạn AB là bằng nhau nên có thể dùng 1 công thức là đủ => Số giá trị nguyên của k thoả mãn các biểu thức trên là số đường cần tìm.
Ví dụ 3: Trên mặt nước có hai nguồn kết hợp S1, S2 cách nhau 10(cm) dao động theo các phương trình: u1 = 0,2cos(50πt + π) cm và u2 = 0,2cos(50πt + π/2) cm. Biết vận tốc truyền sóng trên mặt nước là 0,5(m/s). Tính số điểm cực đại và cực tiểu trên đoạn S1S2.
A. 8 và 8 B. 9 và 10 C. 10 và 10 D. 11 và 12
Hướng dẫn giải:
Chọn C.
Bước sóng: λ = v/f = 0,5/25 = 0,02m = 2cm
Số điểm dao động cực đại, số điểm dao động cực tiểu:
* Số cực đại:
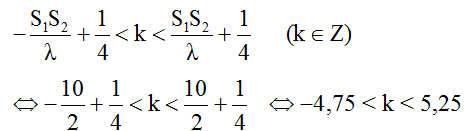
Vì k ∈ Z nên k = -4; -3; ...;-1; 0; 1; ...; 5. Vậy có 10 điểm cực đại giao thoa trên S1S2.
* Số cực tiểu:
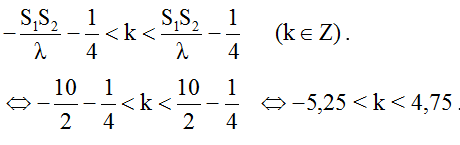
Vì k ∈ Z nên k = -5; -4; ...;-1; 0; 1; ...; 4. Vậy có 10 điểm cực tiểu giao thoa trên S1S2.
4. Tìm số điểm dao động với biên độ cực đại, cực tiểu giữa hai điểm bất kỳ hoặc trên một đường với dạng hình học đã biết.
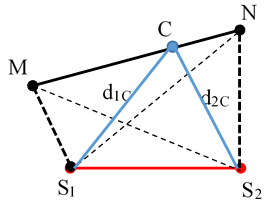
Các bài toán trên luôn sử dụng bài toán tìm số cực đại và cực tiểu trên đoạn thẳng nối hai điểm M và N trong vùng có giao thoa (M gần S1 hơn S2 còn N thì xa S1 hơn S2), đó là số các giá trị của k (k ∈ Z) tính theo công thức sau (không tính hai nguồn):
* C dao động cực đại khi độ lệch pha của hai sóng từ hai nguồn tại C thỏa mãn:
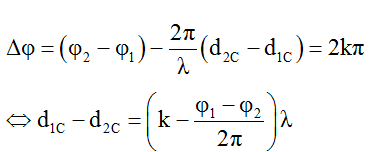
Số cực đại C trên đoạn MN được xác định như sau:
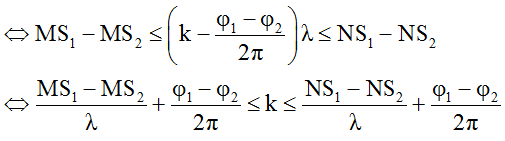
* Tương tự số cực tiểu C trên đoạn MN được xác định như sau:
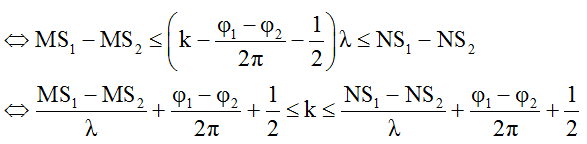
Ta suy ra các công thức cho các trường hợp đặc biệt sau đây:
+ Hai nguồn dao động cùng pha: (φ1 – φ2 = 0)
* Số cực đại:
* Số cực tiểu:
+ Hai nguồn dao động ngược pha: (φ1 – φ2 = (2m + 1)π )
* Số cực đại:
* Số cực tiểu: 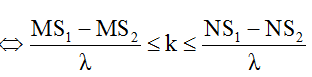
+ Hai nguồn dao động vuông pha: (φ1 – φ2 = (2m + 1)π/2)
* Số cực đại:
* Số cực tiểu:
Chú ý: Trong các công thức trên nếu M hoặc N trùng với nguồn thì không dùng dấu “=” (chỉ dùng dấu <) Vì nguồn là điểm đặc biệt không phải là điểm cực đại hoặc cực tiểu.
a) Xác định số điểm cực đại, cực tiểu trên đoạn thẳng PQ tạo với hai nguồn S1, S2 một hình vuông hoặc hình chữ nhật.
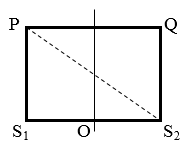
* Số điểm cực đại trên đoạn PQ thoã mãn:
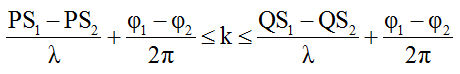
Trong đó:
Giải bất phương trình suy ra số giá trị k ∈ Z bằng số điểm cực đại trên đoạn PQ.
* Số điểm cực tiểu trên đoạn CD thoã mãn:
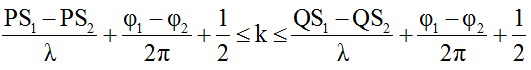
Giải bất phương trình suy ra số giá trị k ∈ Z bằng số điểm cực tiểu trên đoạn PQ.
Ví dụ 4: Ở mặt thoáng của một chất lỏng có hai nguồn kết hợp A và B cách nhau 20 cm dao động theo phương thẳng đứng với phương trình uA = 2cos40πt mm và uB = 2cos(40πt + π) mm Biết tốc độ truyền sóng trên mặt chất lỏng là 30 cm/s. Xét hình vuông ABCD thuộc mặt chất lỏng. Số điểm dao động với biên độ cực đại trên đoạn CD là:
A. 12 B. 18 C. 15 D. 20
Hướng dẫn giải:
Chọn A.
Số điểm cực đại trên đoạn CD thoã mãn:
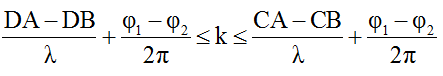
Trong đó: φ1 = 0, φ2 = π, DB = CA = AB√2 = 20√2 cm ; DA = CB = AB = 20cm;
Bước sóng λ = v/f = 30/20 = 1,5cm.
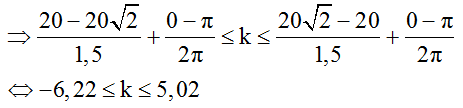
Vì k ∈ Z nên k = -6; -5; ...;-1; 0; 1; ...; 5. Vậy có 12 điểm cực đại giao thoa trên CD.
b) Xác định số điểm cực đại, cực tiểu trên đoạn thẳng là đường chéo của một hình vuông hoặc hình chữ nhật.
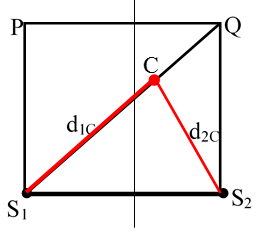
Xác định số điểm dao động cực đại, cực tiểu trên đoạn S1Q, biết PQS2S1 là hình vuông với S1, S2 là hai nguồn.
* Giả sử tại C dao động cực đại, số điểm C được xác định như sau:
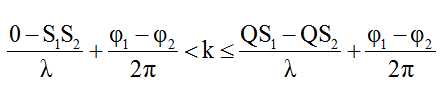
(vế trái ta dùng dấu “ < “ do trên đoạn S1Q có S1 trùng với nguồn)
Giải bất phương trình suy ra số giá trị k ∈ Z bằng số điểm cực đại trên đoạn S1Q.
* Tương tự ta tìm được số điểm cực tiểu trên đoạn S1Q qua điều kiện sau:
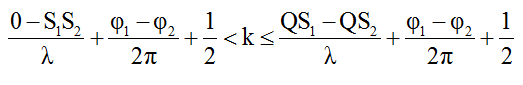
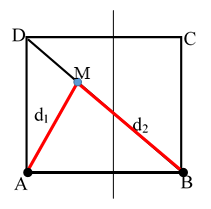
Ví dụ 5: Ở mặt thoáng của một chất lỏng có hai nguồn kết hợp A và B cách nhau 20 cm dao động theo phương thẳng đứng với phương trình uA = 2cos40πt mm và uB = 2cos(40πt + π/2) Biết tốc độ truyền sóng trên mặt chất lỏng là 30 cm/s. Xét hình vuông ABCD thuộc mặt chất lỏng. Số điểm dao động với biên độ cực đại trên đoạn BD là:
A. 17 B. 18 C. 19 D. 20
Hướng dẫn giải:
Chọn C.
Số điểm cực đại trên đoạn BD được xác định như sau:
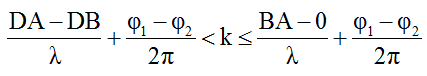
Trong đó: bước sóng λ = v/f = 30/20 = 1,5cm; φ1 = 0; φ2 = π/2; DA = BA = 20cm; DB = 20√2 cm
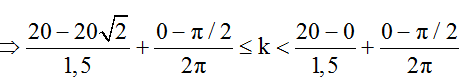
=> -5,77 ≤ k ≤ 13,08
Vì k ∈ Z nên k = -5; -4; ...;-1; 0; 1; ...; 13. Vậy có 19 điểm cực đại giao thoa trên BD
c) Xác định số điểm cực đại, cực tiểu trên đường thẳng vuông góc với hai nguồn S1S2.
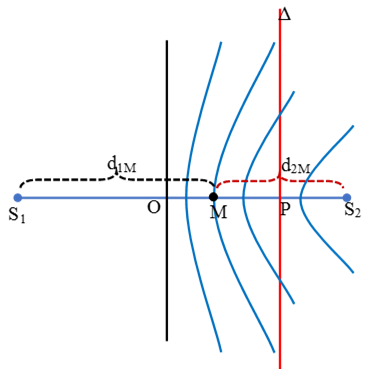
* Số điểm dao động cực đại trên đường ∆ vuông góc với S1S2 tại điểm P xác định chính là số giao điểm của các đường Hyperpol cực đại trong đoạn OP (không tính điểm O nếu có) với ∆.
Do vậy ta quy bài toán về bài toán tìm số cực đại trên đoạn OP, sau đó tìm số giao điểm của các đường Hyperpol đi qua các điểm cực đại trên với ∆.
Số điểm M dao động cực đại trên OP được xác định như sau:
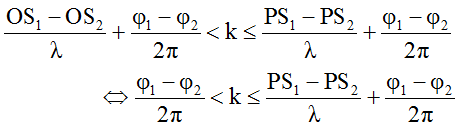
↔ m1 < k ≤ m2.
Giả sử từ bất phương trình trên ta tìm được n giá trị k nguyên.
Lưu ý: Không lấy dấu ‘=’ cho vế trái vì nếu có đường cực đại đi qua O thì nó là đường trung trực không cắt ∆ được. Nếu P trùng với 1 trong hai nguồn thì ta bỏ dấu ‘=’ ở vế phải.
+ Nếu m2 ϵ Z thì có 1 đường cực đại đi qua P tiếp xúc với ∆, do đó số điểm cực đại trên ∆ là Ncđ = 2(n – 1) + 1.
+ Nếu m2 ∉ Z thì không có đường cực nào tiếp xúc với ∆, do đó số điểm cực đại trên ∆ là Ncđ = 2.n.
* Làm tương tự cho trường hợp tìm số điểm cực tiểu trên ∆.
Ví dụ 6: Trên mặt nước có hai nguồn A và B cách nhau 5 cm, có phương trình lần lượt là u1 = acos(ωt - π/2), u2 = acos(ωt + π/2) Trên nửa đường thẳng Bx qua B, vuông góc AB, điểm không dao động cách B xa nhất là 12cm. Tìm tổng số cực đại và cực tiểu trên Bx.
A. 8. B. 9. C. 7. D. 11.
Hướng dẫn giải:
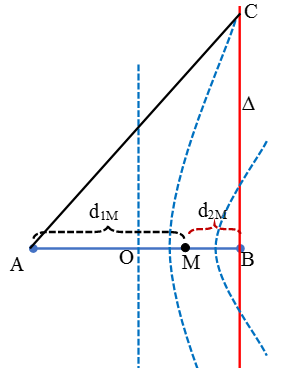
Chọn B.
Vì hai nguồn ngược pha nên đường trung trực của AB là đường cực tiểu bậc 0. Do đó điểm trên Bx không dao động cách B xa nhất là C giao điểm của cực tiểu bậc 1 với Bx.
Ta có:
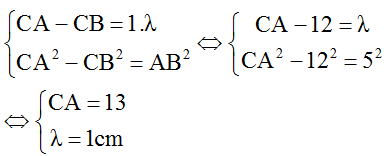
+ Số điểm M dao động cực đại trên OB được xác định như sau:
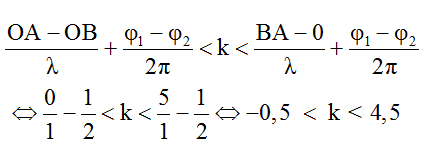
(không lấy dấu bằng ở vế phải vì B là nguồn)
Vì k ∈ Z nên k = 0; 1; ...; 4 nên có 5 điểm cực đại giao thoa trên OB → có 5 cực đại trên tia Bx.
+ Số điểm M dao động cực tiểu trên OB được xác định như sau:
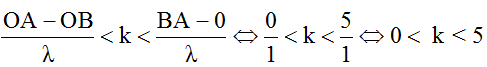
Vì k ∈ Z nên k = 1; ...; 4 nên có 4 điểm cực tiểu giao thoa trên OB → có 4 cực tiểu trên tia Bx.
Vậy tổng số cực đại và cực tiểu trên Bx là 9.
d) Tìm số điểm dao động với biên độ cực đại, cực tiểu tiểu trên đường tròn (hoặc tìm số điểm dao động với biên độ cực đại, cực tiểu trên đường elip, hình chữ nhật, hình vuông, parabol… )
* Phương pháp chung: Ta quy bài toán về bài toán tính số điểm cực đại hoặc cực tiểu trên đoạn MN chứa các đường hyperpol cực đại hoặc cực tiểu luôn cắt các đường biên bao quanh có dạng hình học đã cho. Sau đó ta tìm số giao điểm là xác định được số điểm cần tìm.
Ví dụ nếu đường bao quanh là đường tròn thì số điểm cực đại hoặc cực tiểu trên đường tròn là 2n (n là số điểm tìm được trên đoạn MN, có chú ý tới các trường hợp đặc biệt). Do mỗi đường cong hyperbol cắt đường tròn tại 2 điểm.
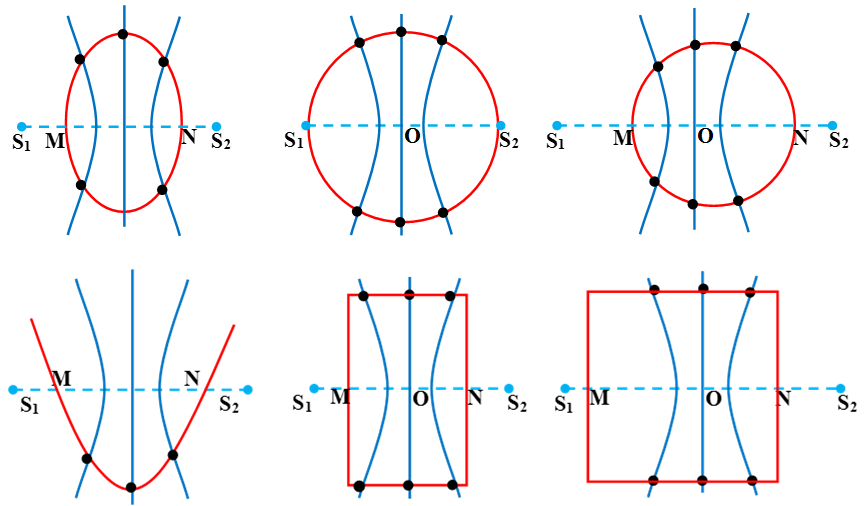
Ví dụ 7: Trên bề mặt chất lỏng cho 2 nguồn S1, S2 dao động vuông góc với bề mặt chất lỏng có phương trình dao động uS1 = 3cos(10πt) cm và uS2 = 3cos(10πt + π/3) cm. Tốc độ truyền sóng trên mặt nước là 50 cm/s. Biết khoảng cách S1S2 là 30 cm. Cho điểm C trên đoạn S1S2, cách S1 khoảng 18cm và cách S2 12 cm. Vẽ vòng tròn đường kính 10 cm, tâm tại C. Số điểm dao động với biên độ cực đại trên đường tròn là:
A. 6 B. 4 C. 8 D. 7
Hướng dẫn giải:
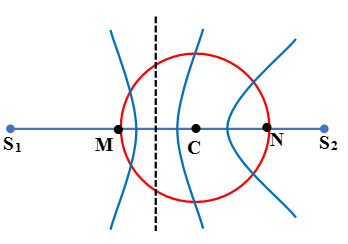
Chọn B.
Số điểm dao động cực đại trên MN (đường kính của đường tròn) được xác định như sau:
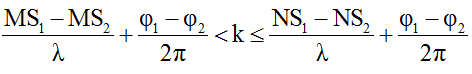
Trong đó:
Bước sóng λ = v/f = 50/5 = 10cm; φ1 = 0, φ2 = π/3.
MS1 = CS1 – MC = 18 – 5 = 13cm.
MS2 = 30 – 13 = 17cm.
NS2 = CS2 – CN = 12 – 5 = 7cm.
NS1 = 30 – 7 = 23cm.
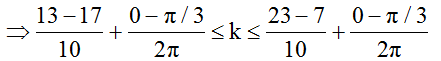
=> -0,57 ≤ k ≤ 1,43
Vì k ∈ Z nên k = 0; 1. Do đó có 2 điểm cực đại giao thoa trên MN tương ứng với hai đường hyperbol cực đại cắt đường tròn tại 4 điểm.
Ví dụ 8: Ở mặt thoáng của một chất lỏng có hai nguồn sóng kết hợp A và B cách nhau 20 cm, dao động theo phương thẳng đứng với phương trình uA = 2cos40πt và uB = 2cos(40πt + π) (uA và uB tính bằng mm, t tính bằng s). Biết tốc độ truyền sóng trên mặt chất lỏng là 30 cm/s. Xét hình vuông ABMN thuộc mặt thoáng chất lỏng. Số điểm dao động với biên độ cực đại trên hình vuông ABMN là:
A. 26. B. 52. C. 37. D. 50.
Hướng dẫn giải:
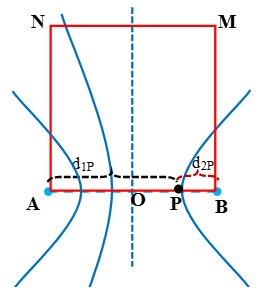
Chọn B.
Ta nhận thấy tất cả các đường hyperbol cực đại trên đoạn nối hai nguồn AB đều cắt hình vuông ABMN tại hai điểm. Do vậy ta quy bài toán về tìm số điểm cực đại trên đoạn AB.
Số điểm dao động cực đại trên AB được xác định như sau:
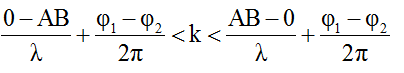
Trong đó λ = v/f = 30/20 = 1,5cm; φ1 = 0, φ2 = π.
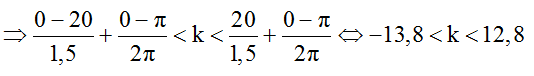
Vì k ∈ Z nên k = -13; -12; ...;-1; 0; 1; ...; 12. Do đó có 26 điểm cực đại giao thoa trên AB tương ứng với 26 đường hyperbol cực đại cắt hình vuông tại 52 điểm.
C. Bài tập vận dụng
Câu 1: Hai nguồn sóng kết hợp A và B dao động ngược pha với tần số f = 40Hz, vận tốc truyền sóng v = 60cm/s. Khoảng cách giữa hai nguồn sóng là 7cm. Số điểm dao động với biên độ cực đại giữa A và B
A. 7. B. 8. C. 10. D. 9.
Lời giải:
Chọn C.
Bước sóng: λ = v/f = 60/40 = 1,5cm.
Hai nguồn sóng kết hợp A và B dao động ngược pha nên số điểm dao động cực đại (không tính hai nguồn) trên đoạn AB được xác định như sau:
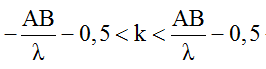
⇔ -5,17 < k < 4,17
Vì k ∈ Z nên k = -5; -4; ...;-1; 0; 1; ...; 4. Vậy có 10 điểm cực đại giao thoa trên AB.
Câu 2: Hai nguồn sóng cùng biên độ cùng tần số và ngược pha. Nếu khoảng cách giữa hai nguồn là: AB = 16,2λ thì số điểm đứng yên và số điểm dao động với biên độ cực đại trên đoạn AB lần lượt là:
A. 32 và 33 B. 34 và 33 C. 33 và 32 D. 33 và 34.
Lời giải:
Chọn C.
Hai nguồn sóng kết hợp A và B dao động ngược pha nên số điểm dao động cực tiểu trên đoạn AB được xác định như sau:
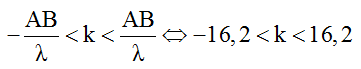
Vì k ∈ Z nên k = -16; -15; ...;-1; 0; 1; ...; 16. Vậy có 33 điểm cực tiểu giao thoa trên AB.
Số điểm dao động cực đại (không tính hai nguồn) trên đoạn AB được xác định như sau:
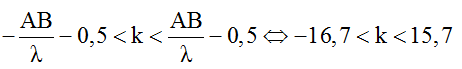
Vì k ∈ Z nên k = -16; -15; ...;-1; 0; 1; ...; 15. Vậy có 32 điểm cực đại giao thoa trên AB.
Câu 3: (ĐH 2009): Ở bề mặt một chất lỏng có hai nguồn phát sóng kết hợp S1 và S2 cách nhau 20cm. Hai nguồn này dao động theo phương trẳng đứng có phương trình lần lượt là u1 = 5cos40 πt (mm) và u2 = 5cos(40 πt + π) (mm). Tốc độ truyền sóng trên mặt chất lỏng là 80 cm/s. Số điểm dao động với biên độ cực đại trên đoạn thẳng S1S2 là:
A. 11. B. 9. C. 10. D. 8.
Lời giải:
Chọn C.
Bước sóng truyền đi trong môi trường λ = v/f = 80/20 = 4cm.
Số điểm dao động cực đại trên đoạn S1S2 được xác định như sau:
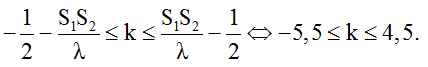
Vì k ∈ Z nên k = -5; -4; ...;-1; 0; 1; ...; 4. Vậy có 10 điểm cực đại giao thoa trên S1S2.
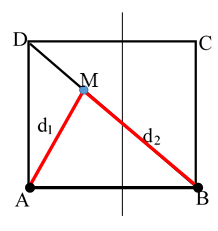
Câu 4: Ở mặt thoáng một chất lỏng có hai nguồn sóng kết hợp A và B cách nhau 20cm, dao động theo phương thẳng đứng với phương trình uA = 2cos40πt và uB = 2cos(40πt + π) (uA và uB tính bằng mm, t tính bằng s). Cho v = 30cm/s. Xét hình vuông ABCD thuộc mặt thoáng chất lỏng. Số điểm dao động với biên độ cực đại trên đoạn BD là:
A.17 B.18 C.19 D.20
Lời giải:
Chọn C.
Số điểm cực đại trên đoạn BD được xác định như sau:
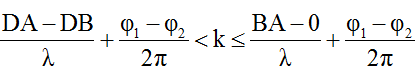
Trong đó: bước sóng λ = v/f = 30/20 = 1,5cm; φ1 = 0; φ2 = π; DA = BA = 20cm; DB = 20√2 cm
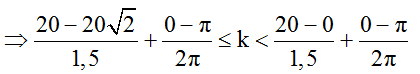
⇔ -6,02 ≤ k ≤ 12,8
(vì B là nguồn nên ta không lấy dấu “=” vế bên phải)
Vì k ∈ Z nên k = -6; -5; ...;-1; 0; 1; ...; 12. Vậy có 19 điểm cực đại giao thoa trên BD.
Câu 5: Hai nguồn kết hợp A, B cách nhau 16 cm đang cùng dao động vuông góc với mặt nước theo phương trình: u = a.cos50πt (cm). Xét một điểm C trên mặt nước không dao động, giữa C và trung trực của AB có một đường cực đại. Biết AC = 17,2cm và BC = 13,6cm. Số đường cực đại đi qua khoảng AC là:
A. 5. B. 6. C. 7. D. 8.
Lời giải:
Chọn D.
Hai nguồn kết hợp cùng pha, điểm C là cực tiểu thì d1C – d2C = (k + 0,5)λ.
Vì giữa C và đường trung trực chỉ có 1 cực đại nên cực tiểu đi qua C có hiệu đường đi bằng 1,5λ hay 1,5λ = AC – BC = 17,2 – 13,6 → λ = 2,4cm.
Cực đại thuộc khoảng AC thỏa mãn
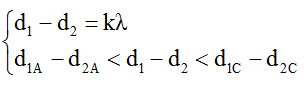
↔ 0 – 16 < 2,4k < 17,2 – 13,6 ↔ -6,7 < k < 1,5
Vì k ∈ Z nên k = -6; -5; ...;-1; 0; 1. Vậy có 8 điểm cực đại giao thoa trên khoảng AC.
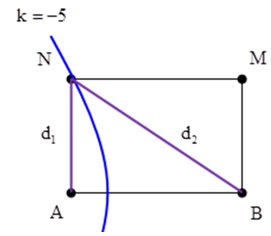
Câu 6: Trên mặt nước, tại hai điểm A và B cách nhau 44 cm có hai nguồn dao động cùng pha theo phương thẳng đứng, phát ra hai sóng kết hợp có bước sóng 8 cm. Gọi M và N là hai điểm trên mặt nước sao cho ABMN là hình chữ nhật. Để trên MN có số điểm dao động với biên độ cực đại nhiều nhất thì diện tích hình chữ nhật ABMN lớn nhất gần giá trị nào nhất sau đây?
A. 260 cm2. B. 180 cm2. C. 180 mm2. D. 260 mm2.
Lời giải:
Chọn B.
Số điểm dao động với biên độ cực đại trên đoạn thẳng nối hai nguồn được xác định như sau:
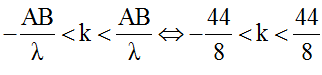
⇔ -5,5 < k < 5,5
+ Để số điểm dao động với biên độ cực đại trên MN là nhiều nhất thì N phải nằm trên hypebol cực đại ứng với k = -5
+ N nằm trên cực đại nên ta có d2 – d1 = 5.λ = 40cm.
Mặc khác:
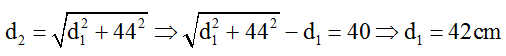
Diện tích của hình chữ nhật: S = AB. AN = 44.4,2 = 184,8cm2.
Câu 7: Tại mặt thoáng của một chất lỏng có hai nguồn kết hợp A và B cách nhau 8 cm. Cho A, B dao động điều hòa, cùng pha, theo phương vuông góc với mặt chất lỏng. Bước sóng của sóng trên mặt chất lỏng là 1 cm. Gọi M, N là hai điểm thuộc mặt chất lỏng sao cho MN = 4cm và AMNB là hình thang cân. Để trên MN có đúng 5 điểm dao động với biên độ cực đại thì diện tích lớn nhất của AMNB là:
A. 9√5 cm2 B. 18√5 cm2 C. 9√3 cm2 D. 18√3 cm2
Lời giải:
Chọn B.
Số điểm dao động với biên độ cực đại trên AB được xác định như sau:
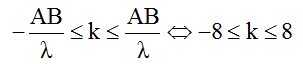
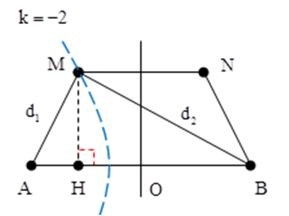
Để diện tích AMNB là lớn nhất thì M phải nằm trên cực đại ứng với k = -2.
Khi đó: d2M – d1M = 2λ = 2cm.
Mặt khác:
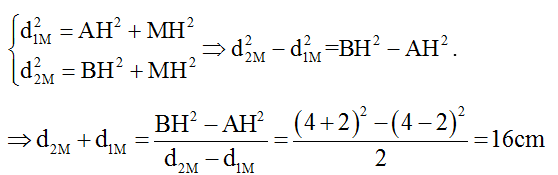
Ta tính được d1M = 7cm, từ đó suy ra MH = 2√5cm
Diện tích hình thang: SMNB = 1/2 (AB + MN).MH = 18√5 cm2.
Câu 8: Trên mặt nước phẳng lặng, hai điểm A và B cách nhau 21 cm, điểm M cách A và B lần lượt là 17 cm và 10 cm. Điểm N đối xứng với M qua đường thẳng AB. Đặt tại A và B hai nguồn sóng dao động theo phương thẳng đứng, cùng biên độ, cùng tần số, cùng pha. Khi đó sóng trên mặt nước có bước sóng bằng 2 cm. Số điểm đứng yên trên đường thẳng MN là
A. 9 B. 11 C. 8 D. 10
Lời giải:
Chọn A.
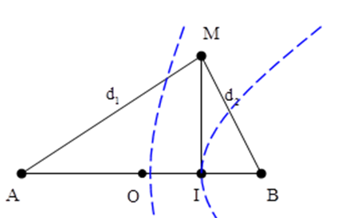
Hai nguồn là kết hợp và cùng pha nên trung điểm O của AB là một cực đại. Cách cực đại này một đoạn λ/4 là cực tiểu thứ nhất. Các cực tiểu liên tiếp cách nhau λ/2.
Từ hình vẽ ta có:
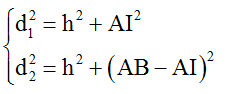
Giải hệ ta thu được AI = 15cm → OI = 4,5cm = (4 + 0,5).λ/2.
Từ O đến I có 5 cực tiểu trong đó cực tiểu thứ năm đi qua I.
→ Số điểm đứng yên trên đường thẳng MN là 9.
Câu 9: Trên mặt nước có hai nguồn kết hợp A và B cách nhau 24 cm, dao động theo phương trình lần lượt là u1 = acos(40πt), u2 = bcos(40πt + π/3). Biết tốc độ truyền sóng là 120cm/s. Gọi M, N là hai điểm trên mặt nước sao cho AMNB là hình chữ nhật với NB = 18cm. Số điểm cực đại và số điểm cực tiểu trên MN lần lượt là:
A. 3 và 3. B. 4 và 4. C. 4 và 3. D. 5 và 4.
Lời giải:
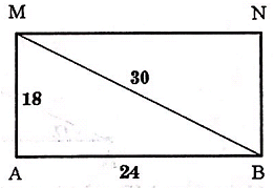
Chọn B.
* Số điểm cực đại trên đoạn MN được xác định như sau:
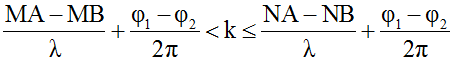
Trong đó: bước sóng λ = v/f = 120/20 = 6cm; φ1 = 0; φ2 = π/3
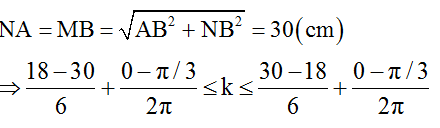
↔ -2,17 ≤ k ≤ 1,83 → có 4 giá trị nguyên ứng với 4 điểm cực đại trên MN.
* Số điểm cực tiểu trên đoạn MN được xác định như sau:
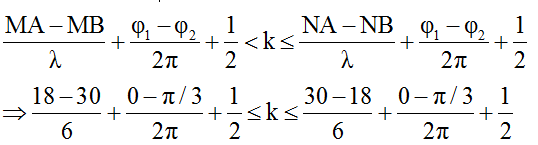
↔ -1,67 ≤ k ≤ 2,33 → có 4 giá trị nguyên ứng với 4 điểm cực tiểu trên MN.
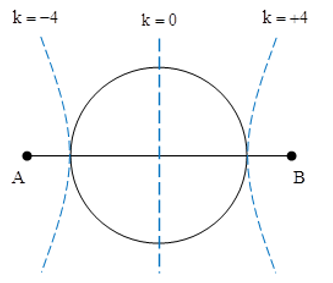
Câu 10: Trên mặt nước có hai nguồn kết hợp đặt ở A và B cách nhau 68 mm, dao động điều hòa cùng tần số, cùng pha theo phương vuông góc với mặt nước. Trên đoạn AB, hai phần tử nước dao động với biên độ cực đại có vị trí cân bằng cách nhau một đoạn ngắn nhất là 5 mm. Điểm C là trung điểm của AB. Trên đường tròn tâm C bán kính 20 mm nằm trên mặt nước có bao nhiêu điểm dao động với biên độ cực đại ?
A. 20 B. 18 C. 16 D. 14
Lời giải:
Chọn C.
Hai nguồn đồng pha nên đường trung trực của AB là cực đại bậc 0.
Khoảng cách giữa hai điểm gần nhau nhất trên đoạn AB dao động cực đại cách nhau 5mm
λ/2 = 5 => λ = 10mm .
Xét tỉ số R/0,5λ = 20/5 = 4 đoạn có độ dài λ/2
Từ hình vẽ ta thấy có hai đường cực đại (k = -4 và k = 4) tiếp xúc với đường tròn và 7 đường cắt đường tròn tại 2 điểm nên số cực đại trên đường tròn là: N = 7.2 + 2 = 16 điểm.
Câu 11: Trên mặt nước có hai nguồn kết hợp S1 và S2 cách nhau 10 cm có phương trình lần lượt là u1 = 3cos(40πt + π/6), u2 = 4cos(40πt + 2π/3). Biết tốc độ truyền sóng là 40cm/s. Số điểm dao động với biên độ 7cm (cực đại) trên đường tròn trung điểm I của S1S2, bán kính 4cm là bao nhiêu?
A. 32. B. 16. C. 38. D. 40.
Lời giải:
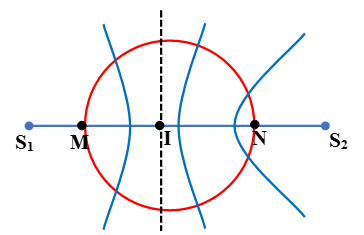
Chọn B.
Số điểm dao động cực đại trên MN (đường kính của đường tròn) được xác định như sau:
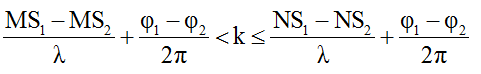
Trong đó:
λ = v/f = 40/20 = 2cm; φ1 = π/6, φ2 = 2π/3.
MS1 = IS1 – MI = 5 – 4 = 1cm.
MS2 = S1S2 – MS1 = 10 – 1 = 9cm.
NS2 = IS2 – IN = 5 – 4 = 1cm.
NS1 = S1S2 – NS2 = 10 – 1 = 9cm.
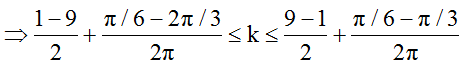
=> -4,25 ≤ k ≤ 3,75
Vì k ∈ Z nên k = -4;...; -1; 0; 1; 2 ;3. Do đó có 8 điểm cực đại giao thoa trên MN tương ứng với 8 đường hyperbol cực đại cắt đường tròn tại 16 điểm.
Câu 12: Hai nguồn sóng kết hợp giống hệt nhau được đặt cách nhau một khoảng cách x trên đường kính của một vòng tròn bán kính R (x < R) và đối xứng qua tâm của vòng tròn. Biết rằng mỗi nguồn đều phát sóng có bước sóng λ và x = 6λ. Số điểm dao động cực đại trên vòng tròn là
A. 26 B. 24 C. 22. D. 20.
Lời giải:
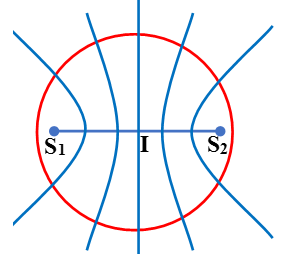
Chọn B.
Vì S1S2 = x < R nên đường tròn tâm I luôn cắt tất cả các đường cực đại tại hai điểm.
Hai nguồn sóng kết hợp giống hệt nhau nên số điểm cực đại trên S1S2 được xác định như sau:
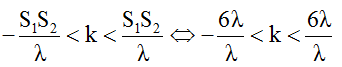
↔ -6 < k < 6.
Vì k ∈ Z nên k = -6;...; -1; 0; 1; 2;... ;6.
Do đó có 13 điểm cực đại giao thoa trên S1S2 tương ứng với 13 đường hyperbol cực đại cắt đường tròn tại 26 điểm.
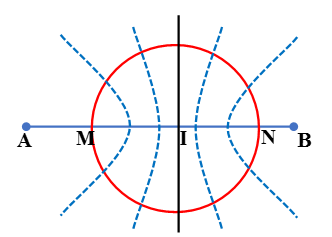
Câu 13: Trên bề mặt chất lỏng cho hai nguồn dao động vuông góc với bề mặt chất lỏng có phương trình dao động uA = 3cos10πt cm và uB = 5cos(10πt + π/3) cm. Tốc độ truyền sóng trên dây là v = 50 cm/s. AB = 30 cm. Cho điểm C trên đoạn AB, cách A khoảng 18 cm và cách B 12 cm. Vẽ vòng tròn đường kính 10 cm, tâm tại C. Số điểm dao động cực tiểu trên đường tròn là:
A. 7 B. 6 C. 8 D. 4
Lời giải:
Chọn D.
Số điểm dao động cực tiểu trên MN (đường kính của đường tròn) được xác định như sau:
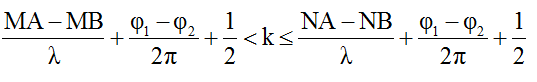
Trong đó:
Bước sóng λ = v/f = 50/5 = 10cm; φ1 = 0, φ2 = π/3.
MA = CA – MC = 18 – 5 = 13cm.
MB = 30 – 13 = 17cm.
NB = CB – CN = 12 – 5 = 7cm.
NB = 30 – 7 = 23cm.
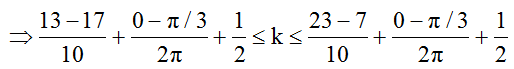
=> -0,07 ≤ k ≤ 1,93
Vì k ∈ Z nên k = 0; 1. Do đó có 2 điểm cực tiểu giao thoa trên MN tương ứng với hai đường hyperbol cực tiểu cắt đường tròn tại 4 điểm.
Câu 14: Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn AB cách nhau 14,5 cm dao động ngược pha. Điểm M trên AB gần trung điểm O của AB nhất, cách O một đoạn 0,5 cm luôn dao động cực đại. Số điểm dao động cực đại trên đường elíp thuộc mặt nước nhận A, B làm tiêu điểm là :
A. 26 B. 28 C. 18 D. 14
Lời giải:
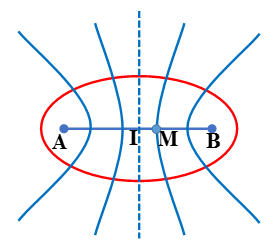
Chọn B.
Hai nguồn ngược pha nên đường trung trực của AB là đường cực tiểu, do vậy MI = λ/4
Suy ra λ = 2cm.
Số điểm dao động cực tiểu trên AB được xác định như sau:
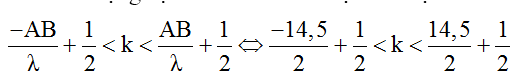
↔ -6,75 < k < 7,75
Vì k ∈ Z nên k = -6...; -1; 0; 1; 2;... ;7.
Do đó có 14 điểm cực đại giao thoa trên S1S2 tương ứng với 14 đường hyperbol cực đại cắt đường elip tại 28 điểm.
Câu 15: Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 24 cm, dao động theo phương thẳng đứng với phương trình là uA = uB = acos60πt (với t tính bằng s). Tốc độ truyền sóng của mặt chất lỏng là v = 45 cm/s. Gọi MN = 4 cm là đoạn thẳng trên mặt chất lỏng có chung trung trực với AB. Khoảng cách xa nhất giữa MN với AB là bao nhiêu để có ít nhất 5 điểm dao động cực đại nằm trên MN?
A. 12,7 cm B. 10,5 cm C. 14,2 cm D. 6,4 cm
Lời giải:
Chọn B.
Bước sóng: λ = v/f = 45/30 = 1,5cm.
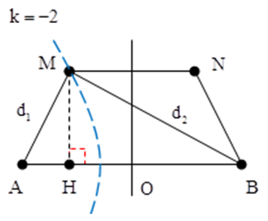
Vì MN có chung đường trung trực với AB nên MN tạo với AB một hình thang cân.
Số điểm dao động với biên độ cực đại trên AB được xác định như sau:
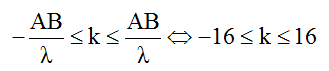
Để có ít nhất 5 điểm dao động cực đại nằm trên MN thì M phải nằm trên cực đại ứng với k = -2.
Khi đó: d2M– d1M = 2λ = 3cm.
Mặt khác:
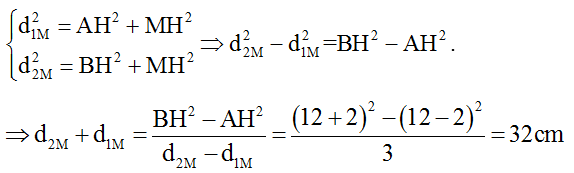
Ta tính được d1M = 14,5cm, từ đó suy ra
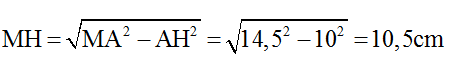
Khoảng cách xa nhất giữa MN với AB là 10,5cm.
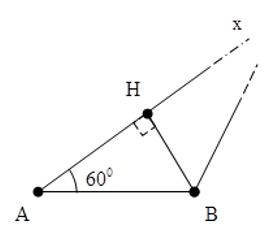
Câu 16: Cho hai nguồn AB dao động cùng pha trên mặt nước cách nhau 5 lần bước sóng. Ax là tia thuộc mặt nước hợp với AB góc 60o. Trên Ax có số điểm dao động với biên độ cực đại là (không tính phần tử tại A)
A. 7 B. 8 C. 9 D. 10
Lời giải:
Chọn A.
Số điểm dao động với biên độ cực đại trên AB được xác định như sau:
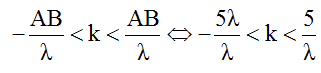
⇔ - 5 < k < 5
Gọi H là hình chiếu của B lên Ax, xét điểm M nằm trên Ax khi M ở vô cùng ta có:
Xét tỉ số
Như vậy Ax cắt hypebol cực đại ứng với k = 2.
Vậy số điểm dao động với biên độ cực đại trên Ax sẽ là 7 tương ứng với k = -4; -3; -2; -1; 0; 0; 1; 2.
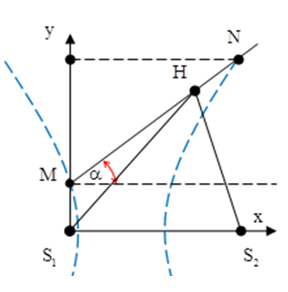
Câu 17: Trong thí nghiệm giao thoa sóng nước, hai nguồn sóng S1 và S2 cách nhau 11 cm dao động theo phương vuông góc với mặt nước với cùng phương trình u1 = u2 = 5cos(100πt) mm. Tốc độ truyền sóng v = 0,5m/s và biên độ sóng không đổi trong quá trình truyền đi. Chọn hệ trục xOy thuộc mặt phẳng mặt nước khi yên lặng, gốc O trùng với S1, Ox trùng với S1S2. Trong không gian, phía trên mặt nước có một chất điểm chuyển động mà hình chiếu P của nó tới mặt nước chuyển động với phương trình quỹ đạo y = x + 2 và có tốc độ v1 = 5√2 cm/s. Trong thời gian t = 2s kể từ lúc P có tọa độ xP = 0 thì P cắt bao nhiêu vân cực đại trong vùng giao thoa sóng?
A. 13 B. 14 C. 22 D. 15.
Lời giải:
Chọn A.
Bước sóng của sóng λ = v.T = 1cm.
Quãng đường mà P đi được trong khoảng thời gian 2 s:
S = MN = v1.t = 5√2.2 = 10√2 cm.
Hệ số góc của đường MN là: tanα = 1 → α = 45o.
Suy ra tọa độ của điểm N:
xN = MNcos45o = 10cm; yN = 2 + MN.sin45o = 12cm.
Gọi H là một điểm bất kì nằm trên đường thẳng y = x + 2.
Dễ thấy rằng để H là một cực đại thì d1H – d2H = k.λ.
Với khoảng giá trị của d1H – d2H là: MS1 – MS2 ≤ d1H – d2H ≤ NS1 – NS2.
Từ hình vẽ ta có:
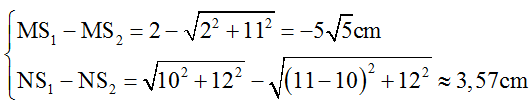
Ta thu được -9,1 ≤ d1H – d2H = k.λ ≤ 3,58 ↔ -9,1 ≤ k ≤ 3,58.
Vậy có 13 giá trị k nguyên ứng với 13 điểm cực đại trên MN → P cắt 13 vân cực đại trong vùng giao thoa sóng.