Cách tìm thời gian ngắn nhất, lớn nhất vật đi qua li độ, vật có vận tốc, gia tốc hay, chi tiết - Vật Lí lớp 12

Cách tìm thời gian ngắn nhất, lớn nhất vật đi qua li độ, vật có vận tốc, gia tốc hay, chi tiết

Với Cách tìm thời gian ngắn nhất, lớn nhất vật đi qua li độ, vật có vận tốc, gia tốc hay, chi tiết Vật Lí lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm thời gian ngắn nhất, lớn nhất vật đi qua li độ, vật có vận tốc, gia tốc từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

A. Phương pháp & Ví dụ

a) Bài toán tính khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ x₁ đến x₂

Phương pháp 1: Phương pháp đường tròn lượng giác (khi x có giá trị đặc biệt)

Ta dùng mối liên hệ giữa DĐĐH và CĐTĐ đều để tính. Khi vật dao động điều hoà từ x₁ đến x₂ thì tương ứng với vật chuyển động tròn đều từ M đến N (chú ý x₁ và x₂ là hình chiếu vuông góc của M và N lên trục Ox.

Thời gian ngắn nhất vật dao động đi từ x₁ đến x₂ bằng thời gian vật chuyển động tròn đều từ M đến N

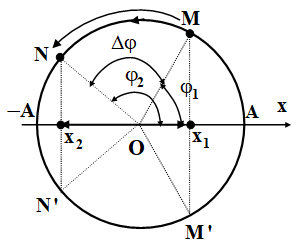
Ta vận dụng:

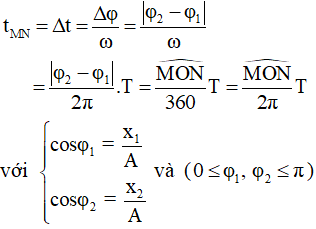
Ta làm theo các bước sau:

* Bước 1: Vẽ đường tròn có bán kính R = A (biên độ) và trục Ox nằm ngang

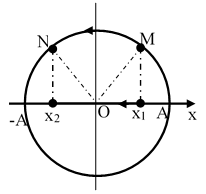
* Bước 2 :

– Xác định vị trí vật lúc t = 0 thì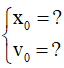

– Xác định vị trí vật lúc t (x_t đã biết)

* Bước 3 : Xác định góc quét Δφ = ?

* Bước 4 :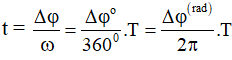

Phương pháp 2:

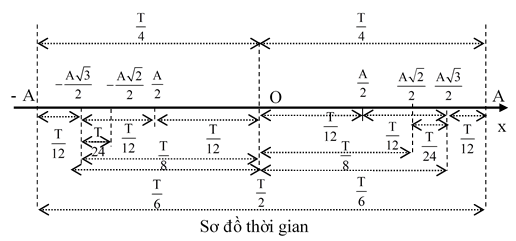
Ngoài ra, nếu vị trí x* là những vị trí đặc biệt, ví dụ như 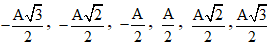… thì ta phải ghi nhớ bảng phân bố thời gian và những thời gian đặc biệt nó sẽ giúp chúng ta giải bài toán trắc nghiệm rất nhanh chóng và chính xác.

Các khoảng thời gian ngắn nhất đặc biệt:

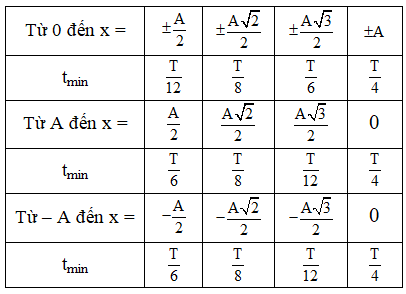
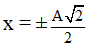
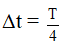
Vật 2 lần liên tiếp đi qua thì .

Ví dụ 1: Một chất điểm dao động điều hòa với phương trình x = Acos(ωt + φ) và có chu kỳ T. Tính khoảng thời gian ngắn nhất mà vật đi từ vị trí biên có li độ x = -A/2 đến vị trí ?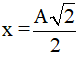

Hướng dẫn:

Cách 1: Sử dụng mối liên hệ giữa đường tròn lượng giác và dao động điều hòa.

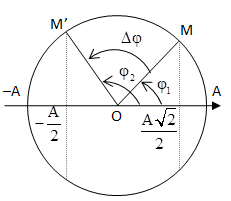
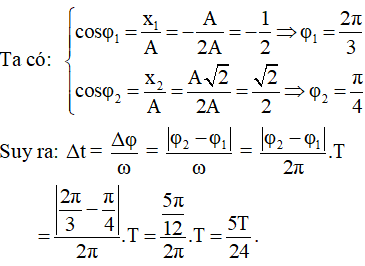
Chọn đáp án D

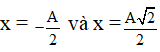
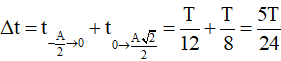
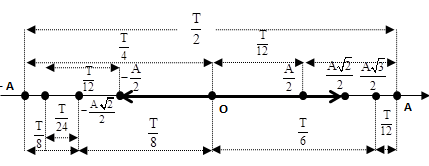
Cách 2: Ta nhận thấy vị trí là những vị trí đặc biệt nên:

Chọn đáp án D

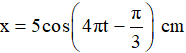
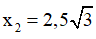
Ví dụ 2: Một vật dao động trên trục ox với phương trình . Khoảng thời gian ngắn nhất để vật đi từ li độ x₁ = -2,5 cm đến li độ ?

Hướng dẫn:

Cách 1: Sử dụng mối liên hệ giữa dao động điều hòa và chuyển động tròn đều.

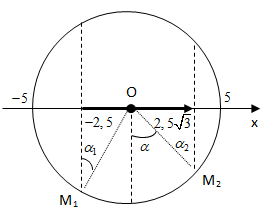
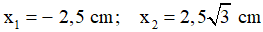
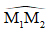
Vẽ đường tròn tâm O, bán kính R = A = 5 cm, kẻ trục Ox nằm ngang và đánh dấu vị trí các điểm . Xác định cung tương ứng như hình vẽ.

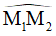
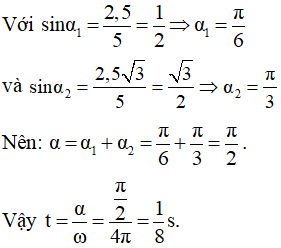
Ta cần tìm góc α ở tâm do cung chắn. Trong trường hợp này, góc α có thể tính α = α₁ + α₂.

Chọn đáp án A

Cách 2: Nhớ các trường hợp đặc biệt (xem sơ đồ phân bố thời gian)

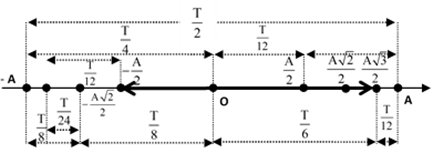
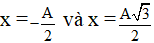
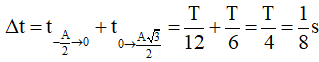
Ta nhận thấy vị trí là những vị trí đặc biệt nên:

Chọn đáp án D

Ví dụ 3: Một chất điểm dao động điều hòa với chu kì T với tốc độ cực đại v_Max. Thời gian ngắn nhất vật đi từ điểm mà tốc độ của vật bằng 0 đến điểm mà tốc độ của vật bằng 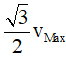là :

A. T/8    B. T/16    C.T/6    D. T/12

Hướng dẫn:

Cách 1

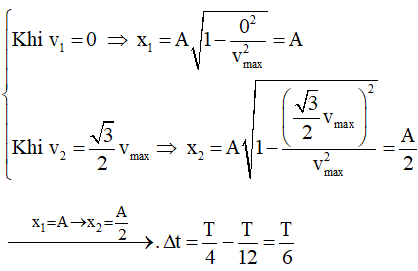
Chọn đáp án C

Nhận xét: Đây là cách giải rất hay, cho kết quả rất nhanh, chúng ta cần hiểu rỏ sơ đồ phân bố thời gian, vận tốc, gia tốc để giải nhanh những bài toán này.

Cách 2: Sử dụng vòng tròn lượng giác biểu diễn vận tốc.

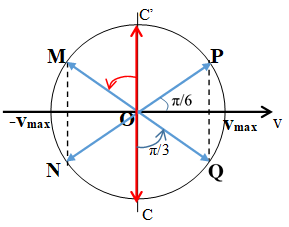
Thời gian ngắn nhất vật đi từ điểm mà tốc độ của vật bằng 0 đến điểm mà tốc độ của vật bằng 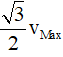là ứng với cung CQ hoặc cung C’M.

Từ hình học ta thấy 2 cung này có số đo π/3 ứng với thời gian T/6

b) Dạng bài toán cho quãng đường S < 2A, tìm khoảng thời gian nhỏ nhất và lớn nhất

Vật có v_max khi qua VTCB, v_min khi qua vị trí biên nên trong cùng một quãng đường, khoảng thời gian sẽ dài khi vật ở gần vị trí biên, khoảng thời gian sẽ ngắn khi đi xung quanh gần VTCB.

Vẽ quãng đường bài toán cho ở các vị trí có v_max, v_min. Từ quãng đường suy ra các vị trí đầu x₁ và vị trí cuối x₂. Sau đó sử dụng cách giải như dạng toán tìm quảng đường lớn nhất, nhỏ nhất trong cùng một khoảng thời gian.

Ví dụ 1: Một vật dao động điều hoà trên trục Ox theo phương trình 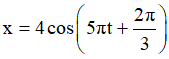cm. Tính thời gian dài nhất và ngắn nhất mà vật đi được quãng đường bằng nhau và bằng 4√2 cm.

Hướng dẫn:

Đây là dạng bài toán ngược lại so với bài toán trên cho trường hợp S < 2A.

Vật có vận tốc lớn nhất khi qua VTCB, nhỏ nhất khi qua vị trí biên nên trong cùng một khoảng thời gian quãng đường đi được càng lớn khi vật ở càng gần VTCB và càng nhỏ khi càng gần vị trí biên. Và từ các công thức tính:

+ Quãng đường lớn nhất 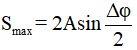(1)

+ Quãng đường nhỏ nhất 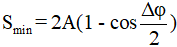(2)

Ta thay Δφ = ωΔt, S_max = S_min = S = A (Δt tương ứng là t_max và t_min ứng với S_max và S_min) vào (1) và (2) ta được:

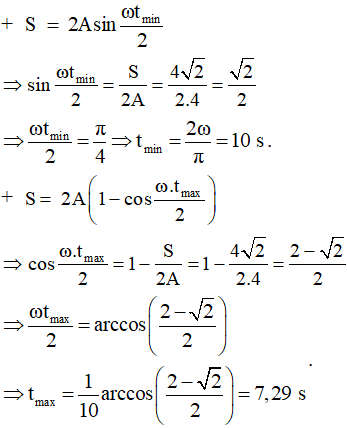
Chú ý:

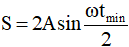
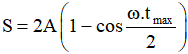
+ Nếu gặp dạng bài toán này với S < 2A, ta có thể áp dụng ngay công thức dưới đây: và

+ Từ dạng bài toán này, chúng ta cũng có thể mở rộng cho bài toàn tính tần số góc ω, tần số f hoặc chu kì T.

c) Tìm thời gian trong một chu kì T để vật dao động có giá trị {x, v, a, F} lớn hơn hay nhỏ hơn giá trị {x₀, v₀, a₀, F₀} nào đó.

Ví dụ 1: Vật m dao động điều hòa có phương trình x = Acos(ωt + φ) với chu kì dao động là T. Gọi gia tốc a₀ có giá trị nào đó (với a₀ < a_max).

Hướng dẫn:

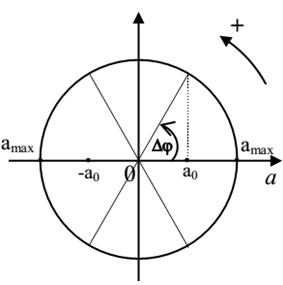
Đặt 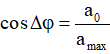(với 0 < Δφ < π) khi đó:

* Gọi Δt là thời gian trong một chu kì để gia tốc a có độ lớn lớn hơn giá trị a₀.

Thì: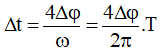

* Gọi Δt là thời gian trong một chu kì để gia tốc a có độ lớn nhỏ hơn giá trị a₀.

Thì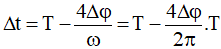

* Gọi Δt là thời gian trong một chu kì để gia tốc a có giá trị đại số lớn hơn giá trị a₀.

Thì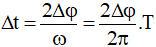

* Gọi Δt là thời gian trong một chu kì để gia tốc a có giá trị đại số nhỏ hơn giá trị a₀.

Thì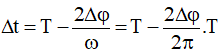

Vậy: Sẽ làm tương tự nếu bài toán yêu cầu tìm thời gian trong một chu kì T để vật dao động có giá trị {x, v, F} lớn hơn hay nhỏ hơn giá trị {x₀, v₀, F₀} nào đó.

B. Bài tập trắc nghiệm

Câu 1. Vật dao động điều hòa có phương trình: x = Acosωt. Thời gian ngắn nhất kể từ lúc bắt đầu dao động đến lúc vật có li độ x = -A/2 là:

A. T/6 s    B. T/8 s    C. T/3 s    D. T/4s

Lời giải:

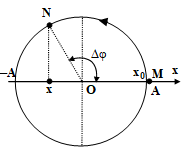
Tại t = 0: x₀ = A, v₀ = 0: Trên đường tròn ứng với vị trí M.

Tại t: x = -A/2. Trên đường tròn ứng với vị trí N.

Vật đi ngược chiều (+) quay được góc Δφ = 120º = 2π/3 rad.

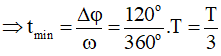
Chọn đáp án C

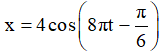
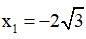
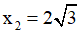
Câu 2. Vật dao động điều hòa theo phương trình: . Thời gian ngắn nhất vật đi từ cm theo chiều dương đến vị trí có li độ cm theo chiều dương là:

A. 1/16s    B. 1/12s    C. 1/10s    D. 1/20 s

Lời giải:

Vật dao động điều hòa từ x₁ đến x₂ theo chiều dương tương ứng vật CĐTĐ từ M đến N.

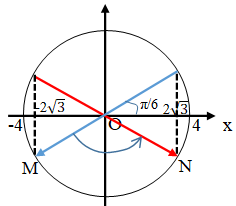
Trong thời gian t vật quay được góc Δφ = 120º = 2π/3 rad

Vậy: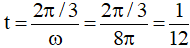

Chọn đáp án B

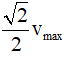
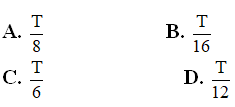
Câu 3. Một chất điểm dao động điều hòa với chu kì T với tốc độ cực đại v_max. Thời gian ngắn nhất vật đi từ điểm mà tốc độ của vật bằng 0 đến điểm mà tốc độ của vật bằng là:

Lời giải:

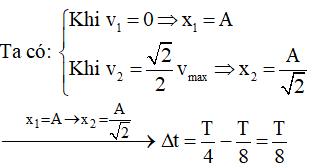
Chọn đáp án A

Câu 4. Một chất điểm dao động điều hòa với chu kì T với tốc độ cực đại là v_max. Thời gian ngắn nhất vật đi từ điểm mà tốc độ của vật bằng 0,5v_max đến điểm mà tốc độ của vật bằng 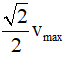là:

A. T/24    B. T/16    C. T/6    D. T/12

Lời giải:

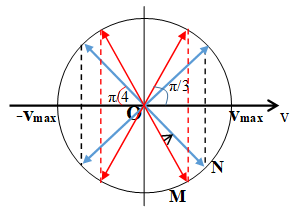
Sử dụng vòng tròn lượng giác biểu diễn vận tốc

Thời gian ngắn nhất vật đi từ điểm mà tốc độ của vật bằng 0,5v_max đến điểm mà tốc độ của vật bằng 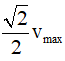là ứng với cung MN.

Từ hình học ta thấy 2 cung này có số đo π/3 - π/4 = π/12 ứng với thời gian T/24.

Chọn đáp án A

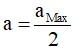
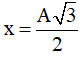
Câu 5. Một chất điểm dao động điều hòa với chu kì T với tốc độ cực đại là a_max. Thời gian ngắn nhất vật đi từ điểm mà vật có gia tốc đến điểm mà vật có li độ là :

A. T/8    B. T/4    C. T/6    D. T/2

Lời giải:

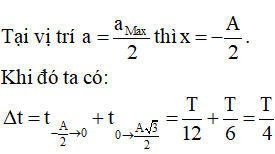
Chọn đáp án B

Câu 6. Một vật dao động điều hoà trên trục Ox. Gọi t_max và t_min là thời gian dài nhất và ngắn nhất mà vật đi được quãng đường bằng biên độ. Tỉ số 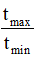là

A. 1/2    B. 2    C. 1/12    D. 1/3

Lời giải:

Cùng một quãng đường A, vật đi thời gian ngắn nhất (t_min) là xung quanh gốc tọa độ và đi hết thời gian dài nhất (t_max) là quanh biên.

Thời gian ngắn nhất:

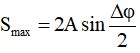
suy ra:

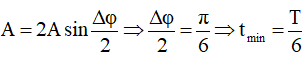
Thời gian dài nhất:

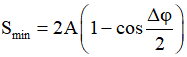
suy ra:

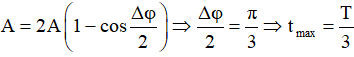
Suy ra: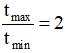

Chọn đáp án B

Câu 7. Một vật dao động điều hoà trên trục Ox theo phương trình 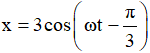cm. So sánh những quãng đường bằng nhau và bằng 3√3 cm thì khoảng thời gian dài nhất là ¾ s. Hãy tìm tần số f của dao động?

A. 35Hz.    B. 45Hz.    C. 10Hz.    D. 20Hz

Lời giải:

Theo bài toán trên, từ công thức:

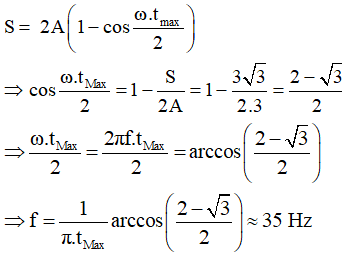
Chọn A

Câu 8. Vật đang dao động điều hòa dọc theo đường thẳng. Một điểm M nằm cố định trên đường thẳng đó, phía ngoài khoảng chuyển động của vật, tại thời điểm t thì vật xa điểm M nhất, sau đó một khoảng thời gian ngắn nhất ∆t thì vật gần điểm M nhất. Độ lớn vận tốc của vật sẽ bằng nữa vận tốc cực đại vào thời điểm gần nhất là :

A. t + ∆t/3.    B. t + ∆t/6.

C. t + ∆t/4.    D. 0,5t + 0,25∆t

Lời giải:

Thời gian ngắn nhất vật đi từ điểm M xa nhất đến điểm M gần nhất là nữa chu kỳ nên ∆t = T/2 → T = 2.∆t.

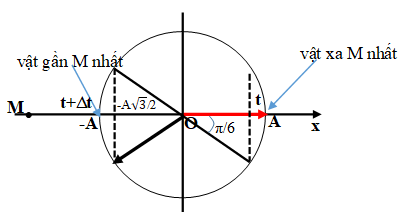
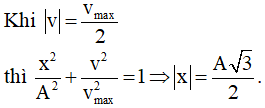
Thời gian ngắn nhất vật đi từ x = A đến 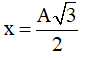là T/12

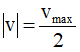
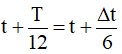
Thời điểm gần nhất vật có là:

Câu 9. Một chất điểm đang dao động điều hòa trên một đoạn thẳng. Trên đoạn thẳng đó có 7 điểm theo đúng thứ tự M₁, M₂, M₃, M₄, M₅, M₆ và M₇ với M₄ là vị trí cân bằng. Biết cứ 0,05 s thì chất điểm lại đi qua các điểm M₁, M₂, M₃, M₄, M₅, M₆ và M₇ (tốc độ dài M₁ và M₇ bằng 0). Tốc độ của nó lúc đi qua điểm M₃ là 20π cm/s. Biên độ A bằng

A. 4cm.    B. 6cm.    C. 12cm.    D. 4√3 cm

Lời giải:

Vì tốc độ dài M₁ và M₇ bằng 0 nên M₁ và M₇ là hai biên của quỹ đạo.

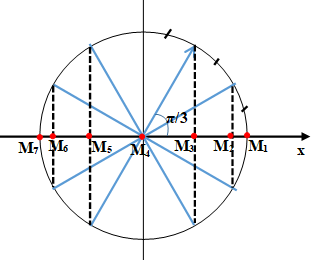
Dựa vào vòng tròn lượng giác ta được:

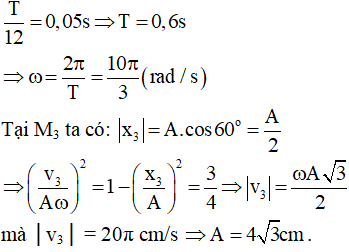
Chọn D

Câu 10. Một chất điểm dao động điều hòa với chu kì T. Khoảng thời gian trong một chu kì để vật có độ lớn gia tốc lớn hơn một nửa gia tốc cực đại là

A. T/3    B. 2T/3    C. T/6    D. T/2

Lời giải:

Gọi Δt là thời gian trong một chu kì để gia tốc a có độ lớn lớn hơn giá trị a₀ = a_max/2.

Từ vòng tròn lượng giác biểu diễn gia tốc a ta tìm được: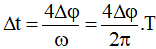

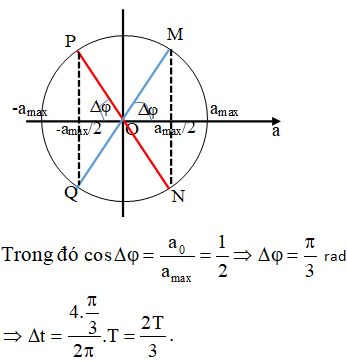
Chọn đáp án B

Câu 11. Một chất điểm dao động điều hòa với chu kì T. Khoảng thời gian trong một chu kì để vật có vận tốc không nhỏ hơn một nửa tốc độ cực đại là:

Lời giải:

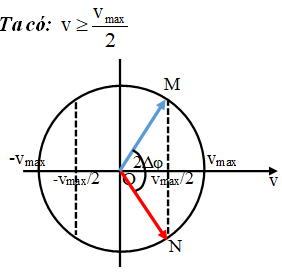
Gọi Δt là thời gian trong một chu kì để vận tốc v không nhỏ hơn giá trị v₀ = v_max/2.

Từ vòng tròn lượng giác biểu diễn vận tốc v ta tìm được: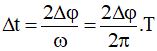

Trong đó

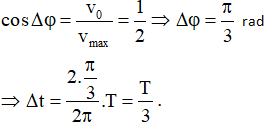
Chọn đáp án A

Câu 12. Một con lắc lò xo dao động điều hòa với chu kỳ T, biên độ 5cm. Biết trong một chu kỳ, khoảng thời gian để vật nhỏ của con lắc có độ lớn gia tốc không vượt quá 100cm/s² là T/3. Lấy π² = 10. Tần số dao động của vật là:

A. 4Hz.    B. 3Hz.    C. 2Hz    D. 1Hz.

Lời giải:

Ta có:

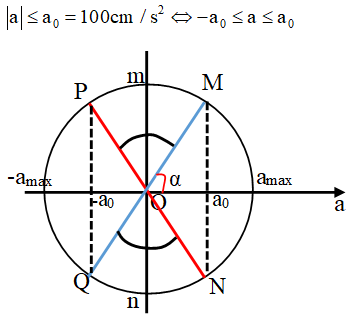
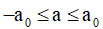
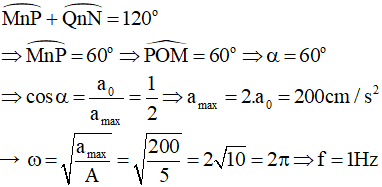
Từ vòng tròn lượng giác biểu diễn gia tốc a ta tìm được vùng mà thỏa mãn điều kiện là ứng với hai cung . Vì khoảng thời gian thỏa mãn điều kiện của gia tốc là T/3 nên:

Chọn D.

Câu 13. Một chất điểm dao động điều hòa với chu kì T. Gọi vtb là tốc độ trung bình của chất điểm trong một chu kì, v là tốc độ tức thời của chất điểm. Trong một chu kì, khoảng thời gian mà 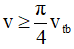là:

A. T/6    B. 2T/3    C.T/3    D. T/2

Lời giải:

Tốc độ trung bình trong một chu kì là: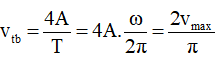

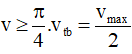
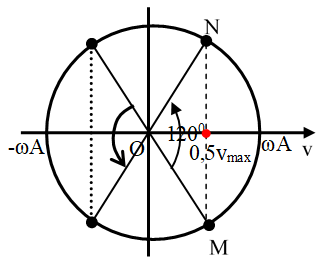
Mà (chú ý ở đây v là tốc độ). Do đó trên vòng tròn biểu diễn vận tốc có hai cung thỏa mãn được đánh dấu như hình vẽ.

Từ hình học ta tìm được khoảng thời gian trong một chu kì mà tốc độ v thỏa mãn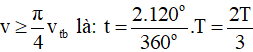

Chọn đáp án B

Câu 14. Một vật dao động điều hòa với tần số 2 Hz. Tính thời gian trong một chu kì W_t ≤ 2W_đ.

A. 0,196 s.    B. 0,146 s.

C. 0,096 s.    D. 0,304 s.

Lời giải:

Ta quy về li độ:

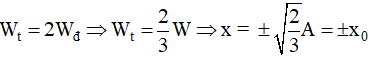
Như vậy vùng thỏa mãn W_t ≤ 2W_đ nằm trong đoạn [-x₀; x₀].

Trên vòng tròn lượng giác biểu diễn li độ có hai cung thoản mãn M₁mM₂ và cung M₃nM₄

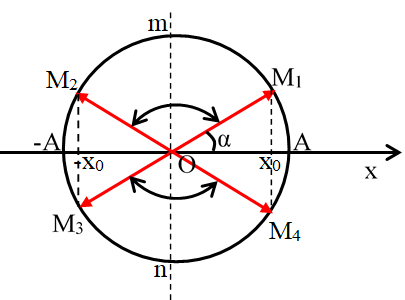
Ta có:

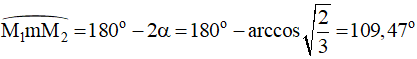
Suy ra khoảng thời gian trong một chu kì mà W_t ≤ 2W_đ là:

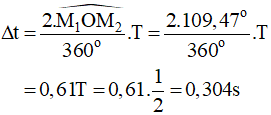
Chọn D.

Câu 15. Vật dao động điều hòa có vận tốc cực đại bằng 3 m/s và gia tốc cực đại bằng 30π (m/s²). Thời điểm ban đầu vật có vận tốc −1,5 m/s và thế năng đang giảm. Hỏi sau thời gian ngắn nhất là bao nhiêu vật có gia tốc bằng -15π (m/s²)?

A. 1/10 s.    B. 1/60 s.    C. 1/30 s.    D. 1/120 s.

Lời giải:

Ta có: v_max = ωA; a_max = ω²A → ω = a_max/v_max = 10π (rad/s);

Thời điểm ban đầu vật có vận tốc v₁ = −1,5 m/s = -v_max /2

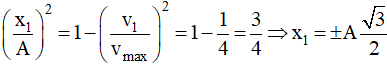
Vì lúc này thế năng đang giảm và v₁ < 0 nên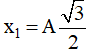

Khi a = a₂ = -15π (m/s²) = -a_max /2 nên x₂ = A/2

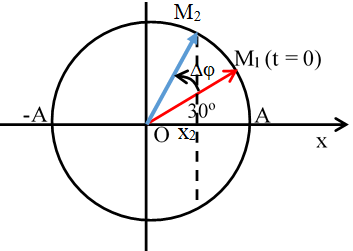
Sử dụng vòng tròn lượng giác biểu diễn li độ ta tìm được thời điểm nhỏ nhất mà vật có gia tốc bằng -15π (m/s²) ứng với điểm M₂ với góc quét:

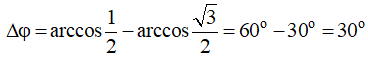
Vậy thời gian nhỏ nhất cần tìm là:

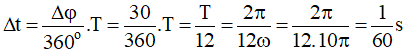
Chọn B.