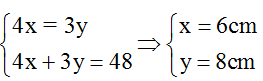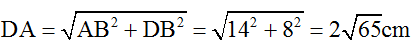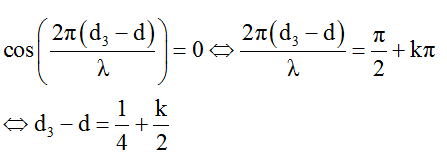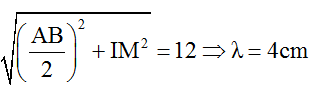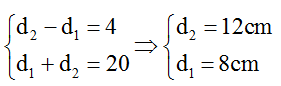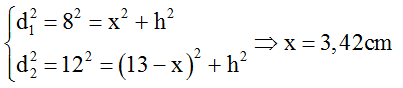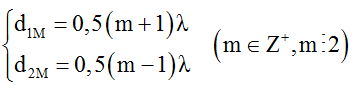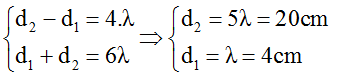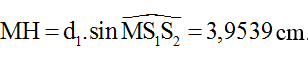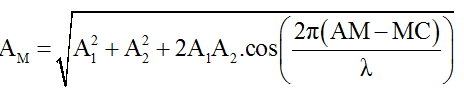Bài tập giao thoa sóng cơ nâng cao, hay và khó, có lời giải - Vật Lí lớp 12

---

Bài tập giao thoa sóng cơ nâng cao, hay và khó, có lời giải

Với Bài tập giao thoa sóng cơ nâng cao, hay và khó, có lời giải Vật Lí lớp 12 tổng hợp 15 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giao thoa sóng cơ nâng cao, hay và khó từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

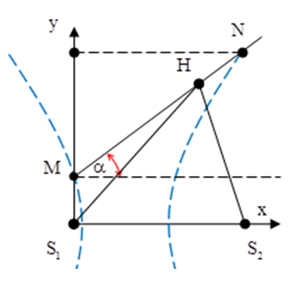
Câu 1: Trong thí nghiệm giao thoa sóng nước, hai nguồn sóng S₁ và S₂ cách nhau 11 cm dao động theo phương vuông góc với mặt nước với cùng phương trình u₁ = u₂ = 5cos(100πt) mm. Tốc độ truyền sóng v = 0,5m/s và biên độ sóng không đổi trong quá trình truyền đi. Chọn hệ trục xOy thuộc mặt phẳng mặt nước khi yên lặng, gốc O trùng với S₁, Ox trùng với S₁S₂. Trong không gian, phía trên mặt nước có một chất điểm chuyển động mà hình chiếu P của nó tới mặt nước chuyển động với phương trình quỹ đạo y = x + 2 và có tốc độ v₁ = 5√2 cm/s. Trong thời gian t = 2s kể từ lúc P có tọa độ x_P = 0 thì P cắt bao nhiêu vân cực đại trong vùng giao thoa sóng?

A. 13    B. 14    C. 22    D. 15.

Lời giải:

Chọn A.

Bước sóng của sóng λ = v.T = 1cm.

Quãng đường mà P đi được trong khoảng thời gian 2s:

S = MN = v1.t = 5√2.2 = 10√2 cm.

Hệ số góc của đường MN là: tanα = 1 → α = 45^o.

Suy ra tọa độ của điểm N:

x_N = MNcos45^o = 10cm; y_N = 2 + MN.sin45^o = 12cm.

Gọi H là một điểm bất kì nằm trên đường thẳng y = x + 2.

Dễ thấy rằng để H là một cực đại thì d_1H – d_2H = k.λ.

Với khoảng giá trị của d_1H – d_2H là: MS₁ – MS₂ ≤ d_1H – d_2H ≤ NS₁ – NS₂.

Từ hình vẽ ta có:

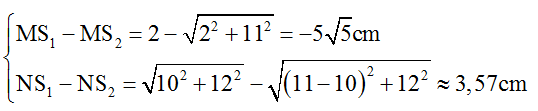
Ta thu được -9,1 ≤ d_1H – d_2H = k.λ ≤ 3,58 ↔ -9,1 ≤ k ≤ 3,58.

Vậy có 13 giá trị k nguyên ứng với 13 điểm cực đại trên MN → P cắt 13 vân cực đại trong vùng giao thoa sóng.

Câu 2: Trên mặt nước, hai nguồn kết hợp được đặt ở A và B cách nhau 14 cm, dao động điều hòa cùng tần số, cùng pha, theo phương vuông góc với mặt nước. Sóng truyền trên mặt nước với bước sóng 0,9 cm. Điểm M nằm trên đoạn AB cách A một đoạn 6 cm. Ax, By là hai nửa đường thẳng trên mặt nước, cùng một phía so với AB và vuông góc với AB. Cho điểm C di chuyển trên Ax và điểm D di chuyển trên By sao cho MC luôn vuông góc với MD. Khi diện tích của ∆MCD có giá trị nhỏ nhất thì số điểm dao động với biên độ cực đại trên MD là:

A. 12.    B. 13.    C. 8.    D. 6.

Lời giải:

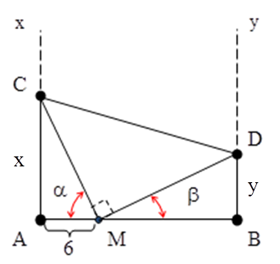
Chọn A.

+ Diện tích tam giác MCD:

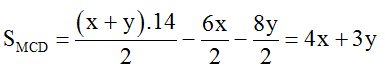
Mặc khác vì α + β = 90^o nên tanα = x/6 = 8/y => xy = 48

⇔ 4x.3y = 576 = const

Áp dụng bất đẳng thức Cosi, ta có :

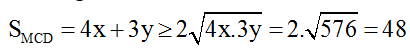
Dấu bằng xảy ra khi:

Khi đó:

Số cực đại trên MD được xác định như sau:

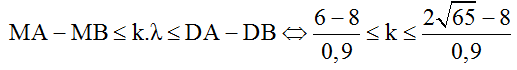
↔ -2,2 ≤ k ≤ 9,02.

Suy ra có 12 giá trị k ϵ Z ứng với 12 điểm cực đại trên đoạn MD.

Câu 3: Trên mặt chất lỏng có hai nguồn sóng cùng tần số, cùng pha đặt tại hai điểm A và B. Cho bước sóng do các nguồn gây ra là λ = 5 cm. Trên nửa đường thẳng đi qua B trên mặt chất lỏng, hai điểm M và N (N gần B hơn), điểm M dao động với biên độ cực đại, N dao động với biên độ cực tiểu, giữa M và N có ba điểm dao động với biên độ cực đại khác. Biết hiệu MA – NA = 1,2 cm. Nếu đặt hai nguồn sóng này tại M và N thì số điểm dao động với biên độ cực đại trên đoạn thẳng AB là

A. 3.    B. 4.    C. 1.    D. 2.

Lời giải:

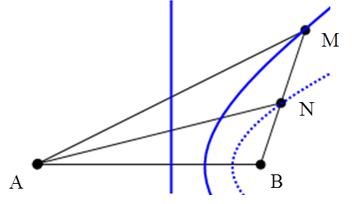
Chọn A.

+ M thuộc cực đại và N thuộc cực tiểu nên ta có :

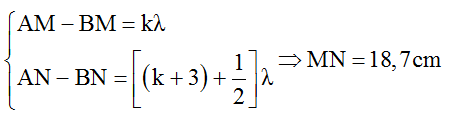
Với nguồn đặt tại M, N. Xét đoạn AB, ta có:

MA - NA ≤ kλ ≤ MB - NB ⇔ 0,24 ≤ kλ ≤ 3,74

Vậy có 3 cực đại.

Câu 4: Trên mặt nước trong một chậu rất rộng có hai nguồn phát sóng nước đồng bộ S₁, S₂ (cùng phương, cùng tần số, cùng biên độ và pha ban đầu) dao động điều hòa với tần số f = 50Hz, khoảng cách giữa hai nguồn S₁S₂ = 2d. Người ta đặt một đĩa nhựa tròn bán kính r = 1,2cm (r < d) lên đáy nằm ngang của chậu sao cho S₂ nằm trên trục đi qua tâm và vuông góc với mặt đĩa; bề dày đĩa nhỏ hơn chiều cao nước trong chậu. Tốc độ truyền sóng chỗ nước sâu là v₁ = 0,4 m/s.. Chỗ nước nông hơn (có đĩa), tốc độ truyền sóng là v₂ tùy thuộc bề dày của đĩa (v₂ < v₁). Biết trung trực của S₁S₂ là một vân cực tiểu giao thoa. Giá trị lớn nhất của v2 có thể đạt được là

A. 0,6 m/s    B. 0,9 m/s    C. 0,3 m/s    D. 0,15 m/s

Lời giải:

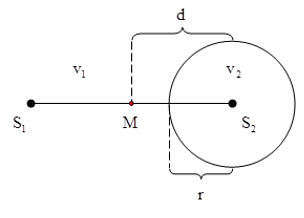
Chọn C.

Giả sử phương trình sóng của nguồn là: u₁ = u₂ =a.cosωt

Sóng do các nguồn truyền đến M lần lượt là:

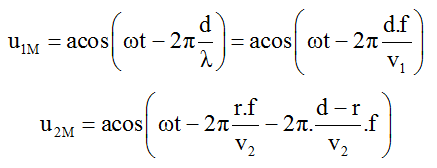
Phương trình dao động tổng hợp tại M:

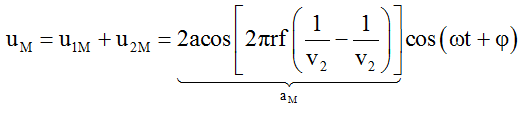
Để M là một cực tiểu giao thoa thì:

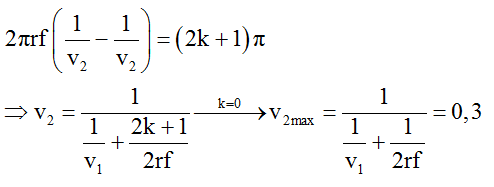
Câu 5: Cho hai nguồn sóng kết hợp S₁, S₂ có phương trình u₁ = u₂¬ = 2acos2t, bước sóng , khoảng cách S₁S₂ = 10 = 12 cm. Nếu đặt nguồn phát sóng S₃ vào hệ trên có phương trình u₃ = acos2t, trên đường trung trực của S₁S₂ sao cho tam giác S₁S₂S₃ vuông. Tại M trên trung trực của S₁S₂ cách trung điểm O của S₁S₂ một đoạn ngắn nhất bằng bao nhiêu dao động với biên độ 5a:

A. 0,245 cm    B. 0,54 cm    C. 1,10 cm     D. 0,122 cm

Lời giải:

Chọn A.

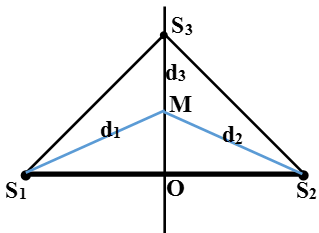
Sóng do các nguồn S₁, S₂, S₃ truyền đến M lần lượt là:

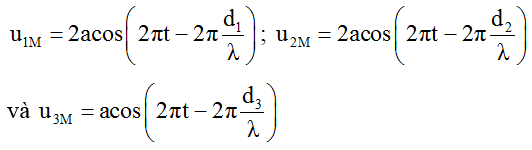
Phương trình dao động tổng hợp tại M:

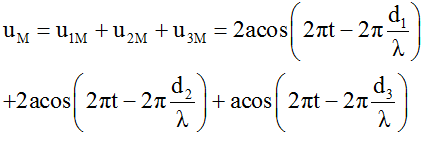
Vì d₁ = d₂ = d nên ta có:

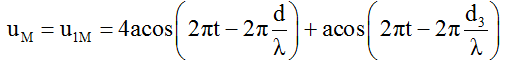
Biên độ dao động sóng tổng hợp tại M là:

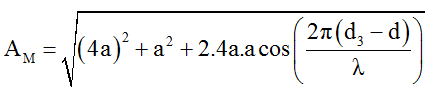
Để AM = 5a thì

Ta có d ≥ S₁O = S₃O ≥ d₃ → d – d₃ ≥ 0 → k ≥ -0,5.

Mặt khác: d₃ – d ≤ S₁S₃ = 6√2

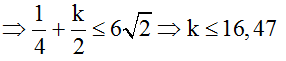
M cáng gần O thì d₃ – d càng nhỏ, do vậy khi M gần O nhất thì k nguyên nhỏ nhất. Do đó kmin = 0.

→ d₃ – d = 0,25cm.

Mặt khác: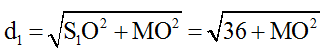

và d₃ = S₃O – MO = 6 – MO

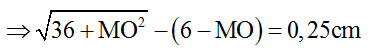
Suy ra MO = 0,245cm.

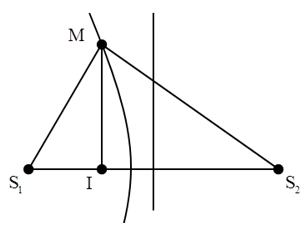
Câu 6: (THPTQG – 2017): Ở mặt nước, tại hai điểm S₁ và S₂ có hai nguồn kết hợp, dao động điều hòa, cùng pha theo phương thẳng đứng. Biết sóng truyền trên mặt nước với bước sóng λ, khoảng cách S₁S₂ = 5,6λ. Ở mặt nước, gọi M là vị trí mà phần tử nước tại đó dao động với biên độ cực đại, cùng pha với dao động của hai nguồn. Khoảng cách ngắn nhất từ M đến đường thẳng S₁S₂ là

A. 0,868λ.    B. 0,852λ.    C. 0,754λ.     D. 0,946λ.

Lời giải:

Chọn C.

+ Điểm M dao động cực đại, cùng pha với nguồn khi:

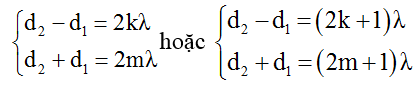
→ d₁ = (m – k)λ

Do đó M gần S₁S₂ nhất khi d_1min = λ khi (m – k)_min = 1

+ Mặt khác d₂ + d₁ > S₁S₂ = 5,6λ

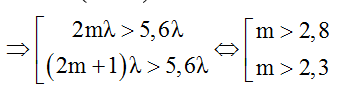
→ m_min = 3 → k_min = 2 (M nằm trên đường cực đại bậc 2)

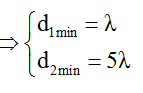
Từ hình học ta có:

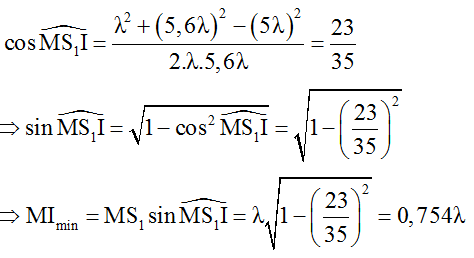
Câu 7: Ở mặt thoáng của chất lỏng có hai nguồn sóng A, B cách nhau 18 cm, dao động theo phương thẳng đứng với phương trình u_A = u_B = a.cos(20πt) (t tính bằng s). Tốc độ truyền sóng trên mặt chất lỏng là 50 cm/s. Gọi M là điểm ở mặt chất lỏng gần A nhất sao cho phần tử chất lỏng tại M dao động với biên độ cực đại và cùng pha với nguồn A. Khoảng cách AM là

A. 2,5 cm    B. 2 cm    C. 5 cm    D. 1,25 cm

Lời giải:

Chọn C.

Bước sóng: λ = v/f = 50/10 = 5cm.

Áp dụng kết quả bài toán điều kiện để một vị trí cực đại và cùng pha với nguồn:

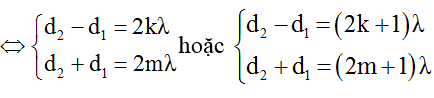
→ d₁ = (m – k)λ

Do đó d_1min khi (m – k)_min = 1 → d_1min = λ = 5cm.

Câu 8: Tại hai điểm A, B trên mặt nước cách nhau 16 cm có hai nguồn phát sóng giống nhau. Điểm M nằm trên mặt nước và trên đường trung trực của AB cách trung điểm I của AB một khoảng nhỏ nhất bằng 4√5 cm luôn dao động cùng pha với I. Điểm N nằm trên mặt nước và nằm trên đường thẳng vuông góc với AB tại A, cách A một khoảng nhỏ nhất bằng bao nhiêu để N dao động với biên độ cực tiểu.

A. 9,22 cm    B. 8,75 cm     C. 2,14 cm    D. 8,57 cm.

Lời giải:

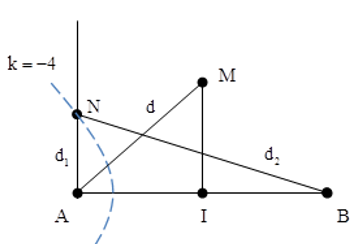
Chọn C.

Vì hai nguồn đồng pha, M, I đều thuộc trung trực của AB nên để M và I dao động cùng pha thì: MA – IA = k.λ

M gần I nhất nên k = 1→ MA = dA = 0,5AB + λ = 8 + λ.

Mặc khác MI = 4√5 cm => MA = 8 + λ =

Số điểm dao động với biên độ cực tiểu trên AB:

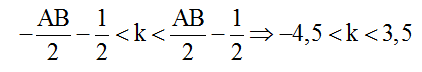
Để N là một điểm cực tiểu và gần A nhất thì N phải nằm trên hypebol cực tiểu có k = -4

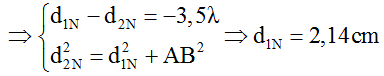
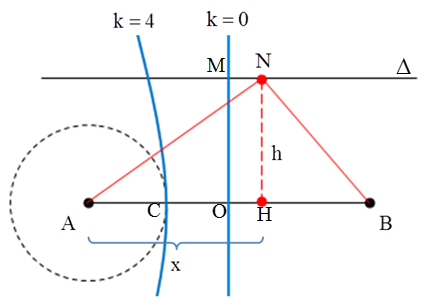
Câu 9: Tại mặt chất lỏng, hai nguồn S₁, S₂ cách nhau 13 cm dao động theo phương thẳng đứng với phương trình u₁ = u₂ = Acos(40πt) (cm) (t tính bằng s). Tốc độ truyền sóng trên mặt chất lỏng là 80 cm/s. Ở mặt chất lỏng, gọi ∆ là đường trung trực của S₁S₂. M là một điểm không nằm trên S₁S₂ và không thuộc ∆, sao cho phần tử chất lỏng tại M dao động với biên độ cực đại và cùng pha với hai nguồn. Khoảng cách ngắn nhất từ M đến ∆ là

A. 2,00 cm.     B. 2,46 cm.    C. 3,07 cm.     D. 4,92 cm.

Lời giải:

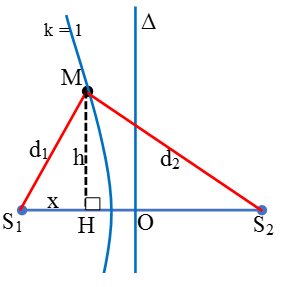
Chọn C.

+ Điều kiện để M dao động cực đại và đồng pha với hai nguồn là:

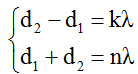
với n, k cùng chẵn hoặc cùng lẻ.

+ Để M gần ∆ nhất thì k = 1, n khi đó có thể nhận các giá trị lẻ 1, 3…..thỏa mãn bất đẳng thức tam giác:

d₁ + d₂ > S₁S₂ =13 => n > 13/λ = 3,25 => n_min = 5 (do n lẻ).

+ Ta có:

+ Từ hình vẽ:

Vậy khoảng cách giữa M và ∆ khi đó bằng HO = OS₁ –S₁H = 13/2 – 3,42 = 3,07cm.

Câu 10: (THPTQG 2018). Ở mặt nước có hai nguồn kết hợp đặt tại hai điểm A và B, dao động cùng pha theo phương thẳng đứng, phát ra hai sóng có bước sóng λ. Trên AB có 9 vị trí mà ở đó các phần tử nước dao động với biên độ cực đại. C và D là hai điểm ở mặt nước sao cho ABCD là hình vuông. M là một điểm thuộc cạnh CD và nằm trên vân cực đại giao thoa bậc nhất (MA – MB = λ). Biết phần tử tại M dao động ngược pha với các nguồn. Độ dài đoạn AB gần nhất với giá trị nào sau đây?

A. 4,3 λ    B. 4,7 λ    C. 4,6 λ    D. 4,4 λ

Lời giải:

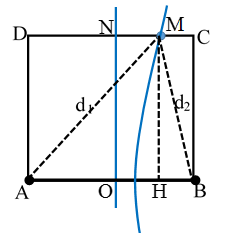
Chọn D.

Đặt AB = a. Hai nguồn đồng pha và trên đoạn AB có 9 cực đại nên 4λ ≤ AB = a < 5λ.

Ta có: AN = NB = √5/2AB => 2√λ < AN < 5√5/2λ .

Vì M là cực đại và ngược pha với nguồn nên ta có:

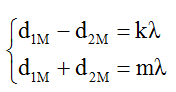
với k, m ϵ Z và k lẻ, n chẵn hoặc k chẵn thì n lẻ.

M là cực đại bậc 1 nên k = 1 → m là số dương chẵn.

Từ hệ trên ta suy ra

Từ hình học, ta được:

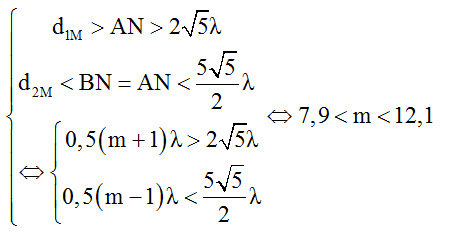
Vì m chẵn nên m = 8; 10 hoặc 12. Ta có bảng giá trị sau:

m	8	10	12
d1M	4,5λ	5,5λ	6,5λ
d2M	3,5 λ	4,5λ	5,5λ

Ta có: AB = AH + HB

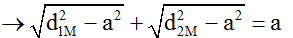
TH1: d₁ = 4,5λ; d₂ = 3,5λ → a = 3,453λ (loại)

TH2: d₁ = 5,5λ; d₂ = 4,5λ → a = 4,376λ (thỏa mãn)

TH3: d₁ = 6,5λ; d₂ = 5,5λ → a = 5,289λ (loại)

Vậy AB = 4,376λ.

Câu 11: Ở mặt chất lỏng có hai nguồn sóng S₁, S₂ cách nhau 19 cm, dao động theo phương thẳng đứng với phương trình là u₁ = u₂ = acos20πt (với t tính bằng s). Tốc độ truyền sóng của mặt chất lỏng là 40 cm/s. Gọi M là điểm ở mặt chất lỏng, gần A nhất sao cho phần từ chất lỏng tại M dao động với biên độ cực đại và cùng pha với các nguồn. Khoảng cách từ M tới AB là

A. 2,86 cm     B. 3,96 cm    C. 1,49 cm     D. 3,18 cm.

Lời giải:

Chọn B.

Bước sóng λ = v/f = 40/10 = 4cm.

Số điểm dao động với biên độ cực đại trên S₁S₂:

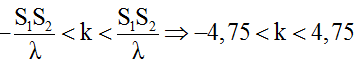
Điều kiện để M dao động cực đại và đồng pha với hai nguồn là:

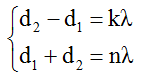
với n, k cùng chẵn hoặc cùng lẻ.

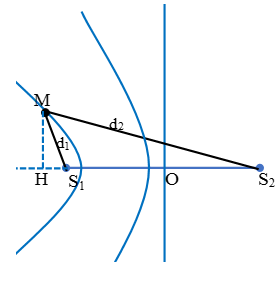
Do đó M gần S₁ nhất nên M thuộc cực đại ngoài cùng (M nằm trên cực đại bậc 4)

Suy ra k = 4 và n phải chẵn.

Mặt khác d₂ + d₁ > S₁S₂ = 19cm → n.λ > 19 ↔ n > 4,75.

Vì n chẵn nên n_min = 6.

+ Khi đó ta có:

Từ hình học ta có: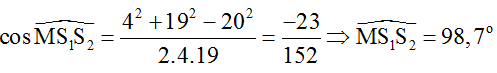

Vậy

Câu 12: Trong thí nghiệm giao thoa sóng mặt nước, hai nguồn kết hợp A, B cách nhau 8 cm dao động cùng pha. Ở mặt nước, có 21 đường dao động với biên độ cực đại và trên đường tròn tâm A bán kính 2,5 cm có 13 phần tử sóng dao động với biên độ cực đại. Đường thẳng (∆) trên mặt nước song song với AB và cách đường thẳng AB một đoạn 5 cm. Đường trung trực của AB trên mặt nước cắt đường thẳng (∆) tại M. Điểm N nằm trên (∆) dao động với biên độ cực tiểu gần M nhất cách M một đoạn d. Giá trị d gần nhất với giá trị nào sau đây?

A. 0,20 cm.    B. 0,36 cm.    C. 0,48 cm.    D. 0,32 cm.

Lời giải:

Chọn D

+ Trên mặt nước có 21 dãy cực đại, như vậy nếu không tính trung trực của AB thì từ H đến A có 10 dãy cực đại.

+ Mặc khác trên đường tròn tâm A bán kính 2,5 cm lại có 13 cực đại điều này chứng tỏ trong đường tròn chứa 6 cực đại (cắt đường tròn tại 12 điểm) và giao điểm giữa đường tròn và AB là một cực đại.

+ Trên đoạn OC các cực đại cách đều nhau nửa bước sóng.

=> OC = 4λ/2 = 4 - 2,5 => λ = 0,75cm

+ Để N gần M nhất thì N thuộc cực tiểu thứ nhất, từ hình vẽ, ta có:

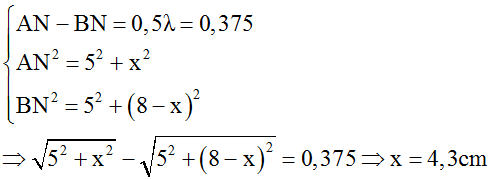
Vậy MN = AH – AO = x – AO = 4,3 – 4 = 0,3cm.

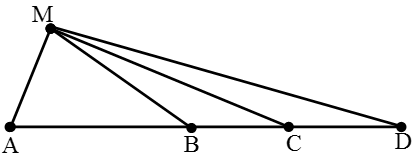
Câu 13: Tại mặt thoáng của một chất lỏng có bốn điểm thẳng hàng được sắp xếp theo thứ thự A, B, C, D với AB = 35cm, BC = 10,5cm, CD = 19,5cm. Điểm M thuộc mặt chất lỏng cách A và C tương ứng là AM = 27,3cm, MC = 36,4cm. Hai nguồn sóng dao động theo phương vuông góc với mặt nước với phương trình u₁ = 3cos100πt cm và u₁ = 4cos100πt cm Biết vận tốc truyền sóng trên mặt chất lỏng bằng 12,3 m/s. Coi biên độ sóng các nguồn truyền đến M bằng biên độ sóng của mỗi nguồn. Khi hai nguồn sóng đặt ở A và C thì các phần tử chất lỏng tại M dao động với biên độ A1, khi hai nguồn sóng đặt tại B và D thì các phần tử chất lỏng tại M dao động với biên độ A₂. Giá trị A₁ và A₂ tương ứng là

A. 2,93 cm và 6,93 cm    B. 5,1 cm và 1,41 cm

C. 5 cm và 2,93 cm    D. 2,93 cm và 7 cm

Lời giải:

Chọn D.

Bước sóng: λ = v/f = 12,3/50 = 0,246m = 24,6cm.

Dễ thấy rằng tam giác AMC vuông tại M, từ đó ta tìm được độ dài của các đoạn thẳng:

MB = 28,7cm; MD = 53,3cm

Phương trình sóng do hai nguồn tại A và B truyền đến M

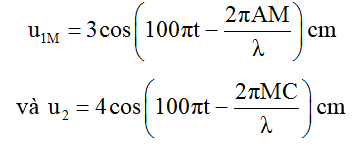
Dao động tổng hợp tại M khi đó có dạng uM = AMcos(100πt + φ).

Với

Áp dụng cho hai trường hợp ta thu được A₁ = 2,93cm và A₂ = 7cm.

Câu 14: Hai nguồn sóng kết hợp trên mặt thoáng chất lỏng dao động theo phương trình u_A = u_B = 4cos10πt mm. Coi biên độ sóng không đổi, tốc độ truyền sóng v = 15cm/s. Hai điểm M, N cùng nằm trên một elip nhận A, B làm tiêu điểm có AM – BM = 1cm; AN – BN = 3,5cm. Tại thời điểm li độ của M là 3mm thì li độ của N tại thời điểm đó là

A. 3mm    B. – 3mm    C. -√3 mm    D. -3√3 mm.

Lời giải:

Chọn D.

Bước sóng: λ = v/f = 15/5 = 3cm.

Phương trình giao thoa sóng:

Tại M:

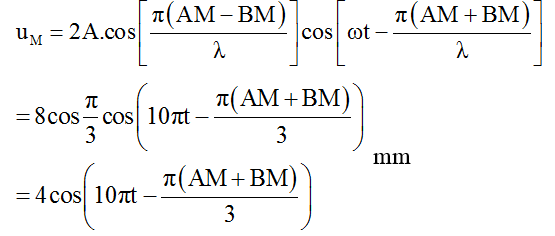
Tại N:

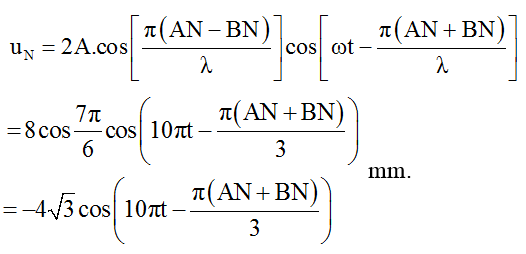
Vì hai điểm M, N cùng nằm trên một elip nhận A, B làm tiêu điểm nên:

AN + BN = AM + BM

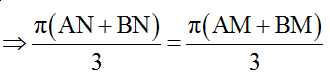
Do đó M và N dao động ngược pha nhau

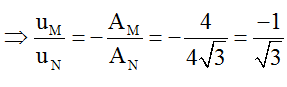
Thời điểm t, u_M = 3mm → u_N = -3√3 mm

Câu 15: Trên mặt chất lỏng có ba nguồn sóng kết hợp dao động theo phương vuông góc với mặt chất lỏng, có phương trình lần lượt là:

u₁ = 7cos(40πt -π/4) ; u₂ = 10cos(40πt - π/6) ; u₃= 4cos(40πt + 5π/6) , và đặt lần lượt tại A, B, C. Biết tam giác ABC cân tại A; AB = AC = 24 cm; BC = 12 cm.

Tốc độ truyền sóng bằng 20 cm/s. Coi biên độ sóng không đổi trong quá trình truyền sóng. Gọi I là trung điểm của BC. Số điểm có biên độ 13 mm trên đoạn AI là

A. 39.    B. 41.    C. 42.    D. 40.

Lời giải:

Chọn B.

Ta có: λ = v/f = 1cm ;

Xét điểm M bất kỳ trên AI ta có u₂M và u₃M ngược pha nhau nên:

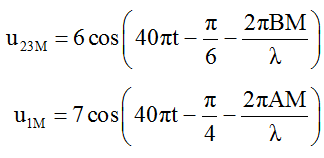
Điểm M có biên độ 13cm = 6 + 7 cm thì:

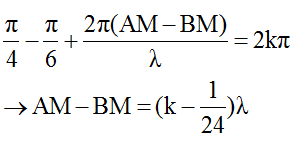
M nằm trong khoảng AI nên ta có

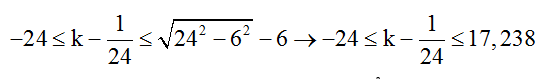
=> -23,958 < k ≤ 17,2795

=> có 41 điểm.