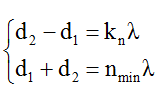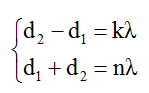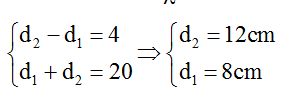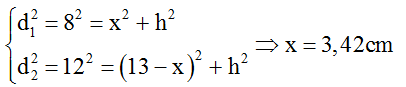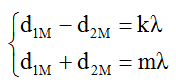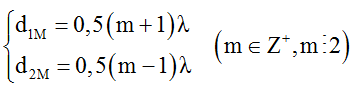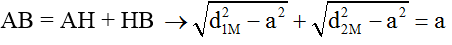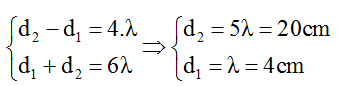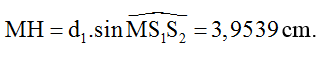Cách xác định vị trí của điểm cực đại cùng pha, ngược pha với nguồn trong giao thoa sóng hay, chi tiết - Vật Lí lớp 12
Cách xác định vị trí của điểm cực đại cùng pha, ngược pha với nguồn trong giao thoa sóng hay, chi tiết
Với Cách xác định vị trí của điểm cực đại cùng pha, ngược pha với nguồn trong giao thoa sóng hay, chi tiết Vật Lí lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập xác định vị trí của điểm cực đại cùng pha, ngược pha với nguồn trong giao thoa sóng từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

A. Phương pháp giải
1. Điều kiện cho điểm cực đại dao động cùng pha, ngược pha với hai nguồn đồng pha.
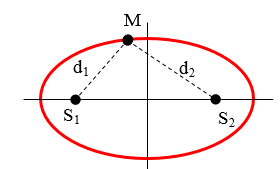
+ Phương trình sóng tại 2 nguồn cùng biên độ A: (Điểm M cách hai nguồn lần lượt d1, d2)
u1 = Acos(2πft +φ) và u2 = Acos(2πft +φ)
+ Phương trình giao thoa sóng tại M:
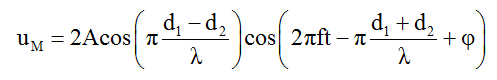
+ Điều kiện để M dao động cực đại và đồng pha với hai nguồn:
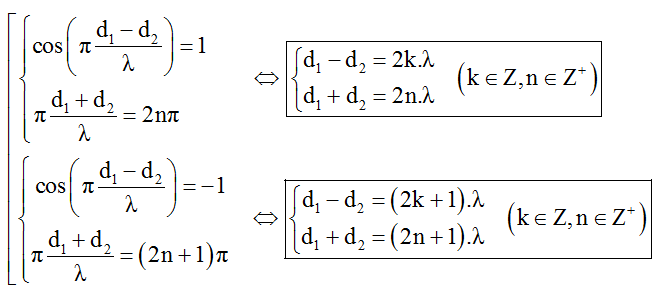
+ Điều kiện để M dao động cực đại và ngược pha với hai nguồn:
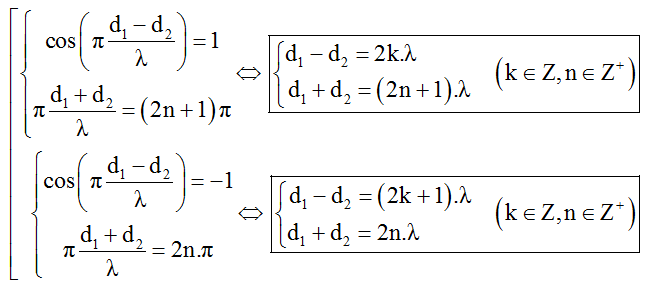
* Tổng quát hóa:
+ Điều kiện để M dao động với biên độ cực đại và cùng pha với nguồn là:
- Cực đại: d1 – d2 = k.λ.
- Cùng pha: d1 + d2 = n.λ
Với k và n hoặc cùng chẵn hoặc cùng lẻ.
+ Điều kiện để M dao động với biên độ cực đại và ngược pha với nguồn là:
- Cực đại: d1 – d2 = k.λ.
- Cùng pha: d1 + d2 = n.λ
Với k, n là chẵn lẻ (k lẻ thì n chẵn hoặc ngược lại).
2. Khoảng cách gần nhất từ điểm cực đại đồng pha, ngược pha với nguồn tới đoạn nối 2 nguồn và đường trung trực của hai nguồn.
* Xét bài toán có điểm M dao động cực đại và đồng pha với nguồn.
a) Xác định điểm M gần nhất với nguồn S1 (hoặc tới đoạn thẳng nối 2 nguồn) khi 2 nguồn cùng pha.
Bước 1: Xác định số vân cực đại trên đoạn nối 2 nguồn qua bất phương trình tìm k ϵ Z sau:
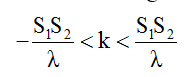
Suy ra cực đại ngoài cùng có k có độ lớn bằng |kn| = [S1S2/λ]
Bước 2: Viết điều kiện để điểm M cực đại và đồng pha với hai nguồn.
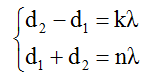
với n, k cùng chẵn hoặc cùng lẻ.
Vì M gần nguồn S1 nhất (hoặc gần S1S2 nhất) nên M thuộc cực đại ngoài cùng.
Suy ra k = kn. Do đó nếu kn lẻ thì n phải lẻ hoặc nếu kn chẵn thì n chẵn.
Bước 3: Xác định d1 và d2:
+ Tìm giá trị của n qua bất đẳng thức tam giác: d1 + d2 > S1S2
⇔ n > S1S2/λ. Tùy theo n chẵn hay lẻ, ta chọn giá trị nguyên nhỏ nhất n = nmin.
+ Giải hệ phương trình:
Ta tìm được d1; d2. Suy ra MS1min = d1.
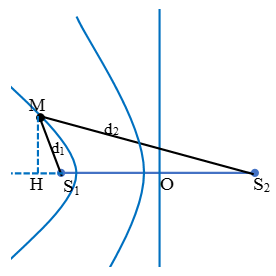
Bước 4: Tìm khoảng cách từ M đến S1S2.
Dựa vào định lý hàm số cos trong ∆MS1S2 ta xác định góc :
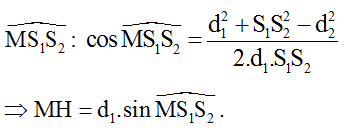
b) Xác định điểm M gần nhất với đường trung trực của hai nguồn khi 2 nguồn cùng pha.
+ M dao động cực đại gần đường trung trực của S1S2 nhất khi M thuộc cực đại bậc 1.
Do đó M cần tìm có điều kiện: 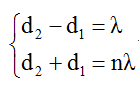
+ Tìm giá trị của n qua bất đẳng thức tam giác: d1 + d2 > S1S2
⇔ n > S1S2/λ . Ta chọn giá trị nguyên lẻ nhỏ nhất n = nmin.
+ Giải hệ phương trình: ta tìm được d1; d2.
Từ hình vẽ: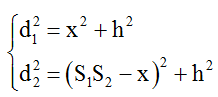
Vậy khoảng cách giữa M và ∆ khi đó bằng HO = OS1 –S1H = 0,5S1S2 – x.
* Xét bài toán có điểm M dao động cực đại và ngược pha với nguồn.
Ta làm tương tự như trường hợp trên với điều kiện cho điểm M cực đại ngược pha với hai nguồn là: 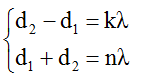
B. Ví dụ minh họa
Ví dụ 1: (THPTQG – 2017): Ở mặt nước, tại hai điểm S1 và S2 có hai nguồn kết hợp, dao động điều hòa, cùng pha theo phương thẳng đứng. Biết sóng truyền trên mặt nước với bước sóng λ, khoảng cách S1S2 = 5,6λ. Ở mặt nước, gọi M là vị trí mà phần tử nước tại đó dao động với biên độ cực đại, cùng pha với dao động của hai nguồn. Khoảng cách ngắn nhất từ M đến đường thẳng S1S2 là
A. 0,868λ. B. 0,852λ. C. 0,754λ. D. 0,946λ.
Hướng dẫn giải:
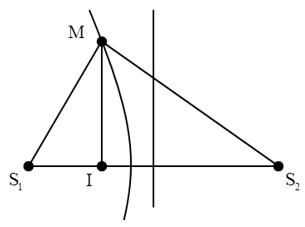
Chọn C.
+ Điểm M dao động cực đại, cùng pha với nguồn khi:
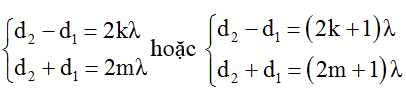
→ d1 = (m – k)λ
Do đó M gần S1S2 nhất khi d1min = λ khi (m – k)min = 1
+ Mặt khác d2 + d1 > S1S2 = 5,6λ
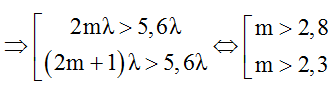
→ mmin= 3 → kmin = 2 (M nằm trên đường cực đại bậc 2)
=> d1min = λ; d2min = 5λ
Từ hình học ta có:
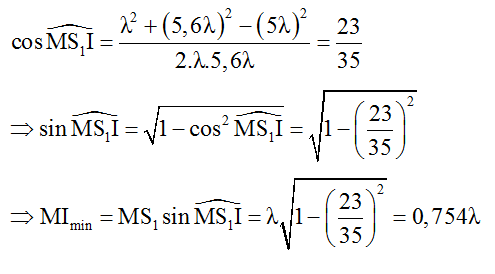
C. Bài tập vận dụng
Câu 1: Ở mặt thoáng của chất lỏng có hai nguồn sóng A, B cách nhau 18 cm, dao động theo phương thẳng đứng với phương trình uA = uB = a.cos(20πt) (t tính bằng s). Tốc độ truyền sóng trên mặt chất lỏng là 50 cm/s. Gọi M là điểm ở mặt chất lỏng gần A nhất sao cho phần tử chất lỏng tại M dao động với biên độ cực đại và cùng pha với nguồn A. Khoảng cách AM là
A. 2,5 cm B. 2 cm C. 5 cm D. 1,25 cm
Lời giải:
Chọn C.
Bước sóng: λ = v/f = 50/10 = 5cm.
Áp dụng kết quả bài toán điều kiện để một vị trí cực đại và cùng pha với nguồn:
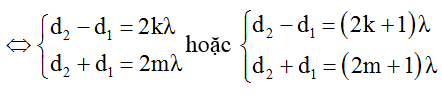
→ d1 = (m – k)λ
Do đó d1min khi (m – k)min = 1 → d1min = λ = 5cm.
Câu 2: Tại hai điểm A, B trên mặt nước cách nhau 16 cm có hai nguồn phát sóng giống nhau. Điểm M nằm trên mặt nước và trên đường trung trực của AB cách trung điểm I của AB một khoảng nhỏ nhất bằng 4√5 cm luôn dao động cùng pha với I. Điểm N nằm trên mặt nước và nằm trên đường thẳng vuông góc với AB tại A, cách A một khoảng nhỏ nhất bằng bao nhiêu để N dao động với biên độ cực tiểu.
A. 9,22 cm B. 8,75 cm C. 2,14 cm D. 8,57 cm.
Lời giải:
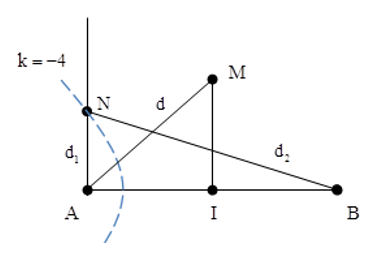
Chọn C.
Vì hai nguồn đồng pha, M, I đều thuộc trung trực của AB nên để M và I dao động cùng pha thì: MA – IA = k.λ
M gần I nhất nên k = 1→ MA = dA = 0,5AB + λ = 8 + λ.
Mặc khác MI = 4√5 cm
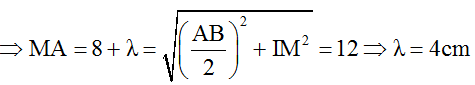
Số điểm dao động với biên độ cực tiểu trên AB:
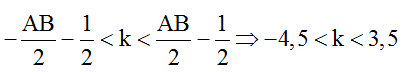
Để N là một điểm cực tiểu và gần A nhất thì N phải nằm trên hypebol cực tiểu có k = -4
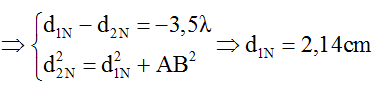
Câu 3: Tại mặt chất lỏng, hai nguồn S1, S2 cách nhau 13 cm dao động theo phương thẳng đứng với phương trình u1 = u2 = Acos(40πt) (cm) (t tính bằng s). Tốc độ truyền sóng trên mặt chất lỏng là 80 cm/s. Ở mặt chất lỏng, gọi ∆ là đường trung trực của S1S2. M là một điểm không nằm trên S1S2 và không thuộc ∆, sao cho phần tử chất lỏng tại M dao động với biên độ cực đại và cùng pha với hai nguồn. Khoảng cách ngắn nhất từ M đến ∆ là
A. 2,00 cm. B. 2,46 cm. C. 3,07 cm. D. 4,92 cm.
Lời giải:
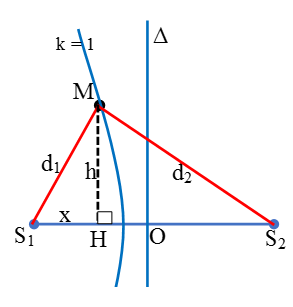
Chọn C.
+ Điều kiện để M dao động cực đại và đồng pha với hai nguồn là:
với n, k cùng chẵn hoặc cùng lẻ.
+ Để M gần ∆ nhất thì k = 1, n khi đó có thể nhận các giá trị lẻ 1, 3…..thỏa mãn bất đẳng thức tam giác:
d1 + d2 > S1S2 = 13 => n > 13/λ = 3,25 => nmin = 5 (do n lẻ).
+ Ta có:
+ Từ hình vẽ:
Vậy khoảng cách giữa M và ∆ khi đó bằng HO = OS1 –S1H = 13/2 – 3,42 = 3,07cm.
Câu 4: (THPTQG 2018). Ở mặt nước có hai nguồn kết hợp đặt tại hai điểm A và B, dao động cùng pha theo phương thẳng đứng, phát ra hai sóng có bước sóng λ. Trên AB có 9 vị trí mà ở đó các phần tử nước dao động với biên độ cực đại. C và D là hai điểm ở mặt nước sao cho ABCD là hình vuông. M là một điểm thuộc cạnh CD và nằm trên vân cực đại giao thoa bậc nhất (MA – MB = λ). Biết phần tử tại M dao động ngược pha với các nguồn. Độ dài đoạn AB gần nhất với giá trị nào sau đây?
A. 4,3 λ B. 4,7 λ C. 4,6 λ D. 4,4 λ
Lời giải:
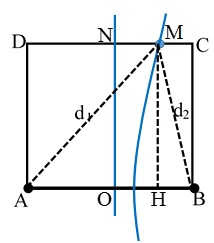
Chọn D.
Đặt AB = a. Hai nguồn đồng pha và trên đoạn AB có 9 cực đại nên 4λ ≤ AB = a < 5λ.
Ta có: AN = NB = √5/2 AB => 2√5λ < AN < 5√5/2λ .
Vì M là cực đại và ngược pha với nguồn nên ta có:
với k, m ϵ Z và k lẻ, n chẵn hoặc k chẵn thì n lẻ.
M là cực đại bậc 1 nên k = 1 → m là số dương chẵn.
Từ hệ trên ta suy ra
Từ hình học, ta được:
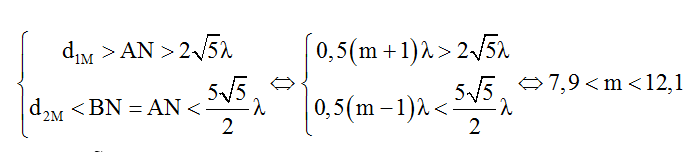
Vì m chẵn nên m = 8; 10 hoặc 12. Ta có bảng giá trị sau:
| m | 8 | 10 | 12 |
| d1M | 4,5λ | 5,5λ | 6,5λ |
| d2M | 3,5 λ | 4,5λ | 5,5λ |
Ta có:
TH1: d1 = 4,5λ; d2 = 3,5λ → a = 3,453λ (loại)
TH2: d1 = 5,5λ; d2 = 4,5λ → a = 4,376λ (thỏa mãn)
TH3: d1 = 6,5λ; d2 = 5,5λ → a = 5,289λ (loại)
Vậy AB = 4,376λ.
Câu 5: Ở mặt chất lỏng có hai nguồn sóng S1, S2 cách nhau 19 cm, dao động theo phương thẳng đứng với phương trình là u1 = u2 = acos20πt (với t tính bằng s). Tốc độ truyền sóng của mặt chất lỏng là 40 cm/s. Gọi M là điểm ở mặt chất lỏng, gần A nhất sao cho phần từ chất lỏng tại M dao động với biên độ cực đại và cùng pha với các nguồn. Khoảng cách từ M tới AB là
A. 2,86 cm B. 3,96 cm C. 1,49 cm D. 3,18 cm.
Lời giải:
Chọn B.
Bước sóng λ = v/f = 40/10 = 4cm.
Số điểm dao động với biên độ cực đại trên S1S2:
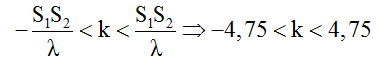
Điều kiện để M dao động cực đại và đồng pha với hai nguồn là:
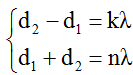
với n, k cùng chẵn hoặc cùng lẻ.
Do đó M gần S1 nhất nên M thuộc cực đại ngoài cùng (M nằm trên cực đại bậc 4)
Suy ra k = 4 và n phải chẵn.
Mặt khác d2 + d1 > S1S2 = 19cm → n.λ > 19 ↔ n > 4,75.
Vì n chẵn nên nmin = 6.
+ Khi đó ta có:
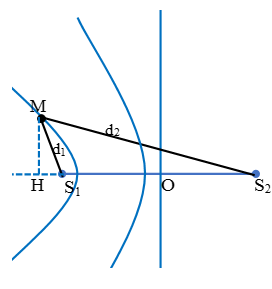
Từ hình học ta có:
Vậy