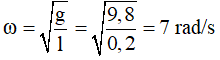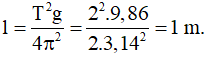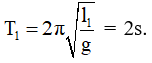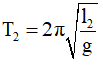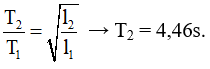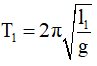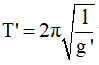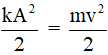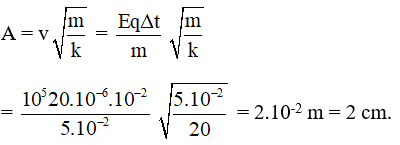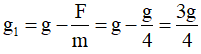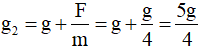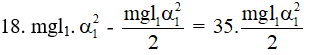Các dạng bài tập Con lắc đơn có lời giải - Vật Lí lớp 12

---

Các dạng bài tập Con lắc đơn có lời giải

Với Các dạng bài tập Con lắc đơn có lời giải Vật Lí lớp 12 tổng hợp các dạng bài tập, 150 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Con lắc đơn từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

• Lý thuyết Con lắc đơn Xem chi tiết
• Bài tập Con lắc đơn trong đề thi Đại học có giải chi tiết Xem chi tiết

• Dạng 1: Viết phương trình dao động của Con lắc đơn

  Xem chi tiết

• Dạng 2: Chu kì con lắc đơn thay đổi

  Xem chi tiết

• Dạng 3: Con lắc trùng phùng

  Xem chi tiết

• Dạng 4: Năng lượng con lắc đơn và lực căng dây

  Xem chi tiết

• Bài toán va chạm trong con lắc đơn và con lắc đơn đứt dây hay và khó

  Xem chi tiết

• 60 Bài tập trắc nghiệm Con lắc đơn có lời giải

  Xem chi tiết

Cách viết phương trình dao động của Con lắc đơn

A. Phương pháp & Ví dụ

1. Phương pháp

Phương trình dao động con lắc đơn: S = S_ocos(ωt + Φ) hoặc a = a_ocos(ωt + j)(rad)

Bước 1: Tìm t

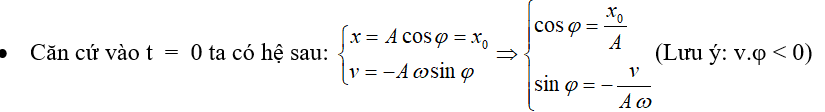
Chú ý: t = 0, vật đi theo chiều (+) thì và ngược lại nếu vật đi theo chiều (-) thì φ > 0

Bước 2: Tìm ω > 0 nếu các đáp án khác nhau về ω

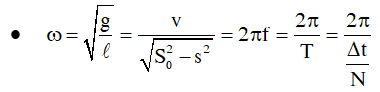
Bước 3: Tìm S_o > 0 nếu các đáp án khác nhau về S_o

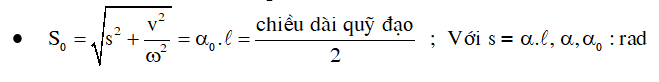
2. Ví dụ

Ví dụ 1: Con lắc đơn có T = 2s. Trong quá trình dao động, góc lệch cực đại của dây là 0,04 rad. Chọn gốc thời gian là lúc vật có li độ là α = 0,02 rad và đang chuyển động về VTCB. PHương trình dao động của con lắc là

A. α = 0,04cos(πt+π/3)(rad).          B. α = 0,04cos(πt-π/3)(rad).

C. α = 0,04cos(πt+2π/3)(rad).          D. α = 0,04cos(πt-2π/3)(rad).

Hướng dẫn:

t = 0 ⇒

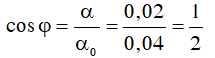
Vật đang ở li độ góc dương đi về VTCB tức là đi theo chiều (-)

⇒ φ = π/3 > 0

Ví dụ 2: Một con lắc đơn được kích thích và để cho dao động tự do với biên độ góc nhỏ trong điều kiện lực cản không đáng kể thì dao động điều hòa với tần số 0,25Hz. Con lắc dao động với biên độ 4cm. Chọn gốc thời gian là lúc con lắc qua VTCB theo chiều dương thì biểu thức li độ góc α là

A. α = 0,04cos(πt-π/2) (rad).          B. α = 0,01cos(πt-π/2) (rad).

C. α = 0,16cos(πt) (rad).          D. α = 0,04cos(πt) (rad).

Hướng dẫn:

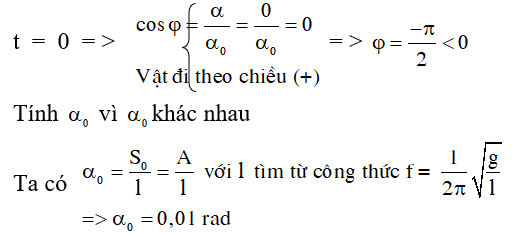
B. Bài tập trắc nghiệm

Câu 1. Một con lắc đơn có chiều dài l = 16 cm. Kéo con lắc lệch khỏi vị trí cân bằng một góc 9° rồi thả nhẹ. Bỏ qua mọi ma sát, lấy g = 10 m/s², π² = 10. Chọn gốc thời gian lúc thả vật, chiều dương cùng chiều với chiều chuyển động ban đầu của vật. Viết phương trình dao động theo li độ góc tính ra rad.

A. α = 0,157cos(2,5π + π) rad

B. α = 0,314cos(2,5π + π/2) rad

C. α = 0,314cos(5π - π/2) rad

D. α = 0,157cos(5π + π) rad

Lời giải:

Ta có:

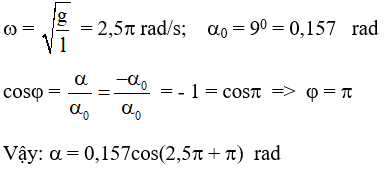
Chọn A

Câu 2. Một con lắc đơn dao động điều hòa với chu kì T = 2 s. Lấy g = 10 m/s², π² = 10. Viết phương trình dao động của con lắc theo li độ dài. Biết rằng tại thời điểm ban đầu vật có li độ góc α = 0,05 rad và vận tốc v = - 15,7 cm/s

A. s = 5√2cos(2πt - π/4) cm

B. s = 5cos(πt + 3π/4) cm

C. s = 5cos(2πt - π/4) cm

D. s = 5√2cos(πt + π/4) cm

Lời giải:

Ta có:

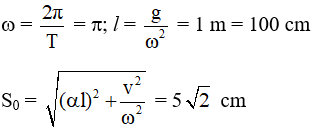
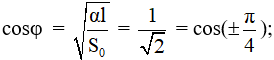
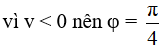
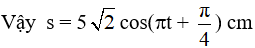
Chọn D

Câu 3. Một con lắc đơn treo một vật nặng có khối lượng 100 g, chiều dài dây treo là 1 m, treo tại nơi có g = 9,86 m/s². Bỏ qua mọi ma sát. Kéo con lắc lệch khỏi vị trí cân bằng góc α₀ rồi thả không vận tốc đầu. Biết con lắc dao động điều hòa với năng lượng W = 8.10^-4 J. Lập phương trình dao động điều hòa của con lắc, chọn gốc thời gian lức vật nặng có li độ cực đại dương. Lấy π² = 10

A. s = 2cosπt cm

B. s = 4cos(πt + π) cm

C. s = 4cosπt cm

D. s = 2cos(πt + π/3) cm

Lời giải:

Phương trình dao động: s = S₀cos(ωt + φ)

Tần số góc ω = √(g/l) = √(9,86) = π rad

Từ W = (mω²S₀²)/2 suy ra biên độ dao động S₀

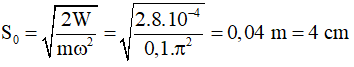
Tìm φ : t = 0, s = S₀ ⇒ cosφ = 1 ⇒ φ = 0. Vậy s = 4cosπt cm. Chọn C.

Câu 4. Một con lắc đơn dài l = 20 cm treo tại một điểm có định. Kéo con lắc khỏi phương thẳng đứng một góc bằn 0,1 rad về phía bên phải rồi chuyền cho một vận tốc 14 cm/s theo phương vuông góc với dây về phía vi trí cân bằng. Coi con lắc dao động điều hòa, viết phương trình dao động đối với li độ dài của con lắc. Chọn gốc tọa độ tại vị trí cân bằng, chiều dương hướng từ vị trí cân bằng sang phía bên phải, gốc thời gian là lúc con lắc đi qua vị trí cân bằng lần thứ nhất. Cho gia tốc trọng trường g = 9,8 m/s²

A. s = 2cos(7t + π/3) cm

B. s = 2cos(7t + π/2) cm

C. s = 2√2cos(7t + π/2) cm

D. s = 2√3cos(7t - π/2 cm

Lời giải:

Phương trình dao động: s = S₀cos(ωt + φ)

Tần số góc:

Từ

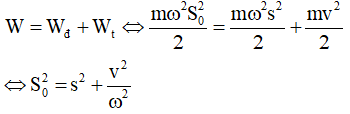
Với s = αl, v = 14 cm/s ⇒ S₀ = 2√2 cm.

Tại thời điểm t = 0 lúc con lắc qua vị trí cân bằng lần thứ nhất nên s = 0, v < 0:

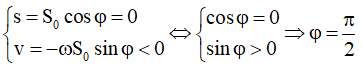
Vậy phương trình dao động của con lắc là: s = 2√2cos(7t + π/2) cm. Chọn C

Câu 5. Một con lắc đơn đang nằm yên tại vị trí cân bằng, truyền cho nó một vận tốc v₀ = 40 cm/s theo phương ngang thì con lắc đơn dao động điều hòa. Biết rằng tại vị trí có li độ góc α = 0,1√3 rad thì nó có vận tốc v = 20 cm/s. Lấy g = 10 m/s². Chọn gốc thời gian là lúc truyền vận tốc cho vật, chiều dương cùng chiều với vận tốc ban đầu. Viết phương trình dao động của con lắc theo li độ dài.

A. s = 8√2cos(5t - π/2) cm

B. s = 8cos(5t + π/2) cm

C. s = 8√2cos(5t - π/2) cm

D. s = 8cos(5t - π/2) cm

Lời giải:

Ta có:

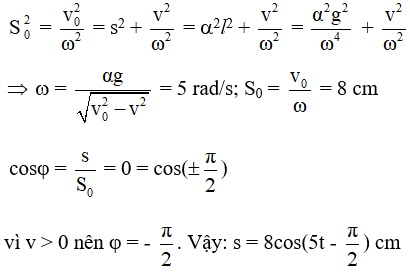
Chọn D

Câu 6. Con lắc đơn dao động điều hòa với chu kì T = π/5 s. Biết rằng ở thời điểm ban đầu con lắc ở vị trí biên, có biên độ góc α₀ với cosα₀ = 0,98. Lấy g = 10 m/s². Viết phương trình dao động của con lắc theo li độ góc.

A. α = 0,2cos10t rad.

B. α = 0,1cos10t rad.

C. α = 0,2cos(10t + π) rad.

D. α = 0,1cos(10t + π) rad.

Lời giải:

Ta có: ω = 2π/T = 10 rad/s; cosα₀ = 0,98 = cos11,48° ⇒ α₀ = 11,48° = 0,2 rad

cosφ = α/α₀ = α₀/α₀ = 1 = cos0 ⇒ = 0. Vậy α = 0,2cos10t rad. Chọn A

Câu 7. Một con lắc đơn gồm quả cầu nặng 200 g, treo vào đầu sợi dây dài l . Tại nơi có g = 9,86 m/s² con lắc dao động với biên độ nhỏ và khi qua vị trí cân bằng có vận tốc v₀ = 6,28 cm/s và khi vật nặng đi từ vị trí cân bằng đến li độ α = 0,5α₀ mất thời gian ngắn nhất là 1/6 s. Viết phương trình dao động của con lắc, biết tại t = 0 thì α = α₀ , đồng thời quả cầu đang chuyển động ra xa vị trí cân bằng. Bỏ qua ma sát và sức cản không khí.

A. s = 2cos(πt + π/3) cm

B. s = 2√2cos(πt + π/3) cm

C. s = 2cos(πt - π/3) cm

D. s = 2√2cos(πt - π/3) cm

Lời giải:

Dùng liên hệ chuyển động tròn đều và dao động điều hòa ta tính được thời gian vật nặng đi từ vị trí câng bằng đến li độ α = 0,5α₀ (hay s = 0,5S₀) mất hời gian ngắn nhất là T/12 = 1/6 ⇒ T = 2 s

Chiều dài của con lắc

Phương trình dao động của con lắc là s = S₀cos(ωt + φ)

Tần số góc: ω = π rad/s.

Vận tốc con lắc khi qua vị trí cân bằng v_max = ωS₀ = 6,28 ⇒ S₀ = 2 cm

Tại thời điểm t = 0, α = 0,5α₀ ⇒ s = 0,5S₀, quả cầu đang chuyển động ra xa vị trí cân bằng nên khi đó quả cầu đi theo chiều dương (v > 0):

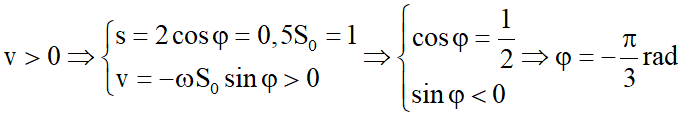
Vậy phương trình dao động của con lắc s = 2cos(πt + π/3) cm. Chọn C

Câu 8. Một con lắc đơn có chiều dài l = 40 cm , được treo tại nơi có g = 10 m/s². Bỏ qua sức cản không khí. Đưa con lắc lệch khỏi VTCB một góc 0,1 rad rồi truyền cho vật nặng vận tốc 20 cm/s theo phương vuông góc với dây hướng về VTCB. Chọn gốc tọa độ tại vị trí cân bằng của vật nặng, gốc thời gian lúc gia tốc của vật nặng tiếp tuyến với quỹ đạo lần thứ nhất. Viết phương trình dao động của con lắc theo li độ cong

A. 8cos(25t + π) cm

B. 4√2cos(25t + π) cm

C. 4√2cos(25t + π/2) cm

D. 8cos(25t) cm

Lời giải:

Phương trình dao động của con lắc theo li độ cong có dạng: s = S_maxcos(ωt + φ)

Gọi α_m là biên độ góc của dao độngn của con lắc đơn

Khi đo biên độ của tọa độ cong S_max = α_m.l → α₀ = 0,1 rad

Theo ĐL bảo toàn năng lượng ta có :

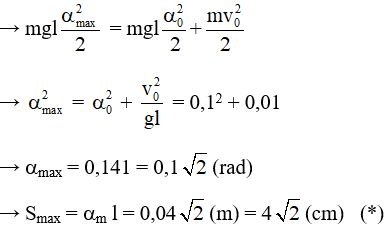
Tần số góc của dao động ω = √(g/l) = 25 rad/s

Gốc thời gian t = 0 khi gia tốc của vật nặng tiếp tuyến với quỹ đạo lần thứ nhất tức là gia tốc hướng tâm a_ht = 0 → v = 0: tức là lúc vật ở biên âm (ở điểm A).

Khi t = 0, s = -S_max → φ = π

Vậy: s = 4√2cos( ωt + π) (cm). Chọn đáp án B

Câu 9. Treo một con lắc đơn tại nơi có gia tốc g = π² m/s², chiều dài của dây treo là 1 m và bỏ qua tác dụng của lực cản. Kéo vật lệch ra khỏi vị trí cân bằng một góc 6° rồi thả nhẹ cho vật dao động điều hòa. Chọn gốc thời gian là lúc buông vật, chiều dương là chiều chuyển động của vật ngay khi buông vật. Phương trình dao động của vật nhỏ là:

A. s = (π/30)cos(πt + π) m

B. s = (π/30)cos(πt) m

C. s = 0,06cos(πt) m

D. s = 0,06cos(πt + π) m

Lời giải:

Biên độ của dao động s = l.φ = l.(π/30) = π/30 rad

Tần số góc của dao động ω = √(g/l) = π rad/s

Vậy s = (π/30)cos(πt + π) m . Chọn A

Câu 10. Con lắc đơn dao động điều hòa theo thời gian có ly độ góc mô tả theo hàm cosin với biên độ góc α₀, tần số góc ω và pha ban đầu φ. Chiều dài giây treo là l. Phương trình ly độ góc biến thiên theo thời gian có dạng

A. α = α₀cos(ωt + φ)

B. α = ωα₀cos(ωt + φ)

C. α = ω²α₀cos(ωt + φ)

D. α = lα₀cos(ωt + φ)

Lời giải:

Phương trình li độ góc biến thiên theo quy luật α = α₀cos(ωt + φ). Chọn A.

Câu 11. (Minh họa – 2017) Một con lắc đơn có chiều dài 1 m, được treo tại nơi có gia tốc trọng trường g = π² m/s². Giữ vật nhỏ của con lắc ở vị trí có li độ góc −9° rồi thả nhẹ vào lúc t = 0. Phương trình dao động của vật là

A. s = 5cos(πt + π) cm

B. s = 5cos(2πt) cm

C. s = 5πcos(πt + π) cm

D. s = 5πcos(2πt) cm

Lời giải:

Tần số góc của dao động ω = √(g/l) = √((π²)/l) = π rad/s

Biên độ cong của dao động s₀ = lα₀ = l.(9°/180°).π = 5π cm

Ban đầu vật ở vị trí biên âm, do vậy phương trình dao động sẽ là s = 5πcos(πt + π) cm. Chọn C

Cách giải bài tập Chu kì con lắc đơn thay đổi theo chiều dài, nhiệt độ, độ cao, gia tốc trọng trường

A. Phương pháp & Ví dụ

2.1. Thay đổi chiều dài con lắc đơn

    + Cắt nối chiều dài con lắc đơn

    + Tăng giảm nhiệt độ

    + Con lắc vướng đinh

1. Phương pháp

Chu kỳ con lắc ban đầu khi chưa có sự thay đổi

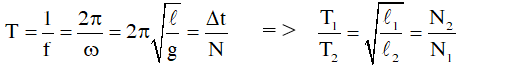
Nếu con lắc đơn có l₁,T₁ và l₂,T₂ thì: chu kì con lắc khi

• Nối chiều dài con lắc: l = al₁+ bl₂ ⇒ T² = aT₁² + bT₂²

• Cắt chiều dài con lắc : l = al₁- bl₂ (với l₁ > l₂) ⇒ T² = aT₁² - bT₂²

Dây treo làm bằng kim loại nên chiều dài thay đổi theo nhiệt độ

• l = l_o(1 + λt)

Trong đó:

    + λ: hệ số nở dài của con lắc

    + l_o: chiều dài ở 0^οC

• Chu kỳ con lắc dao động ĐÚNG ở nhiệt độ t₁ (^οC):

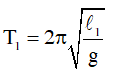
• Chu kỳ con lắc dao động SAI ở nhiệt độ t₂ (^οC):

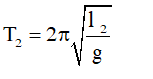
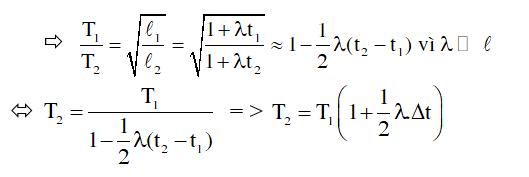
Chú ý:

    + Khi nhiệt độ tăng thì chiều dài con lắc tăng nên chu kỳ dao động tăng lên ⇒ Đồng hồ chạy chậm.

    + Khi nhiệt độ giảm thì chiều dài con lắc giảm nên chu kỳ dao động giảm xuống ⇒ Đồng hồ chạy nhanh.

Con lắc vướng đinh, bị kẹp chặt

• Chu kỳ con lắc trước khi vướng đinh: l₁: chiều dài con lắc trước khi vướng đinh

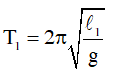
• Chu kỳ con lắc sau khi vướng đinh: l₂: chiều dài con lắc sau khi vướng đinh

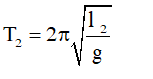
Chu kỳ của con lắc:

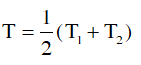
2. Ví dụ

Ví dụ 1: Một con lắc đơn có độ dài bằng l. Trong khoảng thời gian Δt nó thực hiện 12 dao động. Khi giảm độ dài của nó bớt 16cm, trong cùng khoảng thời gian Δt như trên, con lắc thực hiện 20 dao động. Cho biết g = 9,8 m/s². Tính độ dài ban đầu của con lắc.

A. 40cm          B. 60cm         C. 50cm         D. 25cm

Hướng dẫn:

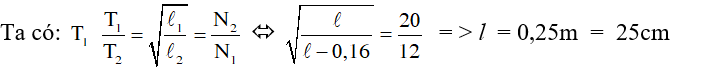
Ví dụ 2: Một con lắc có độ dài l₁ dao động với chu kỳ T₁ = 0,8s. Một con lắc đơn khác có độ dài l₂ dao động với chu kỳ T₂ = 0,6s. Chu kỳ con lắc đơn có chiều dài l₁ + l₂ là

A. 0,7s          B. 0,8s         C. 1s          D. 1,4s.

Hướng dẫn:

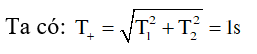
Ví dụ 3: Một con lắc đơn có dây treo bằng kim loại, hệ số dãn nở của kim loại này là 1,4.10^-5 độ^-1, con lắc đơn dao động tại một điểm cố định trên mặt đất, có chu kỳ 2s lúc ở 10^οC. Nếu tăng nhiệt độ thêm 20^οC thì chu kỳ sẽ

A. tăng 2,8.10^-4.          B. giảm 2,8.10^-4.

C. tăng 4,2.10^-4.          D. giảm 4,2.10^-4.

Hướng dẫn:

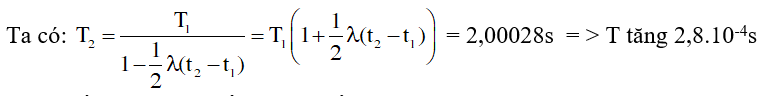
Ví dụ 4: Con lắc đơn đặt tại bề mặt trái đất chạy đúng khi nhiệt độ là 0^οC. Hỏi khi đưa con lắc xuống một tàu ngầm ở độ sâu 4,8km so với bề mặt trái đất và nhiệt độ là 25^οC thì mỗi ngày đêm con lắc chạy nhanh hay chậm là bao nhiêu? Cho biết hệ số dãn nở là 10^-5độ^-1, bán kính trái đất R = 6400km.

A. nhanh 21,6s.          B. chậm 43,2s.          C. nhanh 43,2s.           D. chậm 21,6s.

Hướng dẫn:

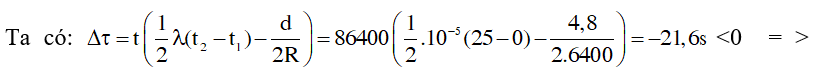
Chạy chậm 21,6s

Ví dụ 5: Kéo con lắc đơn có chiều dài 1m ra khỏi vị trí cân bằng một góc nhỏ so với phương thẳng đứng rồi thả nhẹ cho dao động. Khi đi qua vị trí cân bằng, dây treo bị vướng vào một chiếc đinh đóng dưới điểm treo con lắc một đoạn 36cm. Lấy g = 10m/s². Chu kỳ dao động của con lắc là?

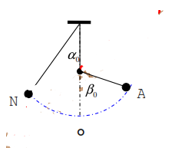
Hướng dẫn:

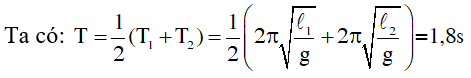
Với l₁ = 1m và l₂ = 1-0,36 = 0,64m

2.2. Thay đổi gia tốc trọng trường

• Thay đổi độ cao h, độ sâu d

• Con lắc treo trần thang máy, oto chịu tác dụng của lực quán tính

• Con lắc đơn đặt trong điện trường chịu tác dụng của lực điện

• Con lắc dơn chịu tác dụng của lực đẩy Acsimet

1. Phương pháp

♦ Thay đổi độ cao h

• Gia tốc trọng trường ở mặt đất:

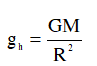
• Gia tốc trọng trường ở độ cao h:

: đưa con lắc lên cao thì gia tốc trọng trường giảm nên chu kỳ tăng

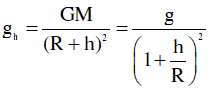
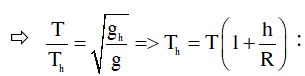
♦ Thay đổi độ sâu d

• Tương tự với thay đổi độ cao h, ta có:

: đưa con lắc xuống độ sâu d thì gia tốc trọng trường giảm nên chu kỳ tăng

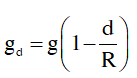
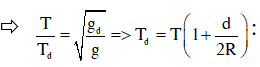
• TỔNG QUÁT: Thời gian chạy nhanh chậm của con lắc đơn trong thời gian(t) là:

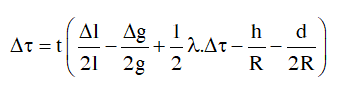
♦ Con lắc treo trần thang máy, ôtô chịu tác dụng của lực quán tính

• Thang máy chuyển động nhanh dần đều, lên trên hoặc chuyển động chậm dần đều xuống dưới ⇒ g’ = g + a : gia tốc tăng nên chu kỳ giảm

• Thang máy chuyển động nhanh dần đều xuống dưới hoặc chuyển động chậm dần đều lên trên ⇒ g’ = |g - a|: gia tốc giảm nên chu kỳ tăng

• Thang máy, oto chuyển động ngang ⇒ : gia tốc tăng nên chu kỳ giảm

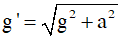
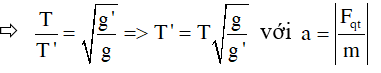
♦ Con lắc đơn đặt trong điện trường chịu tác dụng của lực điện

•Lực điện trường: F = qE , độ lớn: F = |q|E (Nếu q > 0 thì F cùng chiều E, còn q < thì F ngược chiều E)

• F cùng chiều P: g' = g + a: gia tốc tăng nên chu kì giảm

• F ngược chiều P: g' = |g - a|: gia tốc giảm nên chu kì giảm

• E có phương ngang: : gia tốc tăng nên chu kì giảm

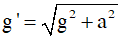
•Vị trí cân bằng mới: tanα = F/P = a/g

• Khi F kết hợp với P góc α ⇒

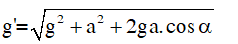
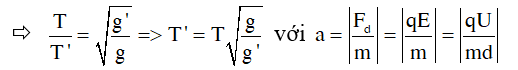
♦Con lắc đơn chịu tác dụng của lực đẩy Acsimet

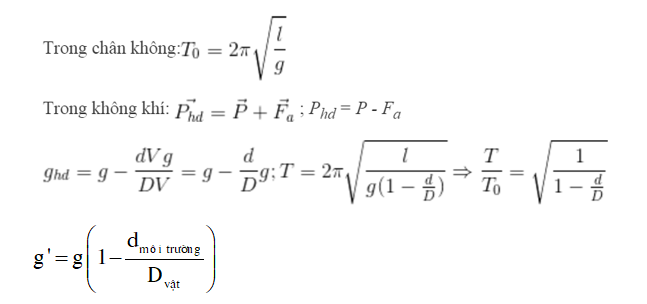
2. Ví dụ

Ví dụ 1: Một con lắc đơn treo hòn bi kim loại khối lượng m = 0,01kg mang điện tích q = 2.10^-7 C. Đặt con lắc trong điện trường đều E− có phương thẳng đứng hướng xuống dưới. Chu kỳ con lắc khi E = 0 là T = 2s. Tìm chu kỳ dao động khi E = 10⁴ V/m. Cho g = 10m/s².

A. 1,98s      B. 0,99s      C. 2,02s      D. 1,01s

Hướng dẫn:

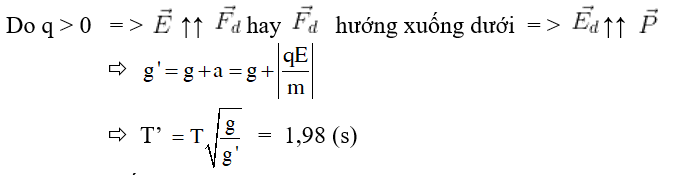
Ví dụ 2: Một con lắc đơn có chu kỳ T = 2s khi treo vào thang máy đứng yên. Khi thang máy đi lên nhanh dần đều với gia tốc 0,1m.s^-2 thì chu kỳ dao động của con lắc là

A. 2,00s      B. 2,10s      C. 1,99s      D.1,87s

Hướng dẫn:

Gia tốc hiệu dụng: g’ = g + a = 10,0 (m/s²)

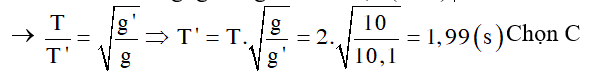
Ví dụ 3: Một con lắc đơn có chu kỳ T = 2s khi đặt trong chân không. Quả lắc làm bằng một hợp kim khối lượng riêng D = 8,67g/cm³. Tính chu kỳ T' của con lắc khi đặt con lắc trong không khí; sức cản của không khí xem như không đáng kể, quả lắc chịu tác dụng của sức đẩy Archimède, khối lượng riêng của không khí là d = 1,3g/lít.

A. 2,00024s.      B.2,00015s.      C.1,99993s.      D. 1,99985s.

Hướng dẫn:

B. Bài tập trắc nghiệm

2.1. Thay đổi chiều dài con lắc đơn

Câu 1. Một con lắc đơn dao động điều hòa,nếu giảm chiều dài con lắc đi 44 cm thì chu kì giảm đi 0,4s. Lấy g = 10 m/s²; π² = 10, coi rằng chiều dài con lắc đơn đủ lớn thì chu kì dao động khi chưa giảm chiều dài là

A. 1 s     B. 2,4 s     C. 2 s     D.1,8 s

Lời giải:

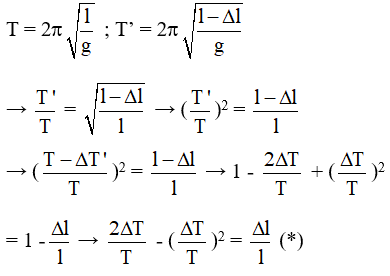
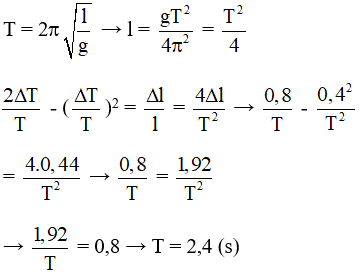
Chọn B

Câu 2. Một con lắc đơn đếm giây có chu kì bằng 2s, ở nhiệt độ 20°C và tại nơi có gia tốc trọng trường 9,813 m/s², thanh treo có hệ số nở dài là 17.10^-6K^-1. Đưa con lắc đến nơi có gia tốc trọng trường là 9,809 m/s² và nhiệt độ 30°C thì chu kì dao động là :

A. ≈ 2,0007 (s)     B. ≈ 2,0232 (s)

C. ≈ 2,0132 (s)     D. ≈ 2,0006 (s)

Lời giải:

Chu kì dao động của con lắc đơn:

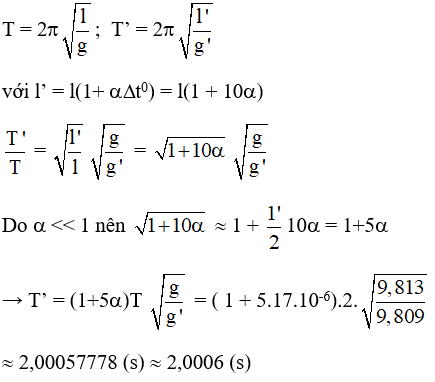
Chọn D

Câu 3. Tại cùng một địa điểm thực hiện thí nghiệm với con lắc đơn có chiều dài l₁ thì dao động với chu kỳ T₁, con lắc đơn l₂ thì dao động với chu kỳ T₂. Hỏi nếu thực hiện thực hiện thí nghiệm với con lắc đơn có chiều dài l = l₁ + l₂ thì con lắc đơn dao động với chu kỳ T là bao nhiêu?

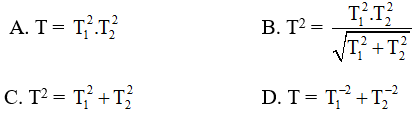
Lời giải:

Chọn C

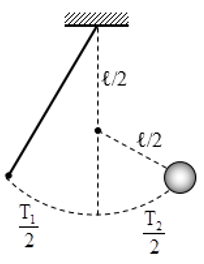
Gọi T₁ là chu kỳ của con lắc có chiều dài l₁

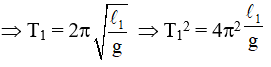
Gọi T₂ là chu kỳ của con lắc có chiều dài l₂

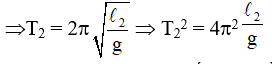
T là chu kỳ của con lắc có chiều dài l = l₁ + l₂

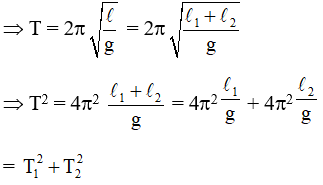
Câu 4. Ở nơi mà con lắc đơn đếm giây (chu kỳ 2s) có độ dài 1 m, thì con lắc đơn có độ dài 3 m sẽ dao động với chu kỳ là

A. T = 6 s     B. T = 4,24 s

C. T = 3,46 s     D. T = 1,5 s

Lời giải:

Chọn C. Con lắc đơn khi chiều dài là l₁ = 1 m dao động với chu kỳ

Con lắc đơn khi chiều dài là l₂ = 3 m dao động với chu kỳ

⇒

Câu 5. Một con lắc đơn có độ dài l₁ dao động với chu kỳ T₁ = 0,8 s. Một con lắc đơn khác có độ dài l₂ dao động với chu kỳ T₁ = 0,6 s. Chu kỳ của con lắc đơn có độ dài l₁ + l₂ là

A. T = 0,7 s     B. T = 0,8 s

C. T = 1,0 s     D. T = 1,4 s

Lời giải:

Chọn C. Con lắc đơn khi chiều dài là l₁ dao động với chu kỳ

Con lắc đơn khi chiều dài là l₂ dao động với chu kỳ

Con lắc đơn khi chiều dài là l₁ + l₂ dao động với chu kỳ

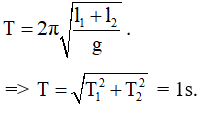
Câu 6. Tại cùng một nơi trên Trái Đất, con lắc đơn có chiều dài dao động điều hòa với chu kì 2 s, con lắc đơn có chiều dài 2 dao động điều hòa với chu kì là

A. 2 s     B. 2√2 s     C. √2 s     D. 4 s.

Lời giải:

Chọn B

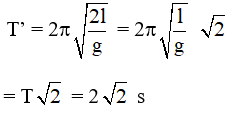
Câu 7. Tại một nơi trên mặt đất, con lắc đơn có chiều dài đang dao động điều hòa với chu kì 2 s. Khi tăng chiều dài của con lắc thêm 21 cm thì chu kì dao động điều hòa của nó là 2,2 s. Chiều dài bằng

A. 2 m     B. 1 m     C. 2,5 m     D. 1,5 m

Lời giải:

Chọn B

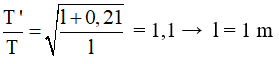
Câu 8. Hai con lắc đơn có chiều dài lần lượt là l₁ và l₂, được treo ở trần một căn phòng, dao động điều hòa với chu kì tương ứng là 2,0 s và 1,8 s. Tỷ số l₂/l₁ bằng

A. 0,81     B. 1,11     C. 1,23     D. 0,90

Lời giải:

Chọn A

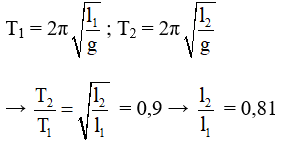
Câu 9. Tại nơi có gia tốc trọng trường g, một con lắc đơn có chiều dài l dao động điều hòa với chu kì 2,83 s. Nếu chiều dài của con lắc là 0,5 thì con lắc dao động với chu kì là

A. 1,42 s     B. 2,00 s     C. 3,14 s     D. 0,71 s

Lời giải:

Chọn B

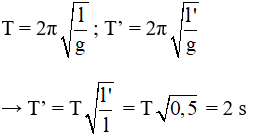
Câu 10. Tại một nơi trên mặt đất, một con lắc đơn dao động điều hòa. Trong khoảng thời gian Δt, con lắc thực hiện 60 dao động toàn phần; thay đổi chiều dài con lắc một đoạn 44 cm thì cũng trong khoảng thời gian Δt ấy, nó thực hiện 50 dao động toàn phần. Chiều dài ban đầu của con lắc là

A. 144 cm     B. 60 cm     C. 80 cm     D. 100 cm

Lời giải:

Chọn D

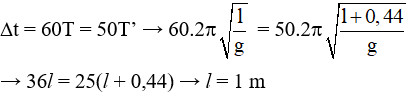
Câu 11. Tại một nơi hai con lắc đơn đang dao động điều hòa. Trong cùng một khoảng thời gian, con lắc thứ nhất thực hiện được 4 dao động, con lắc thứ hai thực hiện được 5 dao động. Tổng chiều dài của hai con lắc là 164 cm. Chiều dài của mỗi con lắc lần lượt là

A. l₁ = 100 m, l₂ = 6,4 m

B. l₁ = 64 cm, l₂ = 100 cm

C. l₁ = 1,00 m, l₂ = 64 cm

D. l₁ = 6,4 cm, l₂ = 100 cm

Lời giải:

Chọn C

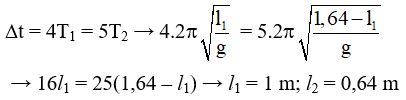
2.2. Thay đổi gia tốc trọng trường

Câu 1. Một đồng hồ quả lắc chạy đúng tại một nơi trên mặt đất. Người ta đưa đồng hồ từ mặt đất lên độ cao h = 5 km, bán kính Trái đất là R = 6400 km (coi nhiệt độ không đổi). Mỗi ngày đêm đồng hồ đó chạy

A. nhanh 68s     B. chậm 68s

C. nhanh 34s      D. chậm 34s

Lời giải:

Chọn B. Chu kỳ của con lắc khi ở mặt đất là 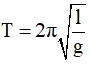, khi con lắc ở độ cao h = 5 km thì chu kỳ dao động là

Với 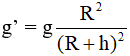suy ra g’ < g → T’ > T → đồng hồ chạy chậm. Trong mỗi ngày đêm đồng hồ chạy chậm một lượng là Δt = 24.3600(T/T' - 1), thay số ta được Δt = 68 s

Câu 2. Một con lắc lò xo đặt trên mặt phẳng ngang nhẵn, cách điện gồm vật nặng khối lượng 50g, tích điện q = 20 μC và lò xo có độ cứng k = 20 N/m. Khi vật đang nằm cân bằng thì người ta tạo một điện trường đều E = 10⁵ V/m trong không gian bao quanh con lắc có hướng dọc theo trục lò xo trong khoảng thời gian nhỏ Δt = 0,01 s và coi rằng trong thời gian này vật chưa kịp dịch chuyển. Sau đó con lắc dao động với biên độ là

A.10 cm      B. 1 cm     C.2 cm      D.20 cm

Lời giải:

Chọn D

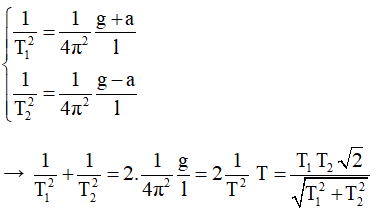
Khi có điện trường vật chịu tác dụng của lực điện trường: F = Eq. Lực F gây ra xung của lực trong thời gian Δt: FΔt = ΔP = mv là độ biến thiên động lượng của vật (vì coi rằng trong thời gian này vật chưa kịp dịch chuyển.) → v = FΔt/m = EqΔt/m

Sau đó con lắc dao động với biên độ A,

Câu 3. Con lắc đơn có vật nhỏ tích điện âm dao động điều hòa trong điện trường đều có véctơ cường độ điện trường thẳng đứng. Độ lớn lực điện tác dụng lên vật nhỏ bằng một phần tư trọng lượng của nó. Khi điện trường hướng xuống chu kỳ dao động bé của con lắc là T₁. Khi điện trường hướng lên thì chu kỳ dao động bé của con lắc là T₂. Liên hệ đúng là

A. 2T₁ = √3T₂      B. √3T₁ = √5T₂

C. √3T₂ = √5T₁     D. 2T₁ = √5T₂

Lời giải:

Chọn B. Ta có lực điện F = P/4 = mg/4.

Gia tốc biểu kiến:

+ khi điện trường hướng xuống:

+ khi điện trường hướng lên:

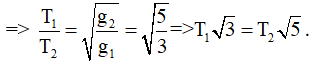
Câu 4. Một con lắc đơn có chiều dài l = 1 m treo ở trần một thang máy, khi thang máy đi xuống nhanh dần đều với gia tốc a = g/2 (g = π² m/s²) thì chu kỳ dao động bé của con lắc là

A.4 s     B. 2,83 s     C.1,64 s     D.2 s

Lời giải:

Chọn B

Khi thang máy chuyển động nhanh dần đều thì a→ cùng chiều chuyển động (hướng xuống) mà F→ ngược chiều a→ ⇒ F→ hướng lên ⇒ F→ ↓↑ P→

Gia tốc hiệu dụng

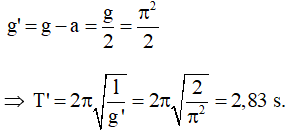
Câu 5. Một con lắc đơn có chu kỳ T = 2s khi đặt trong chân không. Quả lắc làm bằng một hợp kim khối lượng riêng D = 8,67 g/cm³. Tính chu kỳ T' của con lắc khi đặt con lắc trong không khí; sức cản của không khí xem như không đáng kể, quả lắc chịu tác dụng của sức đẩy Archimède, khối lượng riêng của không khí là D₀ = 1,3 g/lít.

A. 2,00024 s     B. 2,00015 s

C. 1,99993 s     D. 1,99985 s

Lời giải:

Chọn B. Lực đẩy Acsimet: F_p→ = -ρVg→ ( ρ = D₀ là khối lượng riêng của chất lỏng hoặc chất khí (ở đây là không khí), V là thể tích bị vật chiếm chỗ ), lực đẩy Acsimet luôn có phương thẳng đứng, hướng lên trên :

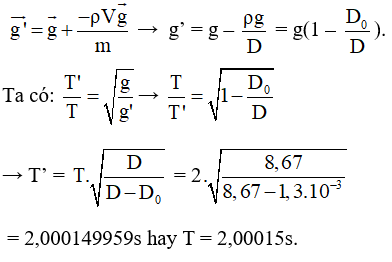
Câu 6. Treo con lắc đơn vào trần một ôtô tại nơi có gia tốc trọng trường g = 9,8 m/s². Khi ôtô đứng yên thì chu kì dao động điều hòa của con lắc là 2 s. Nếu ôtô chuyển động thẳng nhanh dần đều trên đường nằm ngang với giá tốc 2 m/s² thì chu kì dao động điều hòa của con lắc xấp xỉ bằng

A. 2,02 s     B. 1,82 s     C. 1,98 s     D. 2,00 s

Lời giải:

Chọn C

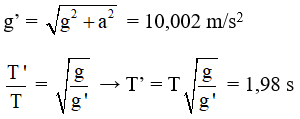
Câu 7. Một con lắc đơn có chiều dài dây treo 50 cm và vật nhỏ có khối lượng 0,01 kg mang điện tích +5.10^-6 C, được coi là điện tích điểm. Con lắc dao động điều hòa trong điện trường đều mà vectơ cường độ điện trường có độ lớn E = 10⁴ V/m, hướng thẳng đứng xuống dưới. Lấy g = 10 m/s², π = 3,14. Chu kì dao động của con lắc là

A. 0,58 s     B. 1,99 s     C. 1,40 s     D. 1,15 s

Lời giải:

q > 0 nên F→ cùng chiều với E→, a→ cùng chiều với F→ (cùng chiều với g→ ) và có độ lớn a = qE/m = 5 m/s²; g’ = g + a = 15 m/s²

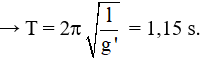
Chọn D

Câu 8. Một con lắc đơn được treo vào trần một thang máy. Khi thang máy chuyển động thẳng đứng đi lên nhanh dần đều với gia tốc có độ lớn a thì chu kì dao động điều hòa của con lắc là 2,52 s. Khi thang máy chuyển động thẳng đứng đi lên chậm dần đều với gia tốc cũng có độ lớn a thì chu kì dao động điều hòa của con lắc là 3,15 s. Khi thang máy đứng yên thì chu kì dao động điều hòa của con lắc là

A. 2,96 s     B. 2,84 s     C. 2,61 s     D. 2,78 s

Lời giải:

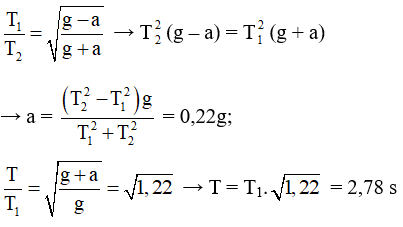
Chọn D

Câu 9. Một con lắc đơn gồm dây treo có chiều dài 1 m và vật nhỏ có khối lượng 100 g mang điện tích 2.10^-5 C. Treo con lắc đơn này trong điện trường đều với vectơ cường độ điện trường hướng theo phương ngang và có độ lớn 5.10⁴ V/m. Trong mặt phẳng thẳng đứng đi qua điểm treo và song song với vectơ cường độ điện trường, kéo vật nhỏ theo chiều của vectơ cường độ điện trường sao cho dây treo hợp với vectơ gia tốc trong trường g một góc 54° rồi buông nhẹ cho con lắc dao động điều hòa. Lấy g = 10 m/s². Trong quá trình dao động, tốc độ cực đại của vật nhỏ là

A. 0,59 m/s     B. 3,41 m/s

C. 2,87 m/s     D. 0,50 m/s

Lời giải:

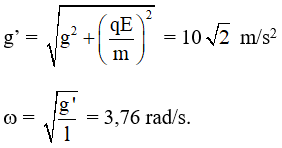
Ở vị trí cân bằng dây treo lệch so với phương thẳng đứng góc β với tanβ = qE/mg = 1 = tan45° → β = 45° → biên độ góc của dao động là α₀ = 54° – 45° = 9° = 0,157 rad; v_max = ωα₀ = 0,59 m/s. Chọn A

Câu 10. Một con lắc đơn được treo vào trần một thang máy. Khi thang máy đứng yên, con lắc dao động điều hòa với chu kỳ T. Khi thang máy đi lên thẳng đứng, chậm dần đều với gia tốc có độ lớn bằng một nửa gia tốc trọng trường tại nơi đặt thang máy thì con lắc dao động với chu kỳ T’ bằng

A. 2T     B. T/2     C. T√2      D. T/√2 .

Lời giải:

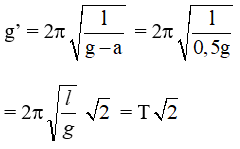
Chọn C

Cách giải bài toán Con lắc trùng phùng

A. Phương pháp & Ví dụ

1. Phương pháp

♦ Một con lắc đơn A có chu kì T dao động trước mặt một con lắc đồng hồ gõ giây B (chu kì T’ = 2s). Khi hai con lắc cùng đi qua vị trí cân bằng theo cùng một chiều ta bảo hai con lắc trùng phùng. Gọi Δt là thời gian ngăn cách giữa hai lần trùng phùng liên tiếp.

Số dao động mà con lắc B làm được trong thời gian Δt là

Δt = N.T’ = 2N → N = Δt/2

• Nếu T rất gần và nhỏ hơn T’ thì tổng thời gian Δt con lắc A sẽ làm được N + 1 dao động.

• nếu T rất gần và lớn hơn T’ thì trong khoảng thời gian Δt con lắc A sẽ làm được N – 1 dao động

⇒ Ta có hệ thức: Δt = NT’ = ( n ± 1)T

2. Ví dụ

Ví dụ 1: Một con lắc đơn A dao động trước mặt con lắc đồng hồ gõ giây B ( biết T’ = 2s). Thời gian giữa hai lần trùng phùng liên tiếp của con lắc B là 9 phút 50 giây. Tính chu kì T_A của con lắc A biết rằng chu kì cả nó lớn hơn 2 s một chút.

A. 2 s          B. 1,9932 s          C. 2,0068 s          D. 2,01 s

Hướng dẫn:

⇒ Ta có: Δt = 590s→ N_B = Δt/T_B = 590/2 = 295T_A>T_B

⇒ N_A = N_B −1 = 294

⇒ Δt = N_A .T_A = N_B .T_B

⇒ T_A = 590/294 = 2,0068s

Ví dụ 2: Cho con lắc đơn dao động trước mặt một con lắc của đồng hồ gõ giây (có chu kì dao động là 2s). Con lắc đơn dao động chậm hơn con lắc đồng hồ một chút nên có những hai lần con lắc đó chuyển động cùng chiều và đi qua vị trí cân bằng cùng một lúc ( gọi là những lần trùng phùng). Quan sát cho thấy hai lần trùng phùng kế tiếp cách nhau 9 phút 30 giây. Biết chiều dài của con lắc là l = 1m. Hãy xác định gia tốc rơi tự do g tại vị trí đặt của con lắc.

A. 9,874 m/s²          B. 9,811m/s²          C. 9,791m/s²          D. 9,654m/s²

Hướng dẫn:

Vì con lắc đơn dao động chậm hơn con lắc đồng hồ ( nghĩa là trong cùng một khoảng thời gian số dao động của nó nhỏ hơn số dao động của con lắc đồng hồ), cho nên trong khoảng thời gian Δt = 9 phút 30 giây

Vì T > 2 nên Δt = NT = (N + 1)T_o → N = Δt/T_o = ΔT/T – 1 → 1/T = 1/T_o – 1/Δt

→ T = 2,0068 s.

Gia tốc trọng trường tại nơi quan sát:

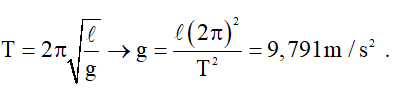
Ví dụ 3: Một con lắc lò xo và một con lắc đơn, khi ở dưới mặt đất cả hai con lắc này cùng dao động với chu kì T = 2s. Đưa cả hai con lắc lên đỉnh núi (coi là nhiệt độ không thay đổi) thì hai con lắc dao động lệch chu kì nhau. Thỉnh thoảng chúng lại cùng đi qua vị trí cân bằng và chuyển động về cùng một phía, thời gian giữa hai lần liên tiếp như vậy là 8 phút 20 giây. Tìm chu kì con lắc đơn tại đỉnh núi đó.

A. 2,010s.          B. 1,992s.          C. 2,008s.          D. 1,008 s.

Hướng dẫn:

Ta biết rằng chu kì dao động của con lắc lò xo phụ thuộc vào m và k chứ không phụ thuộc vào vị trí đặt con lắc, nên khi đưa con lắc từ mặt đất lên đỉnh núi thì chu kì dao động của con lắc lò xo không đổi và chỉ có con lắc đơn là thay đổi.

- Khi đưa con lắc đơn lên đỉnh núi thì chu kì dao động tăng, nghĩa là T > 2 s

- Δt = NT = (N+1)T_o → N = ΔtT = ΔtT_o – 1

→1/T = 1/T_o−1/Δt → T = 2,008s

→ Chọn C.

B. Bài tập trắc nghiệm

Câu 1. Dùng các chớp sáng tuần hoàn chu kỳ 2 s để chiếu sáng một con lắc đơn đang dao động. Ta thấy, con lắc dao động biểu kiến với chu kỳ 30 phút với chiều dao động biểu kiến cùng chiều dao động thật. Chu kỳ dao động thật của con lắc là:

A. 2,005 s     B. 1,978 s      C. 2,001 s     D. 1,998 s

Lời giải:

Chu kì dao đông biểu kiến chính là thời gian “trùng phùng” của hai dao động:

t = nT = (n + 1)T_thật

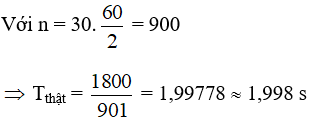
Chọn D

Câu 2. Một con lắc đơn có chu kì dao động T chưa biết dao động trước mặt một con lắc đồng hồ có chu kì T₀ = 2 s. Con lắc đơn dao động chậm hơn con lắc đồng hồ một chút nên có những lần hai con lắc chuyển động cùng chiều và trùng nhau tại vị trí cân bằng của chúng (gọi là những lần trùng phùng). Quan sát cho thấy khoảng thời gian giữa hai lần trùng phùng liên tiếp bằng 7 phút 30 giây. Hãy tính chu kì T của con lắc đơn và độ dài con lắc đơn. Lấy g = 9,8 m/s²

A. 1,98 s và 1 m

B. 2,009 s và 1 m

C. 2,009 s và 2 m

D. 1,98 s và 2 m

Lời giải:

Đối với bài toán con lắc trùng phùng ta có khoảng thời gian giữa 2 lần trùng phùng liên tiếp: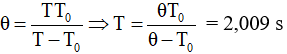, suy ra chiều dài l = 1 m. Chọn B.

Câu 3. Con lắc đơn chu kì T hơi lớn hơn 2s dao động song song trước 1 con lắc đơn gõ giây chu kỳ T₀ = 2s. Thời gian giữa 2 lần trùng phùng thứ nhất và thứ 5 là 28 phút 40 giây. Chu kì T là:

A. 2,015 s     B. 2,009 s     C. 1,995 s      D. 1,002 s

Lời giải:

Cách giải 1:

Thời gian trùng phùng của hai con lắc t = (1/4)(28 phút 40s) = (1/4).1720s = 430 s

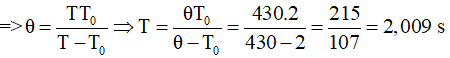
Cách giải 2:

Ta có:

(n + 1)T₀ = nT = 430 ⇒ n = 430/2 – 1 = 214 ⇒ T = 430/n = 430/214 = 2,009 s. Chọn B.

Câu 4. Hai con lắc đơn có cùng khối lượng vật nặng, dao động trong hai mặt phẳng song song cạnh nhau và cùng vị trí cân bằng. Chu kì dao động của con lắc thứ nhất bằng hai lần chu kì dao động của con lắc thứ hai và biên độ dao động của con lắc thứ hai bằng ba lần con lắc thứ nhất. Khi hai con lắc gặp nhau thì con lắc thứ nhất có động năng bằng ba lần thế năng. Tỉ số độ lớn vân tốc của con lắc thứ hai và con lắc thứ nhất khi chúng gặp nhau bằng

A. 4     B. √(14/3)     C. √(140/3)     D. 8

Lời giải:

Coi dao động của các con lắc có biên độ nhỏ: A₁ = l₁.α₁ ; A₂ = l₂.α₂

Do chu kì dao động của con lắc thứ nhất bằng hai lần chu kì dao động của con lắc thứ hai: l₁ = 4.l₂

Do biên độ dao động của con lắc thứ hai bằng ba lần con lắc thứ nhất. A₂ = 3A₁

Hay ta có: l₂.α₂ = 3l₁.α₁ Suy ra α₂ = 12.α₁

Cơ năng dao động của vật 1: E₁ = mgl₁(α₁²)/2

Khi động năng bằng 3 lần thế năng ta có:

E_đ1 = 3/4 E₁ = 3/4 mgl₁.(α₁²)/2 = 3/8 mgl₁.α₁² và li độ góc α = α₁/2

Hai vật gặp nhau ở li độ: S = l₁.α = l₁.α₁/2

Cơ năng dao động của vật 2:

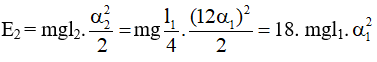
Khi hai vật gặp nhau thế năng vật 2:

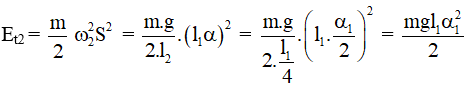
Động năng của vật 2:

E_đ2 = E₂ - E_t2 =

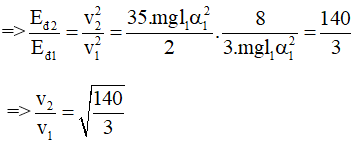
Chọn C

Câu 5. Hai con lắc đơn có chiều dài l₁ = 64 cm; l₂ = 81 cm dao động nhỏ trong hai mặt phẳng song song. Hai con lắc cùng qua vị trí cân bằng và cùng chiều t₀ = 0. Sau thời gian t ngắn nhất hai con lắc trùng phùng (cùng qua vị trí cân bằng, chuyển động cùng chiều). Lấy g = π² (m/s²). Giá trị của t là:

A. 20 s     B. 12 s     C. 8 s     D. 14,4 s

Lời giải:

Hai con lắc có chiều dài l₁ và l₂ dao động với chu kỳ khác nhau, chúng sẽ trùng phùng lần đầu khi một con lắc này dao động hơn con lắc kia đúng 1 chu kỳ. Gọi t là khoảng thời gian gần nhất mà 2 con lắc trùng phùng, n₁ là số chu kỳ vật 1 thực hiện, n₂ là số chu kỳ vật 2 thực hiện. Ta có:

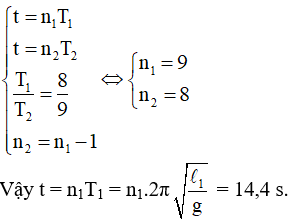
Chọn D

Câu 6. Dùng các chớp sáng tuần hoàn chu kỳ 2s để chiếu sáng một con lắc đơn đang dao động. Ta thấy, con lắc dao động biểu kiến với chu kỳ 30 phút với chiều dao động biểu kiến cùng chiều dao động thật. Chu kỳ dao động thật của con lắc là:

A. 2,005s      B. 1,978s     C. 2,001s      D. 1,998s

Lời giải:

Chu kì dao đông biểu kiến chính là thời gian “trùng phùng” của hai dao động

t = nT = (n+1) T_thật Với n = 30.60/2 = 900 thì T_thật = 1800/901 = 1,99778. Chọn D

Câu 7. Con lắc thứ nhất có chu kỳ T₁ = 3 s, con lắc thứ 2 có chu kỳ T₂. Hai con lắc trùng phùng lần thứ nhất cách nhau 99 s. Tính chu kỳ T₂.

A. 99/34 s     B. 100/33 s

C. 99/31 s     D. 49/24 s

Lời giải:

Hai con lắc trùng phùng lần thứ nhất cách nhau 100 s tức chu kỳ trùng phùng là 100 s.

Ta có: