Các dạng bài tập Con lắc lò xo có lời giải - Vật Lí lớp 12

Các dạng bài tập Con lắc lò xo có lời giải

Với Các dạng bài tập Con lắc lò xo có lời giải Vật Lí lớp 12 tổng hợp các dạng bài tập, 150 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Con lắc lò xo từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

• Lý thuyết Con lắc lò xo Xem chi tiết
• Bài tập Con lắc lò xo trong đề thi Đại học có giải chi tiết Xem chi tiết

• Dạng 1: Tính chu kì, tần số của Con lắc lò xo

  Xem chi tiết

• Dạng 2: Tính chiều dài con lắc lò xo, Lực đàn hồi, Lực phục hồi

  Xem chi tiết

• Dạng 3: Tính năng lượng của Con lắc lò xo

  Xem chi tiết

• Dạng 4: Viết phương trình dao động của Con lắc lò xo

  Xem chi tiết

3 dạng bài toán liên quan đến hai vật trong con lắc lò xo hay và khó

• Liên kết giữa hai vật khi dao động theo phương ngang (Bài tập Con lắc lò xo hay và khó) Xem chi tiết
• Liên kết giữa hai vật khi dao động theo phương thẳng đứng (Bài tập Con lắc lò xo hay và khó) Xem chi tiết
• Khoảng cách hai vật trong dao động con lắc lò xo hay và khó Xem chi tiết

Bài toán va chạm trong con lắc lò xo hay và khó

• Bài toán va chạm theo phương ngang trong con lắc lò xo hay và khó Xem chi tiết
• Bài toán va chạm theo phương thẳng đứng trong con lắc lò xo hay và khó Xem chi tiết
• Bài toán kích thích Con lắc lò xo dao động bằng ngoại lực hay và khó Xem chi tiết

Bài tập Con lắc lò xo tổng hợp

• 60 Bài tập trắc nghiệm Con lắc lò xo có lời giải

  Xem chi tiết

Cách tính chu kì, tần số của Con lắc lò xo

Loại 1: Sử dụng công thức cơ bản

A. Phương pháp & Ví dụ

1.Phương pháp

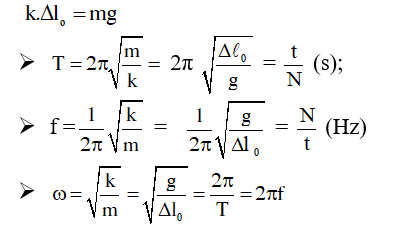
2. Ví dụ

Ví dụ 1: Một con lắc lò xo nằm ngang có độ cứng K = 100 N/m được gắn vào vật nặng có khối lượng m = 0,1kg. Kích thích cho vật dao động điều hòa, xác định chu kỳ của con lắc lò xo? Lấy π² = 10.

A. 0,1s          B. 5s          C. 2s          D. 0,3s.

Hướng dẫn:

Ta có:

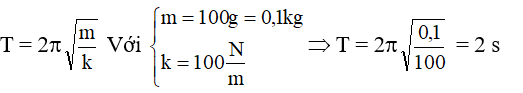
Ví dụ 2: Một con lắc lò xo có khối lượng không đáng kể, độ cứng là K, lò xo treo thẳng đứng, bên dưới treo vật nặng có khối lượng m. Ta thấy ở vị trí cân bằng lò xo giãn ra một đoạn 16cm. Kích thích cho vật dao động điều hòa. Xác định tần số của con lắc lò xo. Cho g = π²(m/s²)

A. 2,5Hz          B. 5Hz         C. 3Hz          D. 1,25Hz

Hướng dẫn:

Ta có:

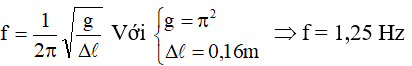
Ví dụ 3: Một con lắc lò xo có độ cứng là K, Một đầu gắn cố định, một đầu gắn với vật nặng có khối lượng m. Kích thích cho vật dao động, nó dao động điều hòa với chu kỳ là T. Hỏi nếu tăng gấp đôi khối lượng của vật và giảm độ cứng đi 2 lần thì chu kỳ của con lắc lò xo sẽ thay đổi như thế nào?

A. Không đổi          B. Tăng lên 2 lần

C. Giảm đi 2 lần          D. Giảm 4 lần

Hướng dẫn:

Gọi chu kỳ ban đầu của con lắc lò xo là:

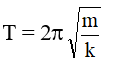
Goị T’ là chu kỳ của con lắc sau khi thay đổi khối lượng và độ cứng của lò xo.

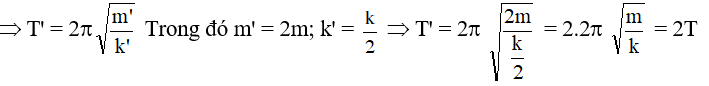
Loại 2. Bài toán ghép vật

1.Phương pháp

Bài mẫu 1: Lò xo K gắn vật nặng m1 thì dao động với chu kỳ T1. Còn khi gắn vật nặng m2 thì dao động với chu kỳ T2

Xác định chu kỳ dao động của vật khi gắn vật có khối lượng m = m₁ + m₂

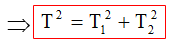
Xác định chu kỳ dao động của vật khi gắn vật có khối lượng m = m₁ + m₂ +....+ m_n

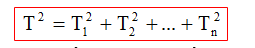
Xác định chu kỳ dao động của vật khi gắn vật có khối lượng m = a. m₁ + b.m₂:

Bài mẫu 2: Lò xo K gắn vật nặng m1 thì dao động với tần số ƒ1. Còn khi gắn vật nặng m2 thì dao động với tần số ƒ2

Xác định tần số dao động của vật khi gắn vật có khối lượng m = m₁ + m₂

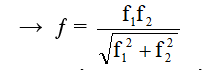
Xác định tần số dao động của vật khi gắn vật có khối lượng m = m₁ + m₂ +...+m_n

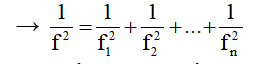
Xác định tần số dao động của vật khi gắn vật có khối lượng m = a. m₁ + b.m₂:

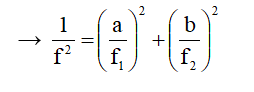
2. Ví dụ

Ví dụ 1: Một lò xo có độ cứng là K. Khi gắn vật m₁ vào lò xo và cho dao động thì chu kỳ dao động là 0,3s. Khi gắn vật có khối lượng m₂ vào lò xo trên và kích thích cho dao động thì nó dao động với chu kỳ là 0,4s. Hỏi nếu khi gắn vật có khối lượng m = 2m₁ + 3m₂ thì nó dao động với chu kỳ là bao nhiêu?

A. 0,25s B. 0,4s C. 0,812s D. 0,3s

Hướng dẫn:

Xác định chu kỳ dao động của vật khi gắn vật có khối lượng m = a. m₁ + b.m₂:

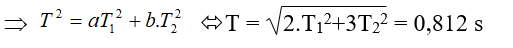
Loại 3. Bài toán cắt ghép lò xo

1.Phương pháp

a. Cắt lò xo

- Cho lò xo ko có độ dài l_o, cắt lò xo làm n đoạn, tìm độ cứng của mỗi đoạn. Ta có công thức tổng quát sau:

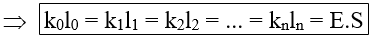
Nhận xét: Lò xo có độ dài tăng bao nhiêu lần thì độ cứng giảm đi bấy nhiêu lần và ngược lại.

b. Ghép lò xo

Trường hợp ghép nối tiếp:

Cho n lò xo nối tiếp nhau, có độ dài và độ cứng lần lượt: (l₁, k₁), (l₂, k₂), (l₃, k₃),...

Được một hệ lò xo (l, k), trong đó:

Hệ quả:

Một lò xo (l_o, k_o) cắt ra thành các đoạn (l₁, k₁), (l₂, k₂), (l₃, k₃),... Ta được hệ thức: l_ok_o = l₁k₁ = l₂k₂ l₃k₃ = ...

Ghép nối tiếp độ cứng giảm. Lò xo càng ngắn càng cứng, càng dài càng mềm.

Vật m gắn vào lò xo 1 có độ cứng k₁ thì dao động với chu kỳ T₁, gắn vật đó vào lò xo 2 có độ cứng k₂ thì khi gắn vật m vào 2 lò xo trên ghép nối tiếp thì T² = T₁² + T₂²

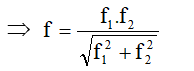
Trường hợp ghép song song

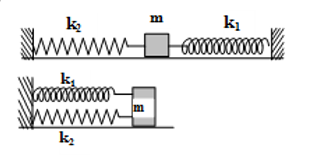
Cho 2 lò xo có độ cứng lần lượt là k₁, k₂ ghép song với nhau. Khi đó, ta được một hệ có độ cứng

Ghép song song độ cứng tăng.

Vật m gắn vào lò xo 1 có độ cứng k₁ thì dao động với chu kỳ T₁, gắn vật đó vào lò xo 2 có độ cứng k₂ thì khi gắn vật m vào 2 lò xo trên ghép song song thì

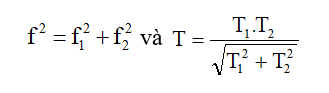
2. Ví dụ

Ví dụ 1: Một lò xo có độ dài l = 50 cm, độ cứng K = 50 N/m. Cắt lò xo làm 2 phần có chiều dài lần lượt là l1 = 20 cm, l2 = 30 cm. Tìm độ cứng của mỗi đoạn:

A. 150N/m; 83,3N/m B. 125N/m; 133,3N/m

C. 150N/m; 135,3N/m D. 125N/m; 83,33N/m

Hướng dẫn:

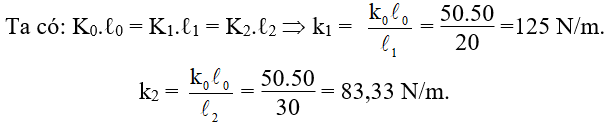
Ví dụ 2: Một lò xo có chiều dài l_o, độ cứng K_o = 100N/m. Cắt lò xo làm 3 đoạn tỉ lệ 1:2:3. Xác định độ cứng của mỗi đoạn.

A. 200; 400; 600 N/m          B. 100; 300; 500 N/m

C. 200; 300; 400 N/m          D. 200; 300; 600 N/m

Hướng dẫn:

Ta có: K_o.l_o = K₁.l₁ = K₂.l₂ = K₃.l₃

Tương tự cho k₃

Ví dụ 3: lò xo 1 có độ cứng K₁ = 400 N/m, lò xo 2 có độ cứng là K₂ = 600 N/m. Hỏi nếu ghép song song 2 lò xo thì độ cứng là bao nhiêu?

A. 600 N/m          B. 500 N/m          C. 1000 N/m          D. 2400N/m

Hướng dẫn:

Ta có: Vì lò xo ghép // K = K₁ + K₂ = 40 + 60 = 100 N/m.

Cách tính chiều dài con lắc lò xo, Lực đàn hồi, Lực phục hồi

A. Phương pháp & Ví dụ

1.Phương pháp

2.1. Chiều dài của lò xo:

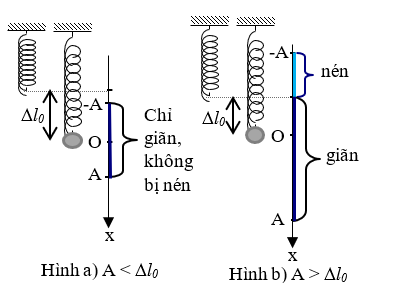
- Gọi l_o là chiều dài tự nhiên của lò xo

- l là chiều dài khi con lắc ở vị trí cân bằng: l = l_o + Δl_o

- A là biên độ của con lắc khi dao động.

- Gốc tọa độ tại vị trí cân bằng, chiều dương hướng xuống dưới.

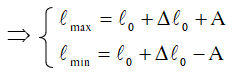
2.2. Lực đàn hồi:

F_dh = - K.Δx (N)

(Nếu xét về độ lớn của lực đàn hồi). F_dh = K.(Δl_o + x)

F_dhmax = K(Δl_o + A)

F_dhmin = K(Δl_o - A) Nếu Δl_o > A

F_dhmin = 0 khi l_o ≤ A (F_dhmin tại vị trí lò xo không bị biến dạng)

2.3. Lực phục hồi (lực kéo về):

F_ph = ma = m (- ω².x) = - K.x

Nhận xét: Trường hợp lò xo treo thẳng đứng lực đàn hồi và lực phục hồi khác nhau.

Trong trường hợp A > Δl_o

F_nén = K(|x| - Δl_o) với |x| ≥ Δl_o.

F_nenmax = K|A-Δl_o|

2.4. Bài toán: Tìm thời gian lò xo bị nén, giãn trong một chu kỳ:

Gọi φ_nén là góc nén trong một chu kỳ.

- φ_nén = 2.α Trong đó: cosα = Δl_o/A

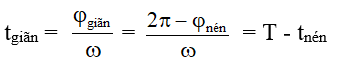
Nhận xét: t_giãn = 2t_nén, t_giãn = 3t_nén, t_giãn = 5t _nén (tỉ lệ 2:3:5) thì tương ứng với 3 vị trí đặc biệt trên trục thời gian

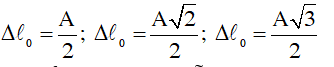
Đối với con lắc lò xo nằm ngang ta vẫn dùng các công thức của lò xo thẳng đứng nhưng Δl_o = 0 và lực phục hồi chính là lực đàn hồi F_dhmax F_hp = k.A và F_dhmin = 0

2. Ví dụ

Ví dụ 1: Một con lắc lò xo có chiều dài tự nhiên là l_o = 30 cm, độ cứng của lò xo là K = 10 N/m. Treo vật nặng có khối lượng m = 0,1 kg vào lò xo và kích thích cho lò xo dao động điều hòa theo phương thẳng đứng với biên độ A = 5 cm. Xác định chiều dài cực đại, cực tiểu của lò xo trong quá trình dao động của vật.

A. 40cm; 30 cm          B. 45cm; 25cm

C. 35 cm; 55cm          D. 45 cm; 35 cm.

Hướng dẫn:

Ta có: l_o = 30 cm và Δl_o = mg/k = 0,1 m = 10 cm

l_max = l_o + Δl_o + A = 30 + 10 +5 = 45 cm

l_min = l_o + Δl_o - A = 30 + 10 - 5 = 35 cm

Ví dụ 2: Một con lắc lò xo có chiều dài tự nhiên là l_o = 30 cm, độ cứng của lò xo là K = 10 N/m. Treo vật nặng có khối lượng m = 0,1 kg vào lò xo và kích thích cho lò xo dao động điều hòa theo phương thẳng đứng với biên độ A = 5 cm. Xác định lực đàn hồi cực đại, cực tiểu của lò xo trong quá trình dao động của vật.

A. 1,5N; 0,5N          B. 2N; 1.5N          C. 2,5N; 0,5N          D. Khác

Hướng dẫn:

Ta có: Δl_o = 0,1 m > A.

Áp dụng F_dhmax = K(A + Δl_o) = 10(0,1 + 0,05) = 1,5 N

F_dhmin = K(A - Δl_o) = 10(0,1 - 0,05) = 0,5 N

Ví dụ 3: Một con lắc lò xo có chiều dài tự nhiên là l_o = 30 cm, độ cứng của lò xo là K = 10 N/m. Treo vật nặng có khối lượng m = 0,1 kg vào lò xo và kích thích cho lò xo dao động điều hòa theo phương thẳng đứng với biên độ A = 20 cm. Xác định lực đàn hồi cực đại, cực tiểu của lò xo trong quá trình dao động của vật.

A. 1,5N; 0N         B. 2N; 0N          C. 3N; 0N          D. Khác

Hướng dẫn:

Ta có Δl_o = 0,1 m < A nên F_dhmax = K(A+ Δl_o) = 10(0,1 + 0,2) = 3 N

và F_dhmin = 0 vì Δl_o < A

Ví dụ 4: Một con lắc lò xo có chiều dài tự nhiên là l_o = 30 cm, độ cứng của lò xo là K = 10 N/m. Treo vật nặng có khối lượng m = 0,1 kg vào lò xo và kích thích cho lò xo dao động điều hòa theo phương thẳng đứng với biên độ A = 20 cm. Xác định thời gian lò xo bị nén trong một chu kỳ?

A. π/15 s          B. π/10 s          C. π/5 s          D. π s

Hướng dẫn:

Cách 1:

Ta có: t_nén = Φ/ω

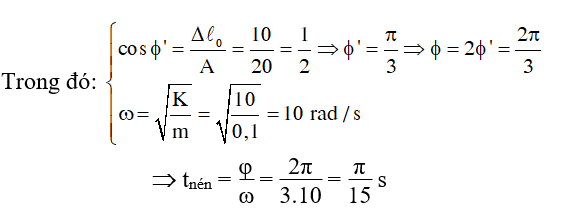
Cách 2: Sử dụng trục thời gian

Ta có: Thời gian lò xo nén 1 lần là thời gian ngắn nhất vật đi từ -Δl_o đến –A

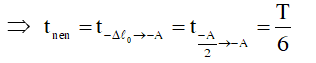
Vì trong 1T lò xo nén 2 lần nên thời gian giãn trong 1T cần tìm

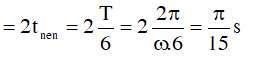
Ví dụ 5: Một con lắc lò xo có chiều dài tự nhiên là l_o = 30 cm, độ cứng của lò xo là K = 10 N/m. Treo vật nặng có khối lượng m = 0,1 kg vào lò xo và kích thích cho lò xo dao động điều hòa theo phương thẳng đứng với biên độ A = 20 cm. Xác định tỉ số thời gian lò xo bị nén và giãn.

A. 12          B. 1          C. 2          D. 14

Hướng dẫn:

Cách 1:

Gọi H là tỉ số thời gian lò xo bị nén và giãn trong một chu kỳ.

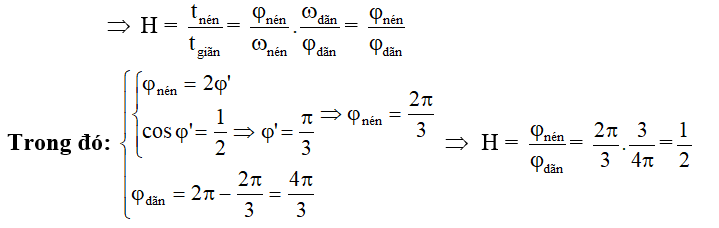
Cách 2: Sử dụng trục thời gian

Ta dễ dàng tính được

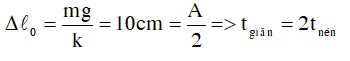
Cách viết phương trình dao động của Con lắc lò xo

A. Phương pháp & Ví dụ

1. Phương pháp

Phương trình dao động của con lắc lò xo có dạng x = Acos(ωt + Φ), tìm A, ω, Φ là ta viết được phương trình dao động của con lắc.

Sử dụng:

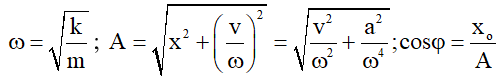
( lấy nghiệm “ – “ khi v > 0 ; lấy nghiệm “+” khi v < 0), với xo, vo là li độ và vận tốc tại thời điểm t = 0.

2. Ví dụ

Ví dụ 1: Một con lắc lò xo treo thẳng đứng gồm 1 lò xo nhẹ có độ cứng k = 40 N/m, vật năng m = 100g. Từ VTCB kéo vật xuống 1 đoạn để lò xo giãn 7,5 cm rồi buông cho vật DĐĐH. Lấy g = 10 m/s². Chọn trục tọa độ Ox trùng với trục lò xo, gốc tọa độ O tại VTCB, chiều dương hướng xuống, gốc thời gian là lúc vật qua VTCB lần đầu tiên. Viết phương trình dao động của vật?

Hướng dẫn:

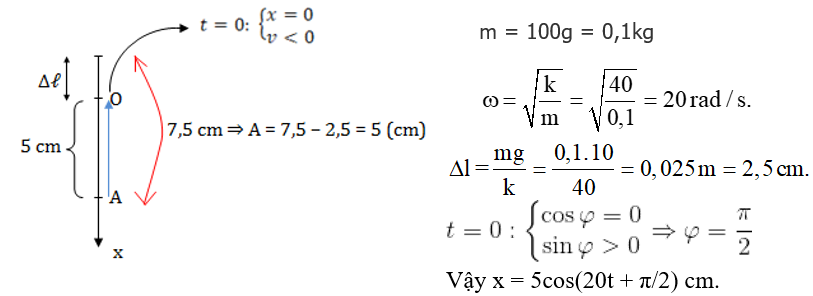
Ví dụ 2: Con lắc lò xo dao dộng điều hòa theo phương thắng đứng với tần số 4,5 Hz.Trong quá trình dao động,chiều dài lò xo biến đổi từ 4040 cm đến 56 cm. Chọn trục 0x thắng đứng hướng lên, gốc 0 tại vị trí cân bằng, lúc t = 0 lò xo dài 52 cm và vật đi ra xa vị trí cân bằng. Phương trình dao động của vật là?

Hướng dẫn:

Ta có ω = 2πf = 9π rad/s.

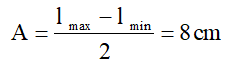
Chọn trục Ox thẳng đứng có chiều dương hướng lên, gốc tại vtcb.

Lúc t = 0, lò xo dài 52 cm và vật đi ra xa vtcb tức là vật đang ở vị trí x = -A/2 = -4 cm và chuyển động theo chiều âm → Φ = 2π/3.

→ Phương trình x = 8cos(9πt + 2π /3) cm.