Cách giải Bài tập Hai vật dao động điều hòa cùng tần số hoặc khác tần số hay, chi tiết - Vật Lí lớp 12

Cách giải Bài tập Hai vật dao động điều hòa cùng tần số hoặc khác tần số hay, chi tiết

Với Cách giải Bài tập Hai vật dao động điều hòa cùng tần số hoặc khác tần số hay, chi tiết Vật Lí lớp 12 tổng hợp ? bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Hai vật dao động điều hòa cùng tần số hoặc khác tần số từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

Câu 1. Hai chất điểm dao động điều hòa với chu kỳ T, lệch pha nhau ∆φ = π/3 với biên độ lần lượt là A và 2A, trên hai trục tọa độ song song cùng chiều, gốc tọa độ nằm trên đường vuông góc chung. Khoảng thời gian nhỏ nhất giữa hai lần chúng gặp nhau là:

A. T    B. T/2    C. T/3    D. T/4

Lời giải:

Do hai dao động cùng chu kì, nên tần số góc bằng nhau.

Giả sử tại thời điểm t₀ hai chất điểm gặp nhau, khi đó M₀N₀ vuông góc với trục Ox.

Mặt khác độ lệch pha của hai chất điểm là ∆φ = π/3 nên từ hình vẽ ta có x₁ = x₂ = A.

Sau nửa chu kì MN lại vuông góc với Ox, tức là hai chất điểm lại gặp nhau

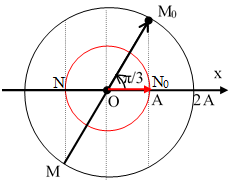
Vậy khoảng thời gian nhỏ nhất giữa hai lần chúng gặp nhau là: ∆t = T/2 .

Chọn đáp án B

Câu 2. Hai chất điểm dao động điều hòa cùng tần số trên hai đường thẳng song song kề nhau cách nhau 5 cm và song song với Ox có đồ thị li độ như hình vẽ. Vị trí cân bằng của hai chất điểm đều ở trên một đường thẳng qua gốc tọa độ và vuông góc với Ox. Biết t₂ - t₁ = 1,08 s. Kể từ lúc t = 0, hai chất điểm cách nhau 5√3 cm lần thứ 2016 là

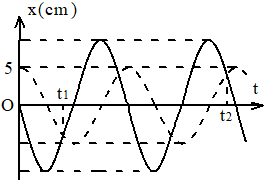
A. 362,73 s.    B. 362,85 s.

C. 362,67 s.    D. 362,70 s.

Lời giải:

Từ đồ thị ta tìm được phương trình dao động của 2 vật: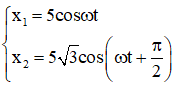

Khi đồ thị cắt nhau, tức là 2 vật cùng nằm trên một đường thẳng vuông góc với Ox, khi đó x₂ – x₁ = 0.

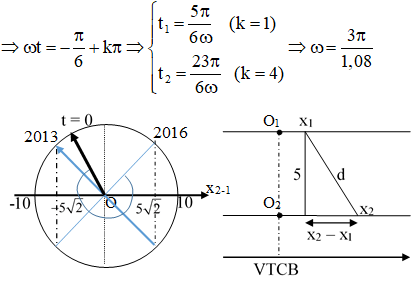
Gọi d là khoảng cách giữa 2 vật: d₂ = (x₂ – x₁)² + 5²;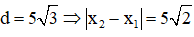

Bấm máy x_2-1 = x₂ – x₁ =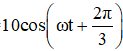

Trong một chu kỳ có 4 thời điểm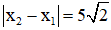

Từ vòng tròn biểu diễn hiệu x₂ – x₁ ta nhận thấy lần thứ 2016 kể từ t = 0 tương ứng với khoảng thời gian là: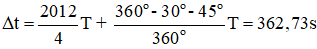

Chọn đáp án A

Câu 3. Hai chất điểm M và N dao động điều hòa cùng tần số dọc theo hai đường thẳng song song kề nhau và song song với trục tọa độ Ox. Vị trí cân bằng của M và N đều ở trên một đường thẳng qua gốc tọa độ và vuông góc với Ox. Phương trình dao động của M và N lần lượt là 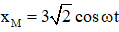(cm) và (cm). Kể từ t = 0, thời điểm M và N có vị trí ngang nhau lần thứ 3 là :

A. T    B. 9T/8    C. T/2    D. 5T/8

Lời giải:

Cách 1:

Khoảng cách giữa M và N :

x = x_N – x_M = Acos(Δt + φ) Với: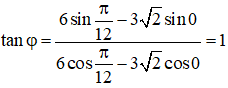

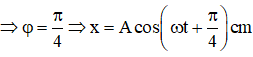
Khi M, N có VT ngang nhau:

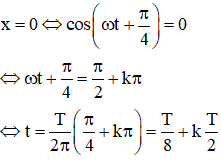
M và N có vị trí ngang nhau lần thứ 3 khi k = 2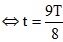

Cách 2: Tại thời điểm t = 0, hai vật không gặp nhau.

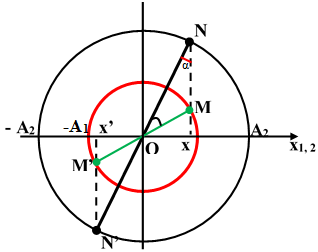
Tại thời điểm gặp nhau thì MN vuông góc với Ox. Sử dụng định lý Hàm số cosin trong tam giác MON ta tính được cạnh MN

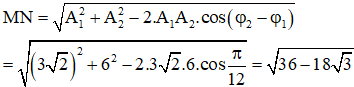
Sử dụng định lý hàm số sin (hoặc dùng định lý hàm số côsin) ta tìm được góc α

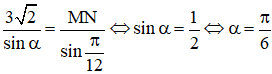
Như vậy ta tìm được pha dao động của N tại thời điểm gặp nhau:

ϕ2(t) = (π/2 – π/6) + kπ = π/3 + kπ (vì vật 2 nhanh pha hơn vật 1) với k = 0, 1, 2, 3…

Ta có: ωt + φ₂ = π/3 + kπ ↔ 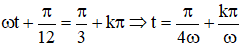(s) với k = 0, 1, 2, 3…

Lần thứ 3 gặp nhau ứng với k = 2 →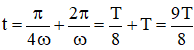

Câu 4. Hai chất điểm dao động điều hòa trên cùng một trục tọa độ Ox theo các phương trình lần lượt là x₁ = 4cos4πt cm và 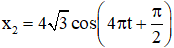cm. Thời điểm lần đầu tiên hai chất điểm gặp nhau là

A. 1/16    B. 1/4s    C. 1/12 s    D. 5/24s

Lời giải:

Biểu diễn các dao động x₁, x₂ bằng các véctơ 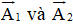tương ứng.

Chú ý: Ban đầu hai véctơ này lần lượt trùng với trục ox và oy và chúng cùng quay theo chiều dương của đường tròn lượng giác.

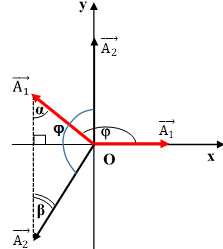
Hai dao động này vuông pha nhau và cùng tần số góc nên góc hợp bởi hai véctơ này không đổi theo thời gian. Khi hai chất điểm gặp nhau (chúng có cùng li độ) thì đoạn thẳng nối hai đầu mút của hai véctơ (cạnh huyền của tam giác vuông) phải vuông góc với trục Ox.

Ta có: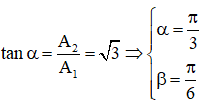

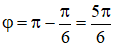
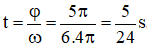
Do đó góc quét φ của hai véctơ là: . Thời điểm lần đầu tiên hai chất điểm gặp nhau là:

Chọn D.

Câu 5. Cho hai vật dao động điều hoà trên cùng một trục toạ độ Ox, có cùng vị trí cân bằng là gốc O và có cùng biên độ và với chu kì lần lượt là T₁ = 1 s và T₂ = 2 s. Tại thời điểm ban đầu, hai vật đều ở miền có gia tốc âm, cùng đi qua vị trí có động năng gấp 3 lần thế năng và cùng đi theo chiều âm của trục Ox. Thời điểm gần nhất ngay sau đó mà hai vật lại gặp nhau là

A. 2/9s    B. 4/9s    C. 2/3s    D. 1/3s

Lời giải:

Tại thời điểm ban đầu, hai vật đều ở miền có gia tốc âm nên x > 0, cùng đi qua vị trí có động năng gấp 3 lần thế năng x = A/2 và cùng đi theo chiều âm của trục Ox.

Phương trình dao động của 2 vật lần lượt là:

và

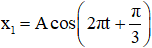
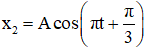
Khi hai vật gặp nhau thì:

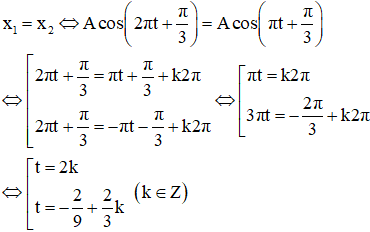
Khi k = 1 thì t = 2 và t = 4/9s. Vậy tmin = 4/9s.

Chọn đáp án B

Câu 6. Hai chất điểm M và N dao động điều hòa cùng tần số ω = 4π rad/s dọc theo hai đường thẳng song song kề nhau và song song với trục tọa độ Ox. Vị trí cân bằng của M và của N đều ở trên một đường thẳng qua gốc tọa độ và vuông góc với Ox. Trong quá trình dao động, khoảng cách lớn nhất giữa M và N theo phương Ox là 10√3 cm. Tại thời điểm t₁ hai vật cách nhau 15cm, hỏi sau khoảng thời gian ngắn nhất là bao nhiêu kể từ thời điểm t₁ khoảng cách giữa chúng bằng 15cm.

Lời giải:

Cách 1: Theo đề ta có:

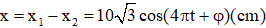
Giải sử chọn φ = 0, nghĩa là lúc t = 0: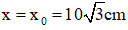

tại t₁:

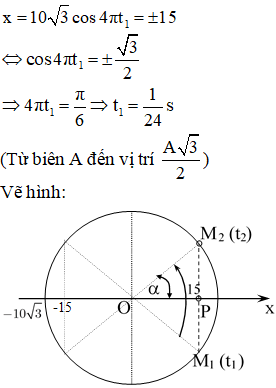
Từ hình vẽ: Dễ thấy 2 thời điểm gần nhất là 2 lần t₁ :

Từ M1 đến M2: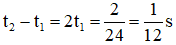

Chọn đáp án A

Cách 2: Trên hình vẽ đường tròn lượng giác:

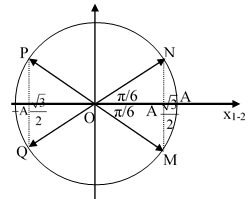
Giả sử tại M, N, P và Q là các lần mà hai vật cách nhau 15cm.

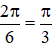
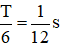
Khoảng thời gian ngắn nhất là kể từ thời điểm t₁ khoảng cách giữa chúng bằng 15cm. Hay về thời gian là .v

Chọn đáp án A

Câu 7. Hai điểm sáng 1 và 2 cùng dao động điều hòa trên trục Ox với phương trình dao động lần lượt : x₁ = A₁ cos(ω₁t + φ) cm, x₂ = A₂ cos( ω₂t + φ) cm (với A₁ < A₂, ω₁ < ω₂ và 0 < φ < π/2). Tại thời điểm ban đầu t = 0 khoảng cách giữa hai điểm sáng là a√3. Tại thời điểm t = Δt hai điểm sáng cách nhau là 2a, đồng thời chúng vuông pha. Đến thời điểm t = 2Δt thì điểm sáng 1 trở lại vị trí đầu tiên và khi đó hai điểm sáng cách nhau 3a√3. Tỉ số 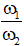bằng:

A. 4,0    B. 3,5    C. 3,0    D. 2,5

Lời giải:

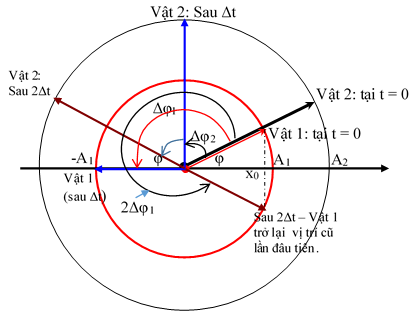
+ Tại t = 0 (2 dao động biểu diễn bằng 2 vectơ quay màu đỏ).

Khoảng cách trên Ox là A₂cosφ – A₁cosφ = a√3 (1)

+ Sau Δt (2 dao động biểu diễn bằng 2 vectơ quay màu xanh): Vật 1 quay góc Δφ₁, vật 2 quay góc Δφ₂.

Vì vật 1, sau thời gian 2Δt quay góc 2Δφ₁ thì nó trở lại vị trí cũ x0 lần đầu nên sau Δt (ứng với góc quay Δφ₁) nó phải ở -A₁ như hình vẽ.

Ở thời điểm ∆t, vật 2 chuyển động chậm hơn và vuông pha với vật 1 nên vật 2 ở vị trí như hình vẽ.

Khoảng cách 2 vật lúc này là: d = A₁ = 2a (2)

+ Sau 2Δt, vật 1 quay thêm góc Δφ₁ nữa, vật 2 quay góc Δφ₂ nữa. Chúng biểu diễn bằng các vecto màu nâu.

Khoảng cách của chúng: d’ = A₂cosφ + A₁cosφ = 3a√3 (3)

+ Giải hệ (1) (2) và (3) φ = π/6.

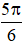
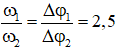
Theo hình vẽ: Δφ₁ = π - φ = , Δφ₂ = π/2 - φ = π/3. Vậy

Chọn đáp án D

Câu 8. Hai vật dao động điều hoà cùng pha ban đầu, cùng phương và cùng biên độ với các tần số góc lần lượt là: ω₁ = π/6 (rad/s); ω₂ = π/3 (rad/s). Chọn gốc thời gian lúc hai vật đi qua vị trí cân bằng theo chiều dương. Thời gian ngắn nhất mà hai vật gặp nhau là:

A. 1s    B. 4s.    C. 2s.    D. 8s

Lời giải:

Phương trình dao động của hai vât:

x₁ = A₁cos(ω₁t – π/2); x₂ = A₂cos(ω₂t – π/2).

Hai vật gặp nhau lần đầu khi pha của chúng đối nhau: (ω₁t - π/2) = - (ω₂t - π/2)

(ω₁ + ω₂ ).t = π → t = π/(ω₁ + ω₂ ) = 2s.

Chọn đáp án C

Câu 9. Hai chất điểm dao động điều hoà trên hai trục tọa độ Ox và Oy vuông góc với nhau (O là vị trí cần bằng của cả hai chất điểm). Biết phương trình dao động của hai chất điểm là: x = 2cos(5πt +π/2) cm và y = 4cos(5πt – π/6) cm. Khi chất điểm thứ nhất có li độ x = cm và đang đi theo chiều âm thì khoảng cách giữa hai chất điểm là

Lời giải:

Ta có: t = 0:

x = 0, v_x < 0 chất điểm qua VTCB theo chiều âm.

y = 2√3, v_y > 0, chất điểm y đi từ 2√3 ra biên.

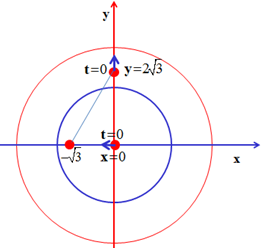
* Khi chất điểm x đi từ VTCB đến vị trí x = -√3 cm hết thời gian T/6

* Trong thời gian T/6 đó, chất điểm y đi từ y = 2√3, ra biên dương rồi về lại đúng y = 2√3,

* Vị trí của 2 vật như hình vẽ.

Khoảng cách giữa 2 vật là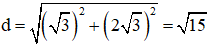

Chọn D

Câu 10. Hai chất điểm P và Q dao động điều hòa trên cùng một trục Ox (trên hai đường thẳng song song kề sát nhau) với phương trình lần lượt là x₁ = 4cos(4πt + /3) (cm) và x₂ = 4 cos(4πt + π/12) (cm). Coi quá trình dao động hai chất điểm không va chạm vào nhau. Hãy xác định trong quá trình dao động khoảng cách lớn nhất và nhỏ nhất giữa hai chất điểm là bao nhiêu?

A. d_min = 0(cm); d_max = 8(cm)

B. d_min = 2(cm); d_max = 8(cm)

C. d_min = 2(cm); d_max = 4(cm)

D. d_min = 0(cm); d_max = 4(cm)

Lời giải:

Để xác định khoảng cách ta viết phương trình hiệu của x₁ và x₂:

d = x = x₁ – x₂ = Acos(ωt + φ)

Trong đó: A² = A₁² + A₂² – 2A₁A₂cos(φ1 - φ2) = 4² ⇒ A = 4cm

⇒ d_min = x_min = 0(cm); d_max = x_max = 4(cm)

Chọn D.