Công thức, cách giải bài tập Tổng hợp dao động điều hòa hay, chi tiết - Vật Lí lớp 12

Công thức, cách giải bài tập Tổng hợp dao động điều hòa hay, chi tiết

Với Công thức, cách giải bài tập Tổng hợp dao động điều hòa hay, chi tiết Vật Lí lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập dao động điều hòa từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

A. Phương pháp & Ví dụ

1. Biểu diễn dao động điều hòa bằng véc-tơ quay

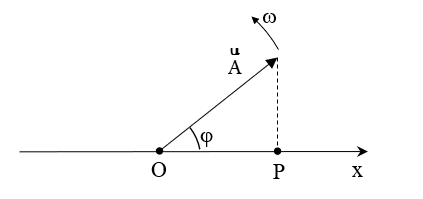
Xét một véc tơ quay ngược chiều kim đồng hồ quanh gốc O, có đặc điểm:

• Độ dài vec tơ bằng A.

• Tốc độ quay ω.

• Ban đầu hợp với trục Ox góc φ.

Khi đó, hình chiếu P của ngọn véc tơ xuống trục Ox biểu diễn một dao động điều hòa x = Acos(ωt + φ).

2. Tổng hợp 2 dao động điều hòa cùng phương, cùng tần số

Khi vật tham gia đồng thời nhiều dao động cùng tần số thì dao động của vật là dao động tổng hợp. Giả sử một vật tham gia đồng thời hai dao động :

x₁ = A1cos(ωt + φ₁)

x₂ = A2cos(ωt + φ₂)

Khi đó dao động tổng hợp có dạng x = Acos(ωt + φ). Hai cách tính :

• Nếu cùng biên độ thì cộng lượng giác x = x₁ + x₂ (ít gặp).

• Nếu biên độ khác nhau thì nên sử dụng biểu diễn véc tơ quay để tổng hợp các dao động điều hòa cùng phương cùng tần số:

Phương pháp véc tơ quay:

A² = A₁² + A₂² + 2A₁A₂cos(φ₂ – φ₁)

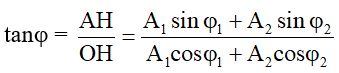
Nếu véc tơ :

• Cùng pha ⇒A_max = A₁ + A₂, φ = φ₁ = φ₂.

• Ngược pha ⇒A_min = |A₁ – A₂|. Nếu A₁ > A₂ ⇒φ = φ₁; nếu A₁ < A₂ ⇒ φ = φ₂.

• Vuông pha ⇒ A² = A₁² + A₂².

• Khi A₁ và A₂ xác định, φ₁ và φ₂ chưa biết, ta luôn có |A₁ – A₂| ≤ A ≤ |A₁ + A₂|

3. Sử dụng máy tính giải bài toán tổng hợp phương trình dao động

4. Ví dụ

Ví dụ 1: Một vật thực hiện đồng thời 2 dao động điều hòa x₁ = 3cos(4πt + π/6) cm và x₂ = 3cos(4πt + π/2) cm. Hãy xác định dao động tổng hợp của hai dao động trên?

A. x = 3√3cos(4πt + π/6) cm          B. x = 3√3cos(4πt + π/3) cm

C. x = 3√3cos(4πt + π/3) cm          D. x = 3cos(4πt + π/3) cm

Hướng dẫn:

Ta có: dao động tổng hợp có dạng: x = Acos(ωt + φ) cm

Trong đó:

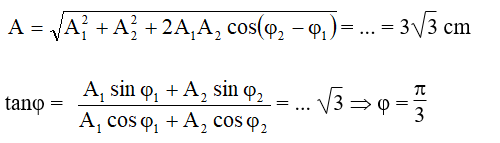
Phương trình dao động cần tìm là x = 3√3cos(4πt + π/3) cm

Ví dụ 2: Một vật thực hiện đồng thời 2 dao động điều hòa với biên độ lần lượt là 3 cm và 5 cm. Trong các giá trị sau giá trị nào không thể là biên độ của dao động tổng hợp.

A. 4 cm          B. 5 cm         C. 3cm          D. 10 cm

Hướng dẫn:

Ta có: |A₁ - A₂ | ≤ A ≤ A₁ + A₂

⇒ 2 cm ≤ A ≤ 8 cm

Ví dụ 3: Một vật thực hiện hai dao động điều hòa với phương trình lần lượt là x₁ = 4cos(6πt + π/3); x₂ = cos(6πt + π) cm. Hãy xác định vận tốc cực đại mà dao động có thể đạt được.

A. 54π cm/s          B. 6π cm/s          C. 45cm/s          D. 9π cm/s

Hướng dẫn:

Ta có: V_max = A.ω ⇒ V_max khi A_max Với A_max = 9 cm khi hai dao động cùng pha

⇒ V_max = 9.6π = 54π cm/s.

Ví dụ 4: Một chất điểm dao động điều hoà có phương trình dao động tổng hợp x = 5√2 cos(πt + 5π/12) với các dao động thành phần cùng phương, cùng tần số là x₁ = A₁ cos(πt + π1) và x₂ = 5cos(πt + π/6 ), pha ban đầu của dao động 1 là:

A. φ₁ = 2π/3          B. φ₁= π/2          C.φ₁ = π/4          D. φ₁= π/3

Hướng dẫn:

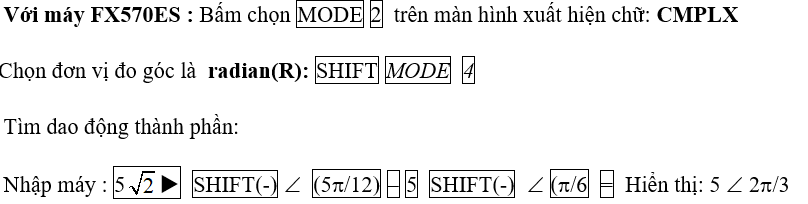
B. Bài tập trắc nghiệm

Câu 1. Cho hai dao động điều hoà cùng phương có phương trình dao động lần lượt là x₁ = 3√3sin(5πt + π/2)(cm) và x₂ = 3√3sin(5πt - π/2)(cm). Biên độ dao động tổng hợp của hai dao động trên bằng

A. 0 cm     B. 3 cm     C. 63 cm     D. 33 cm

Lời giải:

Hai dao động trên ngược pha nhau vì Δφ = φ₂-φ₁ = -π nên biên độ dao động tổng hợp sẽ là: A = |A₂ - A₁| = 0.

Câu 2. Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là x₁ = 3cos10t (cm) và x₂ = 4sin(10t + π/2)(cm). Gia tốc của vật có độ lớn cực đại bằng

A. 7 m/s²     B. 3 m/s²     C. 6 m/s²     D. 13 m/s²

Lời giải:

Đưa phương trình li độ của dao động thứ 2 về dạng chuẩn theo cos: x₂ = 4sin(10t + π/2) = 4cos(10t)

Từ đây ta thấy rằng: hai dao động trên cùng pha vì thế biên độ dao động tổng hợp: A = A₁ + A₂ = 3 + 4 = 7 (cm)

Gia tốc có độ lớn cực đại: a_max = ω²A = 100.7 = 700 cm/s² = 7 m/s²

Câu 3. Dao động của một chất điểm có khối lượng 100 g là tổng hợp của hai dao động điều hòa cùng phương, có phương trình li độ lần lượt là x₁ = 5cos(10t) và x₂ = 10cos(10t) (x₁ và x₂ tính bằng cm, t tính bằng s). Mốc thế năng ở vị trí cân bằng. Cơ năng của chất điểm bằng

A. 0,1125 J     B. 225 J     C. 112,5 J     D. 0,225 J

Lời giải:

Hai dao động trên cùng pha vì thế biên độ dao động tổng hợp: A = A₁ + A₂ = 5 + 10 = 15 cm

Cơ năng của chất điểm: E = (1/2).m.ω²A² = (1/2). 0,1. 10².0,15² = 0,1125 J

Câu 4. Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là x₁ = 4cos(10t + π/4)(cm) và x₂ = 3cos(10t - 3π/4)(cm). Độ lớn vận tốc của vật ở vị trí cân bằng là

A. 100 cm/s     B. 50 cm/s

C. 80 cm/s     D. 10 cm/s

Lời giải:

Ta có: Δφ = φ₂-φ₁ = (-3π/4)-π/4 = -π ⇒ hai dao động trên ngược pha

Biên độ dao động tổng hợp: A = |A₁ - A₂| = 1 cm

Vận tốc của ở VTCB là: v_VTCB = v_max = ωA = 10.1 = 10 cm/s . Chọn D

Câu 5. Dao động của một vật là tổng hợp của hai dao động cùng phương có phương trình lần lượt là x₁ = Acosωt và x₂ = Asinωt. Biên độ dao động của vật là

A. √3A     B. A     C. √2A     D. 2A

Lời giải:

Chuyển phương trình của thành phần thứ 2 về dạng chuẩn theo cos: x₂ = Asinωt = Acos(ωt - π/2)

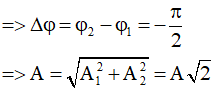
Câu 6. Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số có biên độ bằng nhau và bằng A nhưng pha ban đầu lệch nhau π/3 rad. Dao động tổng hợp có biên độ là

A. 1 A     B. √2A     C. 2A     D. √3A

Lời giải:

Biên độ dao động tổng hợp:

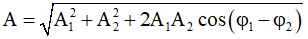
Theo bài ra thì hai dao động lệch pha nhau π/3 nên cos(φ₁ - φ₂) = cos(π/3) = 1/2

Vì thế biên độ dao động sẽ là:

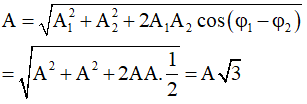
Câu 7. Một vật thực hiện đồng thời 2 dao động điều hoà cùng phương, cùng tần số có phương trình: x₁ = √3cos(ωt - π/2) cm, x₂ = cos(ωt) cm. Phương trình dao động tổng hợp:

A. x = 2√2cos(4πt - π/4) cm

B. x = 2√2cos(4πt + 3π/4) cm

C. x = 2cos(4πt - π/3) cm

D. x = 2cos(4πt + π/3) cm

Lời giải:

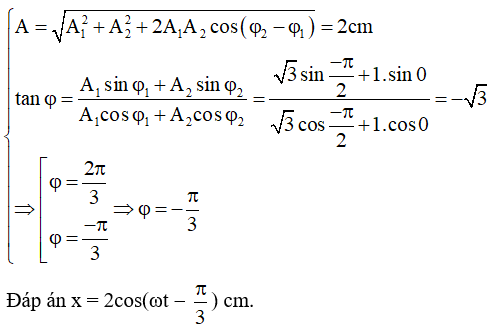
Câu 8. Một vật tham gia đồng thời ba dao động điều hòa cùng phương với các phương trình: x₁ = 5cos5πt (cm); x₂ = 3cos(5πt + π/2) (cm) và x₃ = 8cos(5πt - π/2) (cm). Xác định phương trình dao động tổng hợp của vật.

A. x = 5√2cos(5πt - π/4) cm

B. x = 5√2cos(5πt + 3π/4) cm

C. x = 5cos(5πt - π/3) cm

D. x = 5cos(5πt + 2π/3) cm

Lời giải:

Cách 1: Ta có: x₁ = 3sin(5πt + π/2) (cm) = 3cos5πt (cm)

x₂ và x₃ ngược pha nên: A₂₃ = 8 - 3 = 5 ⇒ x₂₃ = 5cos(5πt - π/2) (cm)

x₁ và x₂₃ vuông pha. Vậy: x = x₁ + x₂ + x₃ = 5√2cos(5πt - π/4) (cm)

Cách 2: Với máy FX570ES:

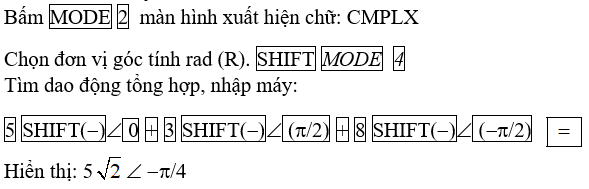
Câu 9. Dao động tổng hợp của hai dao động điều hòa cùng phương có biểu thức x = 5√3cos(6πt + π/2) (cm). Dao động thứ nhất có biểu thức là x₁ = 5cos(6πt + π/3)(cm). Tìm biểu thức của dao động thứ hai.

A. x₂ = 5√2cos(6πt - π/4) cm

B. x₂ = 5√2cos(6πt + 3π/4) cm

C. x₂ = 5cos(6πt - π/3) cm

D. x₂ = 5cos(6πt + 2π/3) cm

Lời giải:

Cách 1:

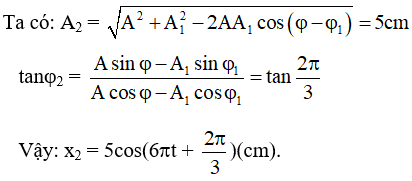
Cách 2: Với máy FX570ES :

Câu 10. Một chất điểm tham gia đồng thời 2 dao động điều hòa cùng phương trên trục Ox có phương trình x₁ = 2√3sinωt (cm) và x₂ = A₂cos(ωt + φ₂) (cm). Phương trình dao động tổng hợp x = 2cos(ωt + φ)(cm), với φ₂ - φ = π/3. Biên độ và pha ban đầu của dao động thành phần 2 là:

A. A₂ = 4 cm; φ₂ = π/6

B. A₂ = 4 cm; φ₂ = π/3

C. A₂ = 2√3 cm; φ₂ = π/4

D. A₂ = 4√3 cm; φ₂ = π/3

Lời giải:

Viết lại phương trình dao động của thành phần 1:

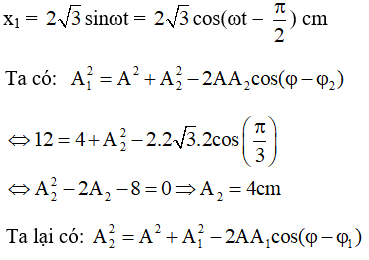
Câu 11. Cho hai dao động điều hoà cùng phương: x₁ = 2cos(4t + φ₁)cm và x₂ = 2cos(4t + φ₂)cm. Với 0 ≤ φ₂ - φ₁ ≤ π. Biết phương trình dao động tổng hợp x = 2 cos (4t + π/6) cm. Pha ban đầu φ₁ là:

A. π/2      B. -π/3     C. π/6       D. -π/6

Lời giải:

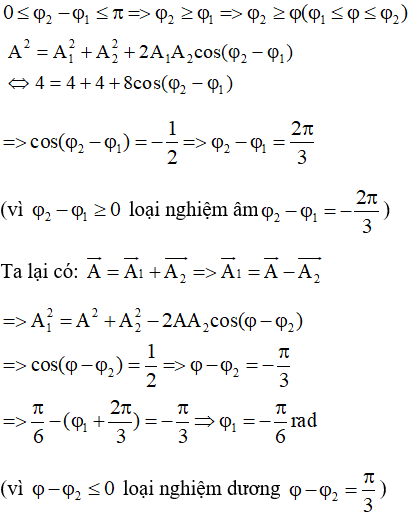
Câu 12. Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số có phương trình li độ x = 3cos(πt – 5π/6) (cm). Biết dao động thứ nhất có phương trình li độ x₁ = 5cos(πt + π/6) (cm). Dao động thứ hai có phương trình li độ là

A. x₂ = 8cos(πt + π/6) cm

B. x₂ = 2cos(πt + π/6) cm

C. x₂ = 2cos(πt – 5π/6) cm

D. x₂ = 8cos(πt – 5π/6) cm

Lời giải:

Nhận xét: ta thấy biên độ và pha đều cho rõ ràng nên cách giải nhanh nhất là dùng máy tính.

Câu 13. Một chất điểm tham gia đồng thời hai dao động có các phương trình: x₁ = A₁cos(ωt + π/2) (cm); x₂ = 5 cos(ωt + φ)(cm). Phương trình dao động tổng hợp là x = 5√3cos(ωt + π/3). Giá trị của A₁ bằng

A. 5,0 cm hoặc 2,5 cm.

B. 2,5√3 cm hoặc 2,5 cm

C. 5,0 cm hoặc 10 cm

D. 2,5√3 cm hoặc 10 cm

Lời giải:

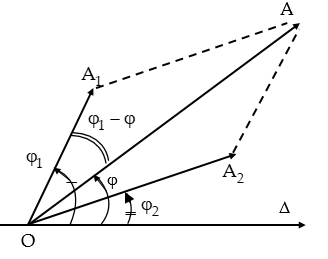
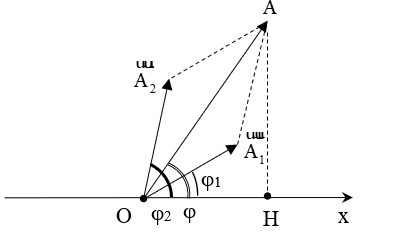
Áp dụng định lý hàm số cosin cho tam giác OA₁A

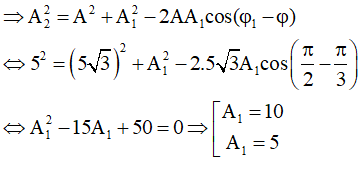
Câu 14. Một chất điểm tham gia đồng thời hai dao động có các phương trình: x₁ = A₁cos(ωt + π/2) (cm); x₂ = 5 cos(ωt + φ)(cm). Phương trình dao động tổng hợp là x = 5√3cos(ωt + π/3). Giá trị của A₁ bằng

A. 5,0 cm hoặc 2,5 cm.

B. 2,5√3 cm hoặc 2,5 cm

C. 5,0 cm hoặc 10 cm

D. 2,5√3 cm hoặc 10 cm

Lời giải:

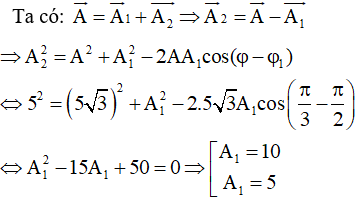
Câu 15. Cho hai dao động điều hoà cùng phương: x₁ = 2cos(4t + φ₁)cm và x₂ = 2cos(4t + φ₂)cm. Với 0 ≤ φ₂ - φ₁ ≤ π. Biết phương trình dao động tổng hợp x = 2cos(4t + π/6) cm. Pha ban đầu φ₁ là:

A. π/2     B. -π/3     C. π/6     D. -π/6

Lời giải:

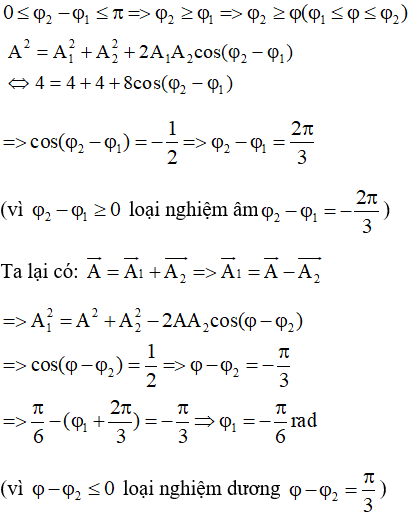
Chọn D