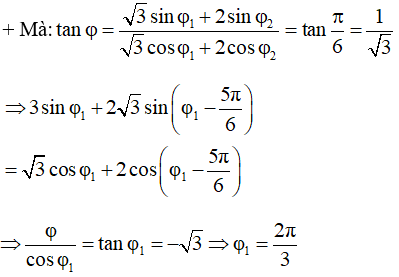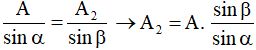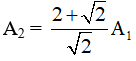Cách tìm điều kiện để biên độ A, A1, A2 đạt cực đại, cực tiểu hay, chi tiết - Vật Lí lớp 12

Cách tìm điều kiện để biên độ A, A1, A2 đạt cực đại, cực tiểu hay, chi tiết

Với Cách tìm điều kiện để biên độ A, A1, A2 đạt cực đại, cực tiểu hay, chi tiết Vật Lí lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm điều kiện để biên độ A, A1, A2 đạt cực đại, cực tiểu từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

A. Phương pháp & Ví dụ

1. Phương pháp

- Dựng các véc tơ A₁, A₂, A hoặc xây dựng được các biểu thức thể hiện mối quan hệ giữa đại lượng cần đánh giá cực trị với các đại lượng khác.

- Dựa vào yêu cầu của bài toán áp dụng định lí Sin trong tam giác

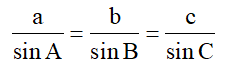
Hoặc sử dụng các bất đẳng thức như cosin, Bunhiacopxki, cực trị của hàm số để suy ra điều kiện cần tìm.

- Áp dụng các hệ thức lượng trong tam giác để tính toán kết quả.

2. Ví dụ

Ví dụ 1: Câu 18 – ĐH2012 – M371. Cho x₁ = A₁cos(πt + π/6) cm và x₂ = 6cos(πt – π/2) cm là phương trình của hai dao động cùng phương. Dao động tổng hợp của hai dao động này có phương trình x = Acos(πt + φ) cm. Thay đổi A₁ cho đến khi biên độ A đạt giá trị cực tiểu thì

A. φ = 0 rad.          B. φ = –π/3 rad.          C. φ = –π/6 rad.          D. φ = π rad.

Hướng dẫn:

Ví dụ 2: Một chất điểm tham gia đồng thời hai dao động cùng phương. Phương trình ly độ của các dao động thành phần và dao động tổng hợp lần lượt là x₁ = A₁cos(ωt) cm; x₂ = 3cos(ωt + α) cm; và x = Acos(ωt+ π/6) cm. Biên độ dao động A1 có giá trị lớn nhất là

A. 9 cm.          B. 6 cm.          C. 8 cm.          D. 12 cm.

Hướng dẫn:

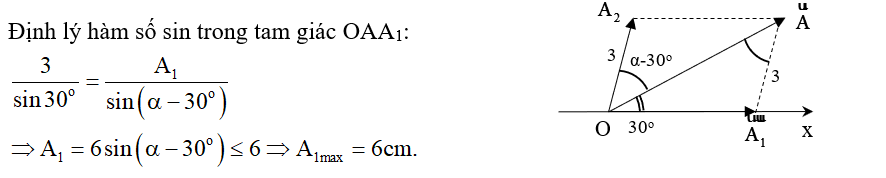
Ví dụ 3: Một chất điểm tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số, có phương trình là x₁ = A₁cos(ωt – π/3) và x₂ = A₂cos(ωt + π/3). Dao động tổng hợp có biên độ 4√3 cm. Khi A₁ đạt giá trị cực đại thì A₂ có giá trị là

A. 2 cm.          B. 3 cm.          C. 5 cm.          D. 4 cm.

Hướng dẫn:

Khi A₁ đạt giá trị cực đại

Độ lệch pha Δφ = π/3 – (-π/3) = 2π/3.

Áp dụng định lí hàm số sin trong tam giác OAA1:

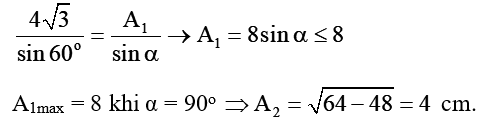
B. Bài tập trắc nghiệm

Câu 1. Hai dao động cùng phương lần lượt có phương trình x₁ = A₁cos(πt + π/6)(cm) và x₂ = 6cos(πt - π/2) (cm). Dao động tổng hợp của hai dao động này có phương trình x = Acos(πt + φ) (cm). Thay đổi A₁ cho đến khi biên độ A đạt giá trị cực tiểu thì

A. φ = -π/6 rad     B. φ = π rad

C. φ = -π/3 rad      D. φ = 0 rad

Lời giải:

Vẽ giản đồ như hình vẽ.

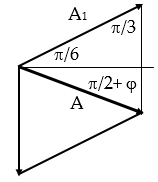
Theo định lí hàm sin:

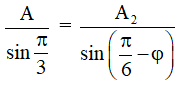
⇒ A đạt giá trị cực tiểu khi sin(π/6 - φ) = 1

Do đó φ = -π/3

Câu 2. Cho hai phương trình dao động điều hòa cùng phương cùng tần số có phương trình x₁ = A₁cos(4πt - π/6) cm và x₂ = A₂cos(4πt - π) cm. Phương trình dao động tổng hợp x = 9cos(4πt - φ) cm. Biết biên độ A₂ có giá trị cực đại. Giá trị của A₁ và phương trình dao động tổng hợp là:

A. x = 9√2cos(4πt - π/4) cm

B. x = 9√2cos(4πt + 3π/4) cm

C. x = 9cos(4πt - 2π/3) cm

D. x = 9cos(4πt + π/3) cm

Lời giải:

Vẽ giản đồ vectơ

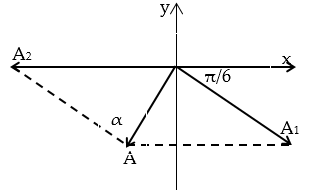
Dựa vào giản đồ vectơ. Áp đụng định lý hàm số sin

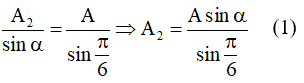
Từ (1) ⇒ khi α = 90°: A₂ = A/(1/2) = 2A = 18 cm

Tam giác OAA₂ vuông tại A, nên ta có:

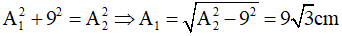
Xác định pha ban đầu tổng hợp

Dựa vào giản đồ vec tơ: φ = π/2 + π/6 = 2π/3

Vậy phương trình dao động tổng hợp là: C. x = 9cos(4πt - 2π/3) cm

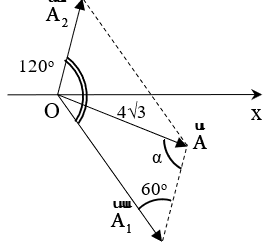
Câu 3. Hai dao động điều hoà cùng phương, cùng tần số có phương trình dao động x₁ = A₁cos(ωt + π/3) cm và x₂ = A₂cos(ωt - π/2) cm. Phương trình dao động tổng hợp của hai dao động này là: x = 6cos(ωt + φ) cm. Biên độ A₁ thay đổi được. Thay đổi A₁ để A₂có giá trị lớn nhất. Tìm A_2max?

A. 16 cm     B. 14 cm     C. 18 cm     D. 12 cm

Lời giải:

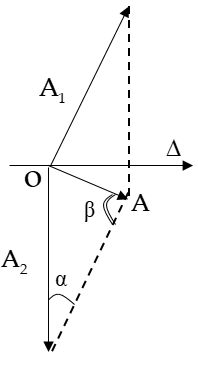
Độ lệch pha giữa 2 dao động: Δφ = 5π/6 rad không đổi.

Biên độ của dao động tổng hợp A = 6 cm cho trước.

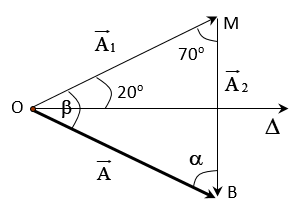
Biểu diễn bằng giản đồ vectơ như hình vẽ

Ta có:

Vì α, A không đổi nên A₂ sẽ lớn nhất khi sinβ lớn nhất tức là góc β = 90°.

Khi đó

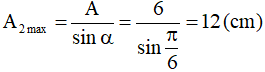
Câu 4. Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, theo các phương trình x₁ = 3cos(4t + π/2) cm và x₂ = A₂cos(4t) cm. Biết khi động năng của vật bằng một phần ba năng lượng dao động thì vật có tốc độ 8√3 cm/s. Biên độ A₂ bằng

A. 1,5 cm      B. 3 cm      C. 3√2 cm     D. 3√3 cm.

Lời giải:

Ta có

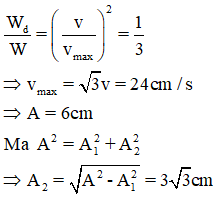
Câu 5. Một vật thực hiện đồng thời 3 dao động điều hòa cùng phương cùng tần số có phương trình là x₁, x₂, x₃. Biết x₁₂ = 6cos(πt + π/6) cm; x₂₃ = 6cos(πt + 2π/3) cm; x₁₃ = 6√2cos(πt + π/4) cm. Khi li độ của dao động x₁ đạt giá trị cực đại thì li độ của dao động x₃ là:

A. 0 cm       B. 3 cm     C. 3√2 cm     D. 3√6 cm

Lời giải:

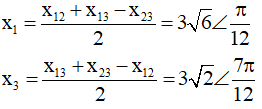
Ta thấy x₃ sớm pha hơn x₁ góc π/2 ⇒ x₁ max thì x₃ = 0.

Câu 6. Hai vật dao động điều hòa với phương trình x₁ = A₁cos20πt (cm), x₂ = A₂cos20πt (cm). Tính từ thời điểm ban đầu, thì cứ sau 0,125s thì khoảng cách 2 vật lại bằng A₁. Biên độ A₂ là

Lời giải:

+ Điều kiện để khoảng cách giữa hai vật là A₁ thì A₂ > A₁, lúc đó phương trình khoảng cách: Δx = x₂ – x₁ = (A₂ – A₁)cos20πt₁    (⋇)

+ Ở thời điểm t₁ + 0,125s có:

(A₂ – A₁)cos20π(t₁ + 0,125) = A₁ ⇔ (A₂ – A₁)cos(20πt₁ + 2,5π) = A₁      (⋇⋇)

+ Từ (⋇) và (⋇⋇): tan20πt₁ = 1 ⇒ tan20πt₁ = √2/2 thay vào (⋇) ta có được:

Câu 7. Hai chất điểm M và N dao động điều hòa cùng chu kì T = 4s dọc theo hai đường thẳng song song kề nhau và song song với trục Ox. Vị trí cân bằng của M và N đều ở trên cùng một đường thẳng qua gốc tọa độ và vuông góc với Ox. Trong quá trình dao động, khoảng cách lớn nhất giữa M và N theo phương Ox là 10 cm. Tại thời điểm t₁ hai vật đi ngang qua nhau, hỏi sau thời gian ngắn nhất là bao nhiêu kể từ thời điểm t₁ khoảng cách giữa chúng bằng 5√2 cm

A. 1 s     B. 1/3 s      C. 1/2 s      D. 1/6 s

Lời giải:

+ Chọn gốc thời gian là thời điểm hai vật đi ngang qua nhau thì phương trình khoảng cách giữa hai vật có thể chọn Δx = x₂ - x₁ = 10sin(0,5πt) cm

+ Thời gian ngắn nhất để hai vật cách nhau 5 cm là thời gian ngắn nhất đi từ Δx = 0 đến Δx = 5 cm là: T/8 = 1/2 s.

Câu 8. Cho hai phương trình dao động điều hòa cùng phương cùng tần số có phương trình x₁ = A₁cos(4πt - π/6) cm và x₂ = A₂cos(4πt - π) cm. Phương trình dao động tổng hợp x = 9cos(4πt - φ) cm. Biết biên độ A₂ có giá trị cực đại. Giá trị của A₁; A₂ và φ là:

A. A₁ = 9√3 cm; A₂ = 18 cm; φ = -2π/3 rad

B. A₁ = 9 cm; A₂ = 9√3 cm; φ = π/3 rad

C. A₁ = 9√3 cm; A₂ = 9 cm; φ = 2π/3 rad

D. A₁ = 9 cm; A₂ = 18 cm; φ = -π/3 rad

Lời giải:

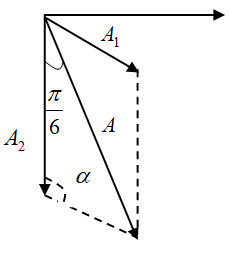
Độ lệch pha giữa thành phần tổng hợp với

Thành phần thứ hai: φ - φ₂ = -π/3 + π/2 = π/6

Theo định lý hàm sin:

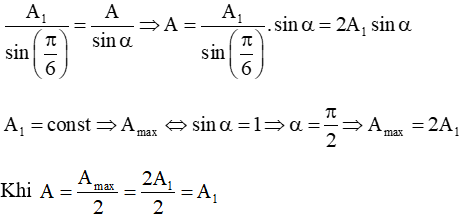
Ta lại có: A₁² = A² + A₂² - 2AA₂cos(φ - φ₂) ⇔ A₂² - 2A₁A₂cos(π/6) = 0

⇒ A₂ = √3A₁ = 10√3 cm. Chọn A.

Câu 9. (ĐH 2014) Cho hai dao động điều hòa cùng phương với các phương trình lần lượt là x₁ = A₁cos(ωt + 0,35) cm và x₂ = A₂cos(ωt - 1,57) cm . Dao động tổng hợp của hai dao động này có phương trình là x = 20cos(ωt + φ). Giá trị cực đại của (A₁ + A₂) gần giá trị nào nhất sau đây?

A. 25 cm     B. 20 cm     C. 40 cm     D. 35 cm

Lời giải:

Theo bài ra:

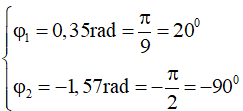
Áp dụng định lí hàm số sin:

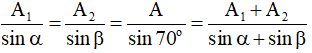
⇒ ΔOMB cân tại M

. Chọn D

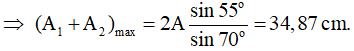
Câu 10. (Trích đề thi thử chuyên Hà Tĩnh lần 2 năm 2013): Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số có biên độ bằng trung bình cộng của hai biên độ thành phần và lệch pha so với dao động thành phần thứ nhất là 90°. Độ lệch pha của hai dao động thành phần đó là:

A. 120°     B. 126,9°     C. 105°     D. 143,1°

Lời giải:

Câu 10

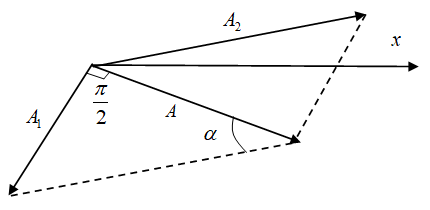
Áp dụng định lý hàm sin:

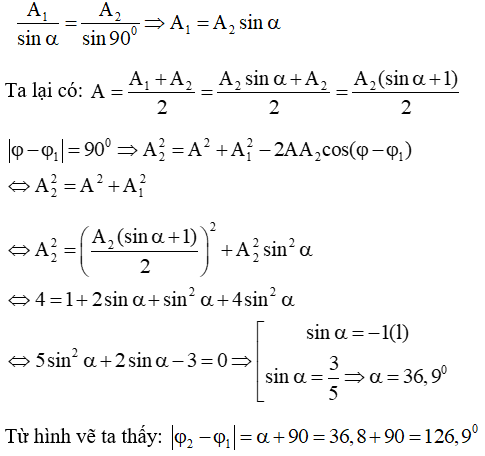
Chọn B

Một vật thực hiện đồng thời 3 dao động điều hòa cùng phương cùng tần số có phương trình là x₁, x₂, x₃. Biết x₁₂ = 6cos(πt + π/6) cm; x₂₃ = 6cos(πt + 2π/3) cm; x₁₃ = 6√2cos(πt + 5π/12) cm. Tính x biết x² = x₁² + x₃²

A. 6√2 cm     B. 12 cm      C. 24 cm     D. 6√3 cm

Lời giải:

Câu 11

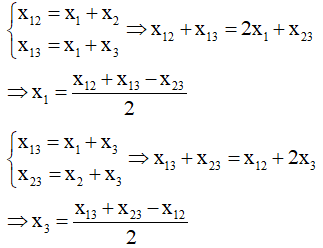
Sử dụng máy tính fx 570Es (plus) ta được:

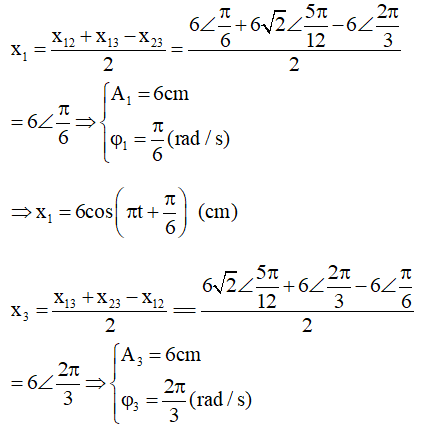
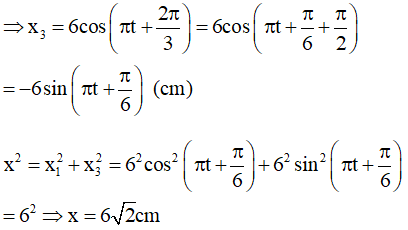
Chọn A

Câu 12. Cho ba vật dao động điều hòa cùng tần số, cùng khối lượng, dao động trên những trục song song kề nhau và song song với trục Ox với phương trình lần lượt x₁ = Acos(ωt + φ₁) cm, x₂ = Acos(ωt + φ₂) cm và x₃ = Acos(ωt + φ₃) cm. Biết tại mọi thời điểm thì động năng của chất điểm thứ nhất luôn bằng thế năng của chất điểm thứ hai và li độ của ba chất điểm thỏa mãn hệ thức -x₁² = x₂.x₃. Tại thời điểm mà khoảng cách giữa x₂ và x₃ bằng 2A/√3 thì tỉ số giữa động năng của chất điểm thứ nhất so với chất điểm thứ ba là

A. 9/11     B. 11/9     C. 9/4     D. 4/9

Lời giải:

+ Ta có E_đ1 = E_t2 ⇔ mω²(A² - x₁²) = mω²x₂² ⇔ x₁² + x₂² = A²

+ Tại mọi thời điểm : -x₁² = x₂.x₃ ⇒ x₂² - A² = x₂x₃ ⇔ x₂(x₂ - x₃) = A²

+ Khi khoảng cách giữa hai chất điểm 2 và 3 là 2A/√3 ta có :

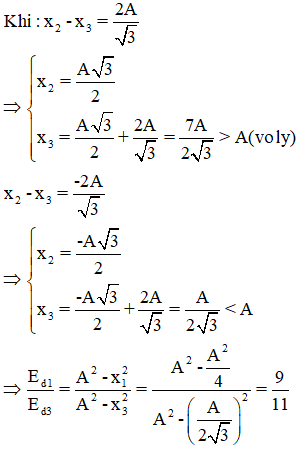
Chọn A

Câu 13. Một chất điểm tham gia đồng thời ba dao động điều hòa có phương trình x₁ = 2cos(ωt) cm; x₂ = 2cos(ωt + φ₂) cm và x₃ = 2cos(ωt + φ₃) cm với φ₃ ≠ φ₂ và 0 ≤ φ₃; φ₂ ≤ π. Dao động tổng hợp của x₁ và x₂ có biên độ là 2 cm, dao động tổng hợp của x₁ và x₃ có biên độ 2√3 cm. Độ lệch pha giữa hai dao động x₂ và x₃ là

A. 5π/6      B. π/3     C. π/2      D. 2π/3

Lời giải:

Nhận thấy biên độ các dao động thành phần bằng nhau nên:

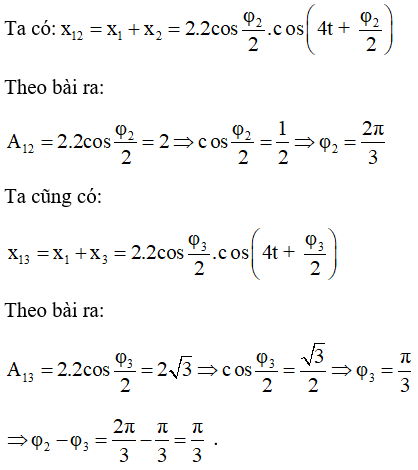
Chọn B

Câu 14. Hai vật dao động điều hòa cùng phương, cùng tần số có phương trình lần lượt là x₁ = A₁cos(ωt + φ₁) và x₂ = A₂cos(ωt + φ₂). Gọi x₍₊₎ = x₁ + x₂ và x_(-) = x₁ - x₂. Biết rằng biên độ dao động của x₍₊₎ gấp 3 lần biên độ dao động của x_(-). Độ lệch pha cực đại giữa x₁ và x₂ gần nhất với giá trị nào sau đây ?

A. 50°     B. 40°     C. 30°     D. 60°

Lời giải:

+ Ta có:

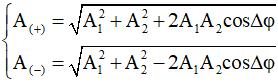
+ Mà: A₍₊₎ = 3A_(-) ⇒ 20A₁A₂cosΔφ = 8(A₁² + A₂²) ≥ 16A₁₂

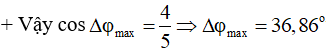
Vậy giá trị gần nhất với Δφ_max là 40°. Chọn B

Câu 15. (Chuyên Lương Văn Tụy – Ninh Bình lần 2/2016) Ba chất điểm M₁, M₂ và M₃ dao động điều hòa trên ba trục tọa độ song song cách đều nhau với các gốc tọa độ tương ứng O₁, O₂ và O₃ như hình vẽ. Khoảng cách giữa hai trục tọa độ liên tiếp là a = 2 cm. Biết rằng phương trình dao động của M₁ và M₂ là x₁ = 3cos2πt (cm) và x₂ = 1,5cos(2πt + π/3) (cm). Ngoài ra, trong quá trình dao động, ba chất điểm luôn luôn thẳng hàng với nhau. Khoảng cách lớn nhất giữa hai chất điểm M₁ và M₃ gần giá trị nào nhất sau đây?

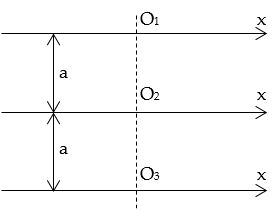
A. 6,56 cm

B. 5,20 cm

C. 5,57 cm

D. 5,00 cm

Lời giải:

+ Điều kiện để 3 chất điểm luôn thẳng hàng là: x₂ = (x₁ + x₃)/2

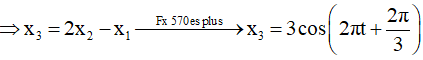
+ Khoảng cách cực đại giữa hai chất điểm M₁ và M₃ là:

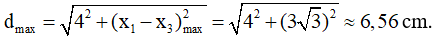
Chọn A

Câu 16. Một vật tham gia đồng thời hai dao động điều hoà cùng phương, cùng tần số và có dạng phương trình x₁ = √3cos(4t + φ₁) cm, x₂ = 2cos(4t + φ₂) cm với 0 ≤ φ₁ − φ₂ ≤ π. Biết phương trình dao động tổng hợp x = cos(4t + π/6) cm. Giá trị φ₁ là

A. 2π/3     B. –π/6       C. π/6     D. −2π/3

Lời giải:

Ta có 1 = 3 + 4 + 2(√3).2.cosΔφ

⇒ Δφ = 5π/6 = φ₁ - φ₂

⇒ φ₂ = φ₁ - 5π/6