Các dạng bài tập Giao thoa ánh sáng có lời giải - Vật Lí lớp 12
Các dạng bài tập Giao thoa ánh sáng có lời giải
Với Các dạng bài tập Giao thoa ánh sáng có lời giải Vật Lí lớp 12 tổng hợp các dạng bài tập, 100 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Giao thoa ánh sáng từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

- Dạng 2 : Bài tập Hiện tượng giao thoa ánh sáng trong đề thi Đại học có giải chi tiết Xem chi tiết
Cách giải bài tập Giao thoa với ánh sáng đơn sắc
A. Phương pháp & Ví dụ
Dạng 1.1. Vị trí vân sáng, vân tối - khoảng vân
a- Khoảng vân: là khoảng cách giữa 2 vân sáng liền kề
i = λD / a ( i phụ thuộc λ ⇒ khoảng vân của các ánh sáng đơn sắc khác nhau là khác nhau với cùng một thí nghiệm).
b- Vị trí vân sáng bậc k: Tại đó ứng với Δd = d2 – d1 = k.λ , đồng thời 2 sóng ánh sáng truyền tới cùng pha
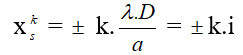
Để A là vân sáng trung tâm thì
k = 0 hay d = 0
k = 0: ứng với vân sáng trung tâm
k = 1: ứng với vân sáng bậc 1
…………
k = n: ứng với vân sáng bậc n.
c- Vị trí vân tối thứ k + 1: Tại đó ứng với Δd = (k + 0,5 ).λ . Là vị trí hai sóng ánh sáng truyền tới ngược pha nhau.
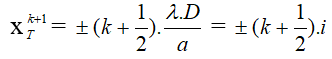
Hay vân tối thứ k:
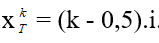
Ví dụ
Vị trí vân sáng bậc 5 là:
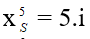
Vị trí vân tối thứ 4:
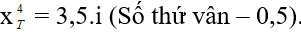
Dạng 1.2. Khoảng cách giữa các vân
Loại 1- Khoảng cách vân cùng bản chất liên tiếp: l = (số vân – 1).i
Ví dụ: khoảng cách giữa 7 vân sáng liên tiếp: l = (7 – 1).i = 6i
Loại 2- Giữa một vân sáng và một vân tối bất kỳ:
Giả sử xét khoảng cách vân sáng bậc k và vân tối thứ k’, vị trí:
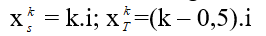
Nếu:
+ Hai vân cùng phía so với vân trung tâm:
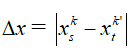
+ Hai vân khác phía so với vân trung tâm:
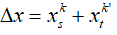
-Khoảng cách giữa vân sáng và vân tối liền kề là : i/2 nên vị trí vân tối các thứ liên tiếp được xác định: xt = ki / 2 (với k lẻ: 1,3,5,7,….)
VD: Tìm khoảng cách giữa vân sáng bậc 5 và vân tối thứ 6
Giải:
Ta có
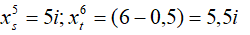
+ Nếu hai vân cùng phía so với vân trung tâm:
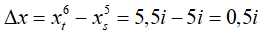
+ Nếu hai vân khac phía so với vân trung tâm :
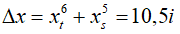
Loại 3- Xác định vị trí một điểm M bất kì trên trường giao thoa cách vân trung tâm một khoảng xM có vân sáng hay vân tối, bậc mấy ?
+ Lập tỉ số:
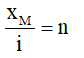
Nếu n nguyên, hay n ∈ Z, thì tại M có vân sáng bậc k=n.
Nếu n bán nguyên hay n = k + 0,5 với k Z, thì tại M có vân tối thứ k +1
Ví dụ
Ví dụ: Một khe hẹp F phát ánh sáng đơn sắc bước sóng λ = 600nm chiếu sáng hai khe song song với F và cách nhau 1m. Vân giao thoa được quan sát trên một màn M song song với màn phẳng chứa F1 và F2 và cách nó 3m. Tại vị trí cách vân trung tâm 6,3m có
A. Vân tối thứ 4 B. Vân sáng bậc 4 C. Vân tối thứ 3 D. Vân sáng bậc 3
Hướng dẫn:
Ta cần xét tỉ số x / i
Khoảng vân i= λD / a = 1,8mm, ta thấy 6,3 / 1,8 = 3,5 là một số bán nguyên nên tại vị trí cách vân trung tâm 6,3mm là một vân tối
Mặt khác xt = (k + 0,5)i= 6,3 nên ( k+ 0,5 )=3,5 nên k= 3. Vậy tại vị trí cách vân trung tâm 6,3mm là một vân tối thứ 4 vậy chọn đáp án A
Dạng 1.3. Xác định số vân trên trường giao thoa
- Trường giao thoa xét là chiều rộng của khu vực chứa toàn bộ hiện tượng giao thoa hứng được trên màn- kí kiệu L.
- Số vân trên trường giao thoa:
+ Số vân sáng:
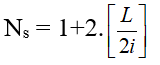
+ Số vân tối:
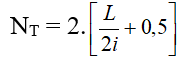
- Số vân sáng, vân tối trong đoạn MN, với 2 điểm M, N thuộc trường giao thoa nằm 2 bên vân sáng trung tâm:
+ Số vân sáng:
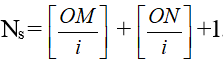
+ Số vân tối:
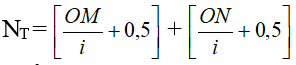
- Số vân sáng, tối giữa 2 điểm MN trong đoạn giao thoa nằm cùng phía so với vân sáng trung tâm:
+ Số vân sáng:
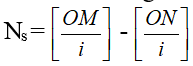
+ Số vân tối:
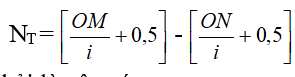
Với M, N không phải là vân sáng.
Ví dụ
Ví dụ: Trong một thí nghiệm về Giao thoa anhs sáng bằng khe I âng với ánh sáng đơn sắc λ = 0,7 μ m, khoảng cách giữa 2 khe s1,s2 là a = 0,35 mm, khoảng cách từ 2 khe đến màn quan sát là D = 1m, bề rộng của vùng có giao thoa là 13,5 mm. Số vân sáng, vân tối quan sát được trên màn là:
A: 7 vân sáng, 6 vân tối; B: 6 vân sáng, 7 vân tối.
C: 6 vân sáng, 6 vân tối; D: 7 vân sáng, 7 vân tối.
Hướng dẫn:
Ta có khoảng vân
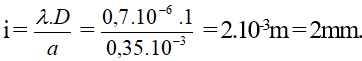
Số vân sáng:
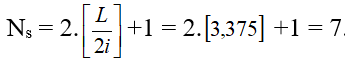
Do phân thập phân của L/2i là 0,375 < 0,5 nên số vạch tối là NT = Ns – 1 = 6 Số vạch tối là 6, số vạch sáng là 7. đáp án A.
Bài tập vận dụng
Trong thí nghiệm ánh sáng giao thoa với khe I âng, khoảng cách giữa 2 khe s1, s2 là 1mm, khoảng cách từ 2 khe đến màn quan sát là 2 mét. Chiếu vào 2 khe ánh sáng có bước sóng λ = 0,656 m. Biết bề rộng của trường giao thoa lag L = 2,9 cm. Xác định số vân sáng, tôi quan sát được trên màn.
A: 22 vân sáng, 23 vân tối; B: 22 vân sáng, 21 vân tối
C: 23 vân sáng, 22 vân tối D: 23 vân sáng, 24 vân tối
Dạng 1.4. Giao thoa với khe Young (Iâng) trong môi trường có chiết suất là n và thay đổi khoảng cách.
Gọi λ là bước sóng ánh sáng trong chân không hoặc không khí.
Gọi λ' là bước sóng ánh sáng trong môi trường có chiết suất n.
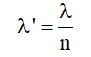
a. Vị trí vân sáng:
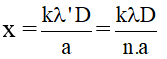
b.Vị trí vân tối:
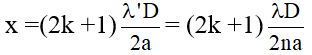
c. Khoảng vân:
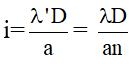
d. Khi thay đổi khoảng cách:
+ Ta có: i = λD / a ⇒ i tỉ lệ với D ⇒ khi khoảng cách là D: i = λD / a
khi khoảng cách là D’:
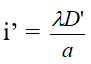
Nếu D = D’ – D > 0. Ta dịch màn ra xa (ứng i’ > i)
Nếu D = D’ – D < 0. Ta đưa màn lại gần ( ứng i’ < i).
Ví dụ
Ví dụ: Một khe hẹp F phát ánh sáng đơn sắc λ = 600nm, chiếu vào khe I âng có a = 1,2mm, lúc đầu vân giao thoa được quan sát trên một màn M đặt cách một mặt phẳng chứa S1, S2 là 75cm. Về sau muốn quan sát được vân giao thoa có khoảng vân 0,5mm thì cần phải dịch chuyển màn quan sát so với vị trí đầu như thế nào?
Hướng dẫn:
Ta có
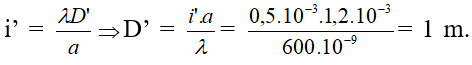
Vì lúc đầu D = 75cm = 0,75m nên phải dịch chuyển màn quan sát ra xa thêm một đoạn D’- D = 0,25m.
Bài tập vận dụng
Bài tập Thí nghiệm giao thoa ánh sáng đơn sắc bằng khe I âng. Khi khoảng cách từ 2 khe đến màn là D thì điểm M trên màn là vân sáng bậc 8. Nếu tịnh tiến màn xa 2 khe một đoạn 80 cm dọc đường trung trực của 2 khe thì điểm M là vân tối thứ 6. Tính D?
Dạng 1.5. Đặt bản mỏng trước khe Young
Trong thí nghiệm giao thoa ánh sáng với khe Young (I-âng), nếu ta đặt trước khe S1 một bản thủy tinh có chiều dày e, chiết suất n.
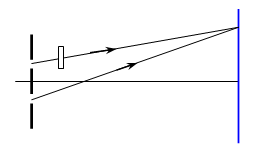
Khi đặt bản mỏng trước khe S1 thì đường đi của tia sáng S1M và S2M lần lượt là:
S1M = d1 + (n - 1)e
S2M = d2
Hiệu quang trình:
δ = S2M - S1M = d2 – d1 – (n – 1)e
Mà d2 – d1 = ax/D.
δ = ax/D – (n – 1)e
Vân sáng trung tâm ứng với hiệu quang trình bằng δ = 0.
δ = axo/D – (n – 1)e = 0
Hay: xo = (n - 1)eD / a.
Hệ thống vân dịch chuyển về phía S1. Vì xo>0.
Ví dụ
Ví dụ: Thí nghiệm giao thoa ánh sáng đơn sắc bằng khe I âng biết a = 0,5mm, D = 2m.. Khoảng cách giữa 6 vân sáng liên tiếp dài 1,2cm, về sau nếu sau khe S1 chắn 1 tấm thủy tinh phẳng mỏng có n = 1,5 thì vân sáng chính giữa bị dịch chuyển đến vị trí vân sáng bậc 20 ban đầu. tìm bề dày e của tấm thủy tinh này?
Hướng dẫn:
Ta có độ dịch chuyển của hệ vân giao thoa = độ dịch chuyển của vân trung tâm.
Lúc đầu:
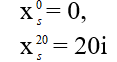
lúc sau:
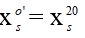
⇒ Độ dịch chuyển của hệ là
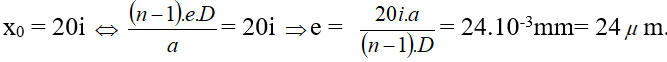
Chú ý:
+ Nếu đặt hai bản mỏng như nhau trên cả hai đường truyền S1, S2 thì hệ vân không dịch chuyển.
+ Nếu đặt hai bản mỏng khác nhau trên cả hai đường chuyền thì độc dịch chuyển của hệ vân là |xe1 - xe2|
Bài tập vận dụng
Bài tập Trong thí nghiệm I âng về giao thoa ánh sáng, khoảng cách 2 khe hẹp = 0,2mm, D = 1m. Nếu đặt trước một trong hai nguồn sáng một bản mỏng bề dày e = 0,01mm, n = 1,5 có hai mặt song song nhau thì độ dịch chuyển của hệ thống vân trên màn là bao nhiêu?
Hướng dẫn:
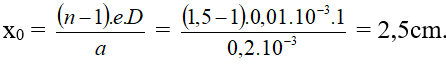
Dạng 1.6. Tịnh tiến khe sáng S đoạn y0
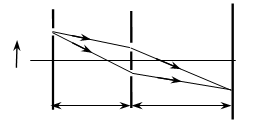
Trong thí nghiệm Young về giao thoa ánh sáng, nguồn sáng S phát ánh sáng đơn sắc có bước sóng λ. Khoảng cách từ nguồn S đến mặt phẳng chứa hai khe S1; S2 là d. Khoảng cách giữa hai khe S1; S2 là a , khoảng cách từ mặt phẳng chứa hai khe tới màn quan sát là D.
Tịnh tiến nguồn sáng S theo phương S1 S2 về phía S1 một đoạn y thì hệ thống vân giao thoa di chuyển theo chiều ngược lại đoạn xo: xo = yD / d
Ví dụ
Ví dụ: Trong thí nghiệm giao thoa ánh sáng bằng khe I âng, có D = 1m, khoảng cách từ nguồn S đến 2 khe là d = 20cm. Nếu dịch chuyển nguồn sáng S một đoạn theo phương vuông góc với trụ đối xứng của hệ thì hệ vân trên màn sẽ dịch chuyển như thế nào?
Hướng dẫn:
Từ hình vẽ trên ta có: điểm O’ với hiệu quang trình là:
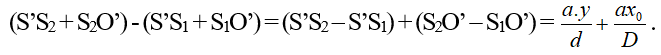
Muốn O’ là vạch sáng thì
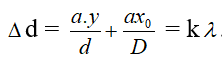
Và O’ là vạch sáng trung tâm khi k = 0, lúc đó
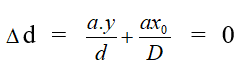
x = -Dy / d . Dấu (-) chứng tỏ vân trung tâm sẽ dịch chuyển ngược chiều so với nguồn sáng S một khoảng
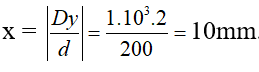
Bài tập vận dụng
Bài tập Trong thí nghiệm I âng về giao thoa ánh sáng, khoảng cách giữa 2 khe sáng a = 0,5 mm, khoảng cách từ khe S đến mặt phẳng chứa 2 khe là d = 50cm. Khe S phát ra ánh sáng đơn sắc có λ =0,5 m. Chiếu sáng 2 khe hẹp. Để một vân tối chiếm chỗ của một vân sáng liền kề, ta phải dịch chuyển khe S theo phương S1,S2 một đoạn b = bao nhiêu?
Hướng dẫn:
Ta có độ dịch chuyển vân trung tâm là x = bD / d
Để cho vân tối đến chiếm chiếm chỗ của vân sáng liền kề thì hệ vân phải dịch chuyển một đoạn i/2 , tức là:
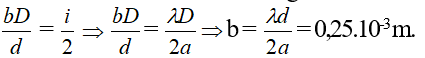
Cách giải bài tập Giao thoa với ánh sáng đa sắc
A. Phương pháp & Ví dụ
Nhận xét
Khi cho chùm đa sắc gồm nhiều bức xạ chiếu vào khe Y-âng để tạo ra giao thoa. Trên màn quan sát được hệ vân giao thoa của các bức xạ trên. Vân trung tâm là sự chồng chập của các vân sáng bậc k = 0 của các bức xạ này. Trên màn thu được sự chồng chập: của các vạch sáng trùng nhau, các vạch tối trùng nhau hoặc vạch sáng trùng vạch tối giữa các bức xạ này.
Ta có: Giao thoa của hai hay nhiều bức xạ:
Dạng 2.1. Vị trí vân sáng trùng:
k1i1 = k2i2⇒...⇒k1 λ1 ⇒ k2 λ2
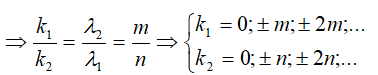
Hoặc ta có thể xác định:Vị trí vân sáng của các bức xạ đơn sắc trùng nhau
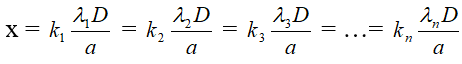
k1λ1 = k2λ2 = k3λ3 = k4λ4 = .... = knλn với k1, k2, k3,…, kn ∈ Z
Dựa vào phương trình biện luận chọn các giá trị k thích hợp, thông thường chọn k là bội số của số nguyên nào đó.
Ví dụ:
Hai bức xạ λ1 và λ2 cho vân sáng trùng nhau. Ta có k1λ1 = k2λ2 ⇒
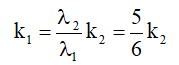
Vì k1, k2 là các số nguyên, nên ta chọn được k2 là bội của 6 và k1 là bội của 5
Có thể lập bảng như sau:
| k1 | 0 | 5 | 10 | 15 | 20 | 25 | ..... |
| k2 | 0 | 6 | 12 | 18 | 24 | 30 | ..... |
| x | 0 | ..... | ..... | ..... | ..... | ..... | ..... |
Dạng 2.2. Khoảng vân trùng
(khoảng cách nhỏ nhất giữa hai vân cùng màu với vân trung tâm):
i12 = mi1 = ni2 = ...
hoặc: i12 = BCNN(i1, i2)
Ba bức xạ: i12 = BCNN(i1, i2, i3)
Dạng 2.3. Xét cụ thể với chùm sáng gồm 2 bức xạ λ1, λ2
Loại 1: Vị trí hai vân sáng trùng nhau. Ngoài cách tổng quát trên ta có thể làm như sau:
+ Số vạch trùng quan sát được. Số vạch sáng quan sát được:
Khi có giao thoa: Vị trí vân sáng:
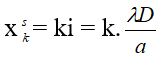
Khi 2 vân sáng của 2 bức xạ trùng nhau:
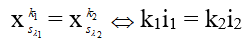
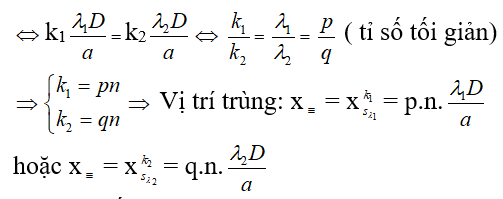
+ Số vạch trùng quan sát được trên trường giao thoa L:
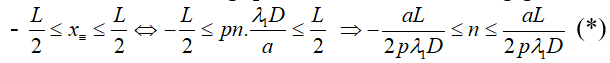
mỗi giá trị n → 1 giá trị k ⇒ số vạch sáng trùng là số giá trị n thỏa mãn (*).
+ Xét số vân trùng trên MN− ∈ L:
xM ≤ x ≡ ≤ xN (xM < xN; x là tọa độ) ⇒ khoảng n ⇒số giá trị n là số vân sáng trùng thuộc + Xét số vân trùng trên MN−.
Chú ý: Nếu M,N là vân sáng trùng ⇒ dùng dấu “ = „.
+ Số vạch quan sát được trên trường L:
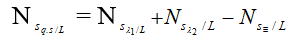
+ Số vạch quan sát được trên MN− L:
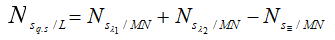
( Nhớ chú ý M,N có phải là vân sáng trùng không )
Ví dụ
Ví dụ : Trong thí nghiệm về giao thoa ánh sáng qua khe I-Âng có a= 2mm D=2m, nguồn sáng gồm hai bức xạ λ1 = 0,5μm, λ2 = 0,4μm. Tìm số vân sáng quan sát được trên trường giao thoa ?
Hướng dẫn:
Ta có :
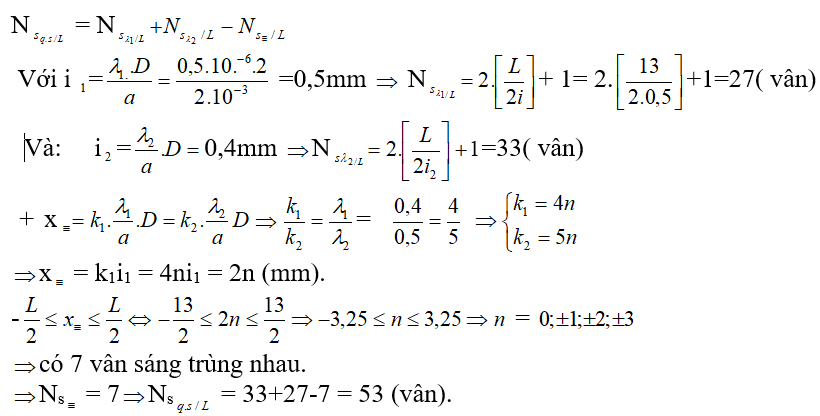
+ Bậc trùng nhau của từng bức xạ và vị trí trung nhau:
BT trên; Tìm khoảng cách giữa 2 vân sáng trùng nhau gần nhau nhất?
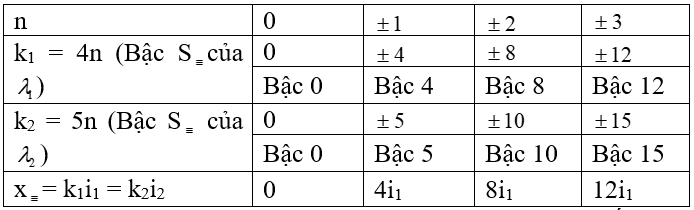
Nhận xét: Khoảng cách giữa 2 vân sáng trùng nhau liên tiếp là như nhau và là 4i1 hay 5i2.
Trong bài này là
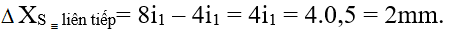
Loại 2: Hai vân tối trùng nhau của hai bức xạ:
- Khi vân tối của 2 bức xạ trùng nhau:
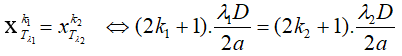

Vị trí trùng: x
xT≡ nằm trong vùng khảo sát:
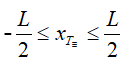
+ Số vân xT≡ trong trường giao thoa:
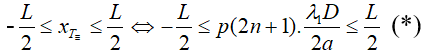
Số giá trị của n thỏa mãn (∗)⇒ số vân tối trùng trong trường giao thoa.
+ Số vân xT≡ trong miền MN−L:
xM ≤xT≡ ≤xN (xM; xN là tọa độ và xM < xN (∗∗)
Số vân tối trùng trong vùng MN− là số giá trị n thỏa mãn (∗∗)
Ví dụ
Ví dụ: Trong thí nghiệm giao thoa I âng thực hiện đồng thời hai bức xạ đơn sắc với khoảng vân trên màn thu được lần lượt là: i1 = 0,5mm; i2 = 0,3mm. Biết bề rộng trường giao thoa là 5mm, số vị trí trên trường giao thoa có 2 vân tối của hai hệ trùng nhau là bao nhiêu?
Hướng dẫn:
Khi 2 vân tối trùng nhau:
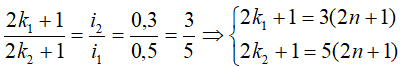
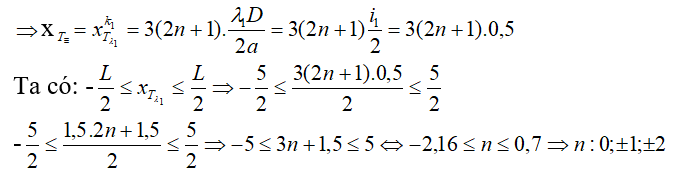
⇒có 4 vị trí vân tối trùng nhau trên trường giao thoa L.
Loại 3: Vân sáng của bức xạ này trùng vân tối của bức xạ kia.
- Giả sử:
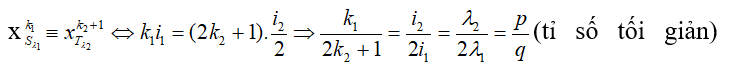
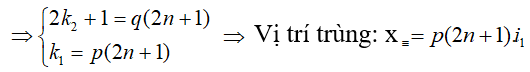
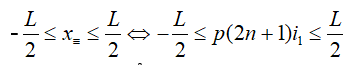
⇒số vân sáng trùng vân tối là số giá trị của n thỏa mãn biểu thức này
Chú ý: Có thể xét xTλ1 = xTλ2
Ví dụ
Ví dụ: Trong thí nghiệm giao thoa I âng, thực hiện đồng thời với 2 ánh sáng đơn sắc khoảng vân giao thoa trên màn lần lượt i1 = 0,8mm, i2 = 0,6mm. Biết trường giao thoa rộng: L = 9,6mm. Hỏi số vị trí mà :
a) xTλ1 = xSλ2 . ( -2,5 ≤ n ≤ 1,5 : có 4 vị trí)
b) xSλ1 = xTλ2
Hướng dẫn:
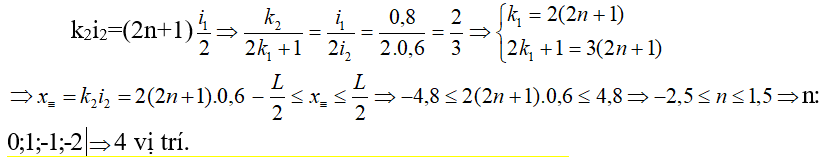
Cách giải bài tập Giao thoa với ánh sáng trắng
A. Phương pháp & Ví dụ

∗ Nhận xét: Khi thực hiện giao thoa với ánh sáng trắng ta thấy:
+ Ở chính giữa mỗi ánh sáng đơn sắc đều cho một vạch màu riêng, tổng hợp của chúng cho ta vạch sáng trắng (Do sự chồng chập của các vạch màu đỏ đến tím tại vị trí này)
+ Do tím nhỏ hơn λtím⇒ λtím = itím.D/a nhỏ hơn và làm cho tia tím gần vạch trung tâm hơn so với tia đỏ (Xét cùng một bậc giao thoa)
+ Tập hợp các vạch từ tím đến đỏ của cùng một bậc (cùng giá trị k) ⇒ quang phổ của bậc k đó, (Ví dụ: Quang phổ bậc 2 là bao gồm các vạch màu từ tím đến đỏ ứng với k = 2).
Dạng 3.1. Cho tọa độ xo trên màn, hỏi tại đó có những bức xạ nào cho vạch tối hoặc sáng?
a. Các bức xạ của ánh sáng trắng cho vân sáng tại xo khi:
Tại xo có thể là giá trị đại số xác định hoặc là một vị trí chưa xác định cụ thể.
Vị trí vân sáng bất kì x = k λD / a
Vì x = xo nên
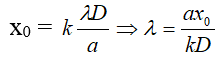
với điều kiện λ1 ≤ λ ≤ λ2,
thông thường λ1 =0,4.10-6m (tím) ≤ λ ≤ 0,75.10-6m = λ2 (đỏ)
Giải hệ bất phương trình trên,
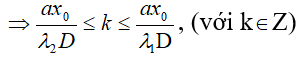
chọn k ∈ Z và thay các giá trị k tìm được vào tính λ với λ = axo / kD: đó là bước sóng các bức xạ của ánh sáng trắng cho vân sáng tại xo.
b. Các bức xạ của ánh sáng trắng cho vân tối (bị tắt) tại xo:
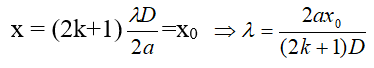
Với điều kiện:
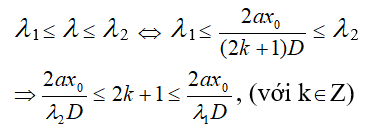
Thay các giá trị k tìm được vào :
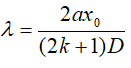
đó là bước sóng các bức xạ của ánh sáng trắng cho vân tối (bị tắt) tại xo.
Ví dụ
Ví dụ: Trong thí nghiệm I âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng trắng có bước sóng từ 380nm đến 760nm. Khoảng chách giữa 2 khe là 0,8mm, khoảng cách từ mặt phẳng chứa 2 khe đến màn là 2 m. Trên màn tại vị trí cách vân trung tâm 3mm có vân sáng của những bức xạ nào?
Hướng dẫn:
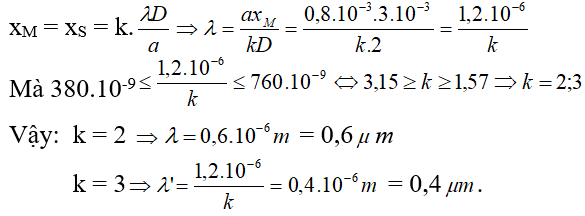
Dạng 3.2. Xác định bề rộng quang phổ bậc k trong giao thoa với ánh sáng trắng
Bề rộng quang phổ là khoảng cách giữa vân sáng màu đỏ ngoài cùng và vân sáng màu tím của một vùng quang phổ.
Δxk = xđk - xtk
Δxk = kD(λd - λd) / a
Δxk = k(iđ - it)
với k ∈ N, k là bậc quang phổ.
Ví dụ
Ví dụ: Trong thí nghiệm về giao thoa ánh sáng trắng có a = 3mm, D = 3m, bước sóng từ 0,4 đến 0,75 . Trên màn quan sát thu được các dải quang phổ. Bề rộng của dải quang phổ thứ 2 kể từ vân sáng trắng trung tâm là bao nhiêu?
Hướng dẫn:
Ta có: Bề rộng quang phổ bậc 2: