Chinh phục bài tập Đồ thị dao động điều hòa, dao động cơ có giải chi tiết - Vật Lí lớp 12

Chinh phục bài tập Đồ thị dao động điều hòa, dao động cơ có giải chi tiết

Với Chinh phục bài tập Đồ thị dao động điều hòa, dao động cơ có giải chi tiết Vật Lí lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Đồ thị dao động điều hòa, dao động cơ từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

A. Phương pháp & Ví dụ

I. KIẾN THỨC CƠ BẢN

1. Đồ thị dao động cơ

Xét phương trình dao động x = Acos(ωt + φ), chọn gốc thời gian và chiều dương trục tọa độ thích hợp sao cho φ = 0. Lập bảng biến thiên của li độ x theo thời gian và đồ thị biểu diễn x theo t như sau:

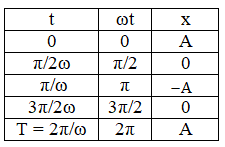
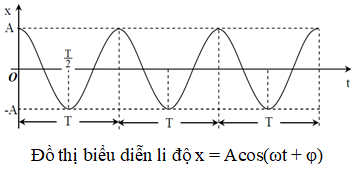
2. Đồ thị và sự so sánh pha của các dao động điều hòa: x, v, a.

Vẽ đồ thị của dao động x = Acos(ωt + φ) trong trường hợp φ = 0.

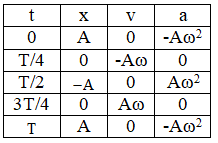
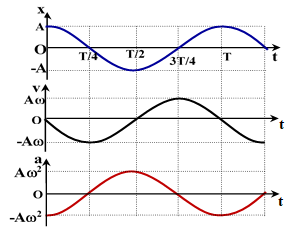
Nhận xét:

     + Nếu dịch chuyển đồ thị v về phía chiều dương của trục Ot một đoạn thì đồ thị của v và x cùng pha nhau. Nghĩa là, v nhanh pha hơn x một góc π/2 hay về thời gian là T/4.

     + Nếu dịch chuyển đồ thị a về phía chiều dương của trục Ot một đoạn thì đồ thị của a và v cùng pha nhau.

Nghĩa là, a nhanh pha hơn v một góc π/2 hay về thời gian là T/4.

     + Nhận thấy a và x luôn ngược pha nhau (trái dấu nhau).

3. Đồ thị x, v và a dao động điều hòa vẽ chung trên một hệ trục tọa độ

Vẽ đồ thị trong trường hợp φ = 0.

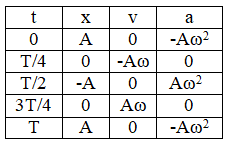
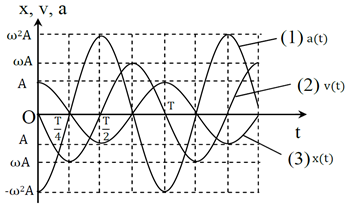
4. Đồ thị năng lượng trong dao động điều hòa

a. Sự bảo toàn cơ năng:

Dao động của con lắc đơn và con lắc lò xo dưới lực thế (trọng lực và lực đàn hồi, …) và không có ma sát nên cơ năng của nó được bảo toàn. Vậy cơ năng của vật dao động được bảo toàn.

b. Biểu thức thế năng:

Xét con lắc lò xo.

Tại thời điểm bất kỳ vật có li độ x = Acos(ωt + φ) và thế năng của con lắc lò xo có dạng:

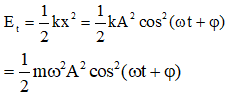
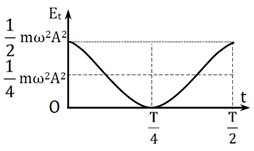
Ta có đồ thị E_t trong trường hợp φ = 0.

c. Biểu thức động năng

Ở thời điểm t bất kì vật có vận tốc v = -ωAsin(ωt + φ) và có động năng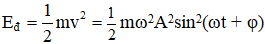

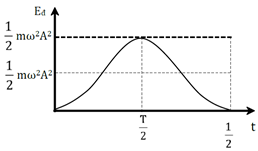
Ta có đồ thị E_đ trong trường hợp φ = 0.

d. Biểu thức cơ năng

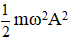
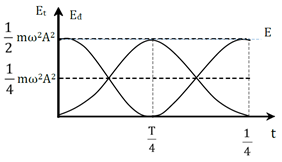
Cơ năng tại thời điểm t: E = E_đ + E_t = = hằng số

Ta có đồ thị E_đ và E_t vẽ trên cùng một hệ trục.

II. Phương pháp xác định phương trình từ đồ thị

a. Xác định biên độ

Nếu tại VTCB, x = 0, thì:

     + x = x_max = A (Từ số liệu trên đồ thị ta xác định được A).

     + v = v_max = ωA (Từ số liệu trên đồ thị ta xác định được v_max).

     + a = a_max = ω²A (Từ số liệu trên đồ thị ta xác định được a_max).

b. Xác định pha ban đầu φ

Nếu là hàm cos thì dùng các công thức:

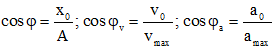
Sau đó dựa vào chiều tăng giảm của đồ thị tại thời điểm t = 0 ta xác định được dấu của pha ban đầu φ, φ_v, φ_a.

c. Xác định chu kì T (Suy ra tần số f hoặc tần số góc ω):

Nhận dạng thời điểm trạng thái lặp lại, hay chu kì T là khoảng thời gian giữa hai điểm cùng pha gần nhất. Rồi suy ra tần số f (hoặc tần số góc ω).

Dựa vào thời gian ghi trên đồ thị và pha ban đầu, vẽ lại đường tròn Fresnel để xác định góc quét tương ứng với thời gian sau đó áp dụng công thức tìm ω: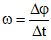

Lưu ý:

- Các đồ thị dao động điều hòa của li độ (x), vận tốc (v) và gia tốc (a) biến thiên điều hòa theo hàm số sin và cos với chu kì T.

- Các đồ thị đồng năng và thế năng biến thiên tuần hoàn theo hàm số sin và cos với chu kì T/2.

⋇ Vận dụng giải các bài tập về đồ thị, chúng ta quan sát đồ thị tìm ra các đại lượng dựa quy luật sau:

     + Tìm biên độ dao động dựa vào trục giới hạn cắt điểm nào đó trên trục tung (tìm biên độ A, ωA hoặc ω²A).

     + Tìm chu kì dao động dựa vào sự lặp lại trên trục thời gian, hoặc dựa vào khoảng thời gian gần nhất cùng pha để vật nhận giá trị nào đó.

     + Tại thời điểm t thì x = ?, v = ?, a = ? nhằm tìm được pha ban đầu φ và chu kì T. Suy ra tần số góc ω.

     + Dựa vào đường tròn và vận dụng các công thức của dao động tìm các đại lượng và các yếu tố cần tìm.

     Xác định chu kì T, rồi suy ra tần số f (hoặc tần số góc ω): Thường căn cứ vào số liệu trên trục thời gian.

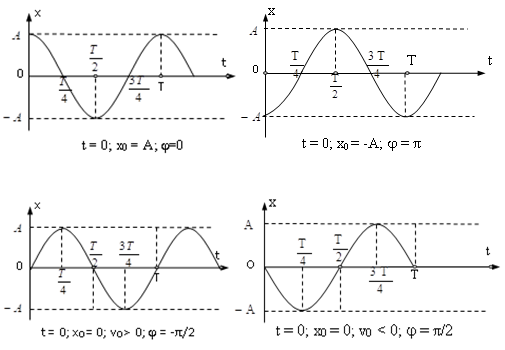
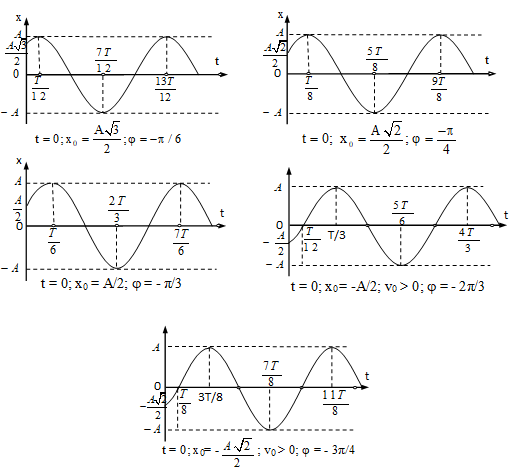
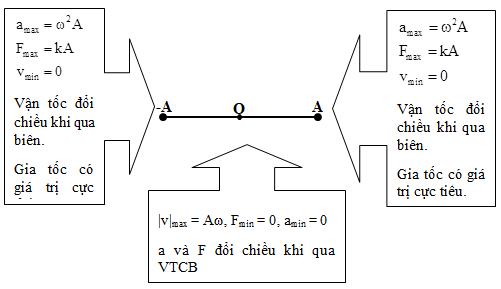
(Mô hình mối liên hệ giá trị của các đại lượng x, v, a, F tại các điểm đặc biệt: x = 0; x = - A; x = A)

2. Ví dụ

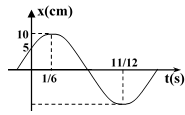
Ví dụ 1: Cho đồ thị của một dao động điều hòa.

a) Tính biên độ, tần số góc, chu kỳ, tần số.

b) Tính pha ban đầu của dao động.

c) Viết phương trình dao động.

d) Phương trình vận tốc.

e) Phương trình gia tốc.

f) Sau những khoảng thời gian liên tiếp bằng nhau và bằng bao nhiêu thì động năng lại bằng thế năng.

Hướng dẫn:

a) Dựa vào đồ thị ta có: A = 10cm. Tại thời điểm t = 0; x = 5cm; x đang tăng:

x = Acosφ →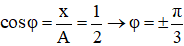

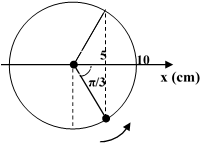
Vận dụng mối quan hệ giữa dao động điều hòa và chuyển động tròn đều:

Ta nhận xét vì x đang tăng nên ta chọn φ = -π/3

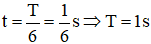
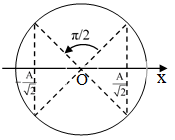
Thời gian đi từ vậy thời gian đi từ x = 5 đến x = 10 là: . Vậy: ω = 2π, f = 1Hz

b) Theo câu a ta có: φ = -π/3.

c) Phương trình dao động: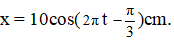

d) Phương trình vận tốc: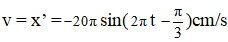

e) Phương trình gia tốc: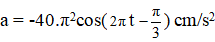

f) Động năng bằng thế năng tại các vị trí:

W = W_đ + W_t = 2W_t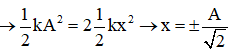

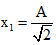
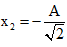
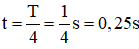
Thời gian để vật đi từ đến là:

Ví dụ 2: Một vật thực hiện đồng thời dao động điều hòa cùng phương, li độ x₁ và x₂ phụ thuộc vào thời gian như hình vẽ. Phương trình dao động tổng hợp là:

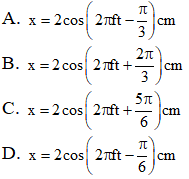
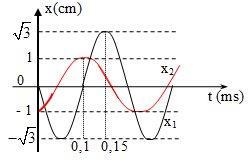
Hướng dẫn:

Từ đồ thị ta có: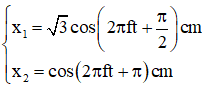

Phương trình dao động tổng hợp ở dạng phức:

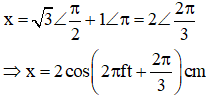
Chọn đáp án B

B. Bài tập trắc nghiệm

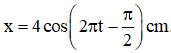
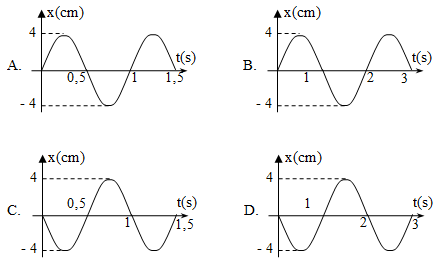
Câu 1. Một vật dao động điều hòa có phương trình . Đồ thị tọa độ - thời gian của vật là hình nào dưới đây?

Lời giải:

Khi t = 0, vật đang đi qua VTCB theo chiều dương.

Chu kì dao động: 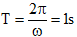. Biên độ: A = 4 cm.

Chọn đáp án A

Câu 2. Cho hai dao động điều hoà, có li độ x₁ và x₂ như hình vẽ. Tổng tốc độ của hai dao động ở cùng một thời điểm có giá trị lớn nhất là:

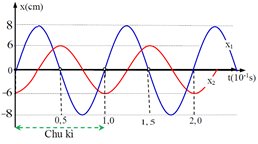
A. 140π cm/s.

B. 100π cm/s.

C. 200π cm/s.

D. 280π cm/s.

Lời giải:

Cách 1: Chu kỳ dao động T = 0,1s. Tần số góc ω = 20π rad/s.

Phương trình dao động của hai vật: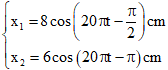

Hai dao động vuông pha nhau nên vận tốc của hai vật cũng vuông pha nhau:

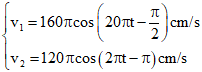
Khi đó: v = v₁ + v₂ = 200πcos(20πt + φ) cm/s. Suy ra: v_max = 200π cm/s.

Chọn đáp án C

Cách 2: Ta có: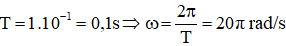

Dao động 1 đang ở vị trí cân bằng và có li độ đang tăng: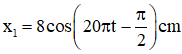

Dao động 2 đang ở vị trí biên âm và đang tăng nên: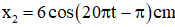

Nhận xét 2 dao động vuông pha nên:

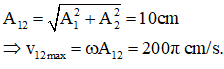
Câu 3. Đồ thị li độ theo thời gian của chất điểm 1 (đường 1) và chất điểm 2 (đường 2) như hình vẽ, tốc độ cực đại của chất điểm 2 là 4π cm/s. Không kể thời điểm t = 0, thời điểm hai chất điểm có cùng li độ lần thứ 5.

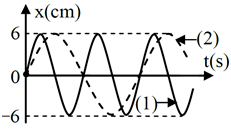
A. 4s.     B. 3,25s.

C. 3,75.     D. 3,5s.

Lời giải:

Cách 1: Ta có: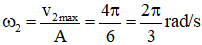

Chu kì chất điểm 2: 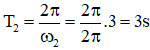. Chu kì chất điểm 1: T₁ = T₂/2 = 1,5s

Phương trình dao động của hai chất điểm: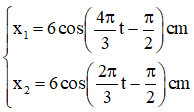

Hai chất điểm có cùng li độ khi:

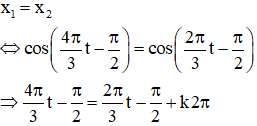
Có hai họ nghiệm t₁ = 3k₁ (s) với k₁ = 1, 2, 3…. Và t₂ = k₂ + 0,5 (s) với k₂ = 0, 1, 2…

Các thời điểm x₁ = x₂:

Chọn đáp án D

Cách 2: Từ hình vẽ ta có: T₂ = 2T₁ → ω₁ = 2ω₂

Mặt khác:

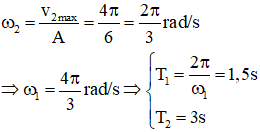
Từ hình vẽ, lần thứ 5 (không kể thời điểm t = 0):

2,25T₁ < t < 2,5T₂ ↔ 3,375s < t < 3,75s.

Chọn đáp án D

Câu 4. Một vật có khối lượng m =100g, đồng thời thực hiện hai dao động điều hòa được mô tả bởi đồ thị hình vẽ. Lực hồi phục cực đại tác dụng lên vật có giá trị là:

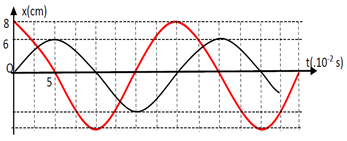
A. 10N     B. 8N

C. 6N     D. 4N

Lời giải:

Từ đồ thị ta có:

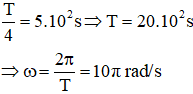
Phương trình dao động của vật có đồ thị x - t (1) và vật có đồ thị x - t (2) là:

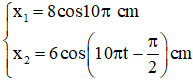
Vì x₁ vuông pha x₂ nên ta có dao động tổng hợp có biên độ:

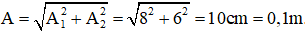
Lực hồi phục cực đại tác dụng lên vật là: F_{hp max} = m.ω².A² = 0,1.(10π)².0,12 = 10N

Chọn đáp án A

Câu 5. Có hai dao động điều hòa (1) và (2) được biểu diễn bằng hai đồ thị như hình vẽ. Đường nét đứt là của dao động (1) và đường nét liền của dao động (2). Hãy xác định độ lệch pha giữa dao động (2) với dao động (1) và chu kì của hai dao động.

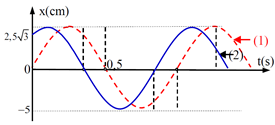
Lời giải:

Lúc t = 0 dao động (1) đang đi qua vị trí cân bằng theo chiều dương nên: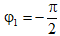

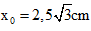
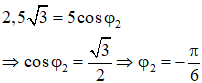
Lúc t = 0 dao động (2) đang đi qua vị trí theo chiều dương nên:

Độ lệch pha của hai dao động: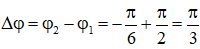

Chu kì: T/2 = 0,5s → T = 1s

Chọn đáp án B

Câu 6. Cho ba vật dao động điều hòa có phương trình dao động lần lượt: x₁ = A₁ cos(ωt + φ₁); x₂ = A₂ cos(ωt + φ₂); x₃ = A₃cos(ωt + φ₃); Biết 3 dao động cùng phương và A₁ = 3A₃; φ₃ – φ₁ = π. Gọi x₁₂ = x₁ + x₂ là dao động tổng hợp của dao động thứ nhất và dao động thứ hai; x₂₃ = x₂ + x₃ là dao động tổng hợp của dao động thứ hai và dao động thứ ba. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ hai dao động tổng hợp trên là như hình vẽ. Giá trị của A₂ gần giá trị nào nhất sau đây?

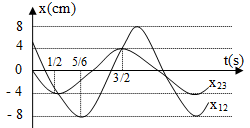
A. 4,36 cm     B. 4,87 cm

C. 4,18 cm     D. 6,93 cm

Lời giải:

Từ đồ thị ta có: T = 2s và x₁₂ trễ hơn x₂₃ một góc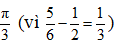

Phương trình của x₁₂ và x₂₃ là:

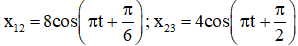
Ngoài ra:

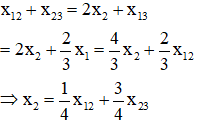
(Vì x₁ ngược pha với x₃ và A₁ > A₃) Bấm máy tính ta được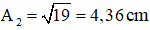

Chọn đáp án B

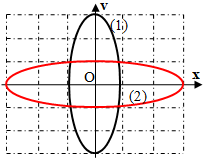
Câu 7. Cho hai vật dao động điều hòa trên hai đường thẳng song song với trục Ox. Vị trí cân bằng của mỗi vật nằm trên đường thẳng vuông góc với ox tại O. Trong hệ trục vuông góc xov, đường (1) là đồ thị biểu diễn mối quan hệ giữa vận tốc và li độ của vật 1, đường (2) là đồ thị biểu diễn mối quan hệ giữa vận tốc và li độ của vật 2 (hình vẽ). Biết các lực kéo về cực đại tác dụng lên hai vật trong quá trình dao động là bằng nhau. Tỉ số giữa khối lượng của vật 2 với khối lượng của vật 1 là

Lời giải:

Cách 1: Nhìn vào đồ thị ta thấy: A₂ = 3A₁

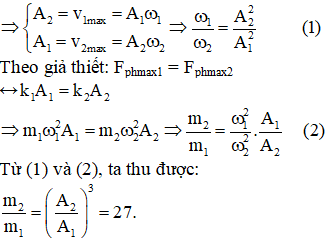
Chọn đáp án C

Cách 2:

Từ đồ thị ta có:

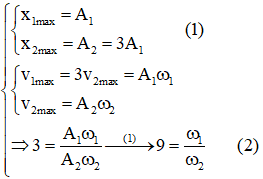
Mặt khác:

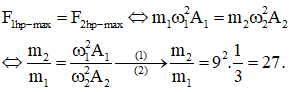
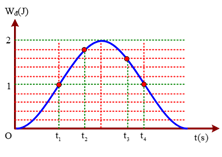
Câu 8. Một con lắc lò xo đang dao động điều hòa. Hình bên là đồ thị biểu diễn sự phụ thuộc của động năng W_đ của con lắc theo thời gian t. Biết t₃ – t₂ = 0,25 s. Giá trị của t4 – t₁ là:

A. 0,54 s.     B. 0,40 s.

C. 0,45 s.     D. 0,50 s.

Lời giải:

Từ đồ thị ta có:

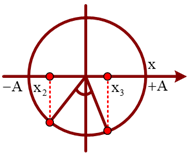
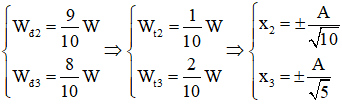
Biểu diễn các vị trí tương ứng trên hình tròn, ta thu được:

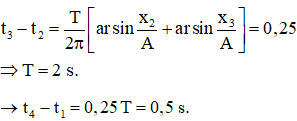
Chọn đáp án: D

Câu 9. Hai chất Hai chất điểm có khối lượng lần lượt là m1, m2 dao động điều hòa cùng phương cùng tần số. Đồ thị biểu diễn động năng của m1 và thế năng của m2 theo li độ như hình vẽ. Tỉ số m1/m2 là:

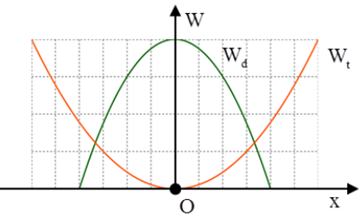
A. 2/3.     B. 9/4.     C. 4/9     D. 3/2.

Lời giải:

Từ đồ thị ta thấy rằng cơ năng của hai vật là như nhau: E₁ = E₂

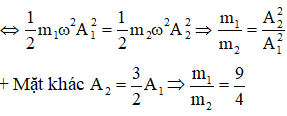
Đáp án B.

Câu 10. Một con lắc lò xo treo vào một điểm cố định, ở nơi có gia tốc trọng trường g = π2 m/s2. Cho con lắc dao động điều hòa theo phương thẳng đứng. Hình bên là đồ thị biểu diễn sự phụ thuộc của thế năng đàn hồi W_đh của lò xo vào thời gian t. Khối lượng của con lắc gần nhất với giá trị nào sau đây

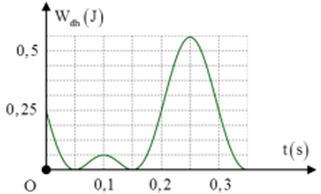
A. 0,45 kg     B. 0,55 kg

C. 0,35 kg     D. 0,65kg

Lời giải:

Thế năng đàn hồi của con lắc lò xo treo thẳng đứng được xác định bởi biểu thức:

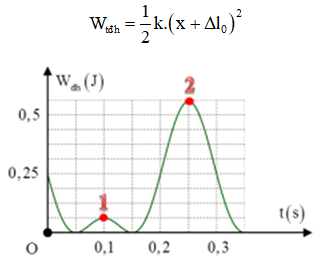
+ Thế năng ở hai vị trí (1) và (2) ứng với:

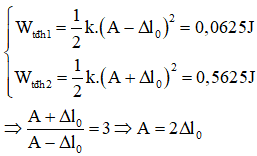
+ Mặc khác, ta để rằng thời gian vật chuyển động từ (1) đến (2) ứng với nửa chu kì T/2 = 0,15 → T = 0,3s.

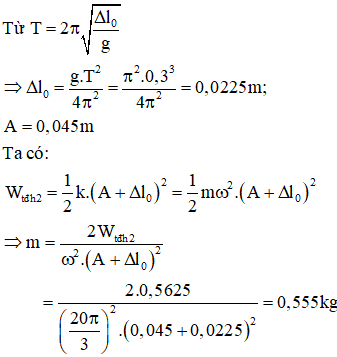
Chọn B

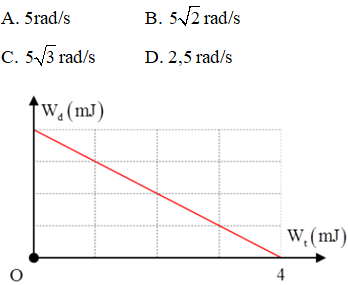
Câu 11. Động năng dao động của một con lắc lò xo được mô tả theo thế năng dao động của nó bằng đồ thị như hình vẽ. Cho biết khối lượng của vật bằng 100 g, vật dao động giữa hai vị trí cách nhau 8cm. Tần số góc của dao động là:

Lời giải:

Từ hình vẽ, ta thấy rằng W = W_tmax = 4mJ.

+ Vật dao động giữa hai vị trí cách nhau 8 cm → A = 4cm

Tần số góc của dao động:

Chọn B.

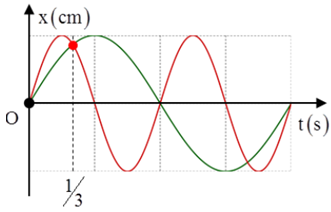
Câu 12. Hai chất điểm dao động điều hòa cùng biên độ có đồ thị biểu diễn li độ theo thời gian như hình vẽ. Tại thời điểm t = 0, hai chất điểm có cùng li độ lần đầu tiên. Tại thời điểm t = 1/3 s, hai chất điểm có cùng li độ lần thứ hai. Thời điểm hai chất điểm có cùng li độ nhưng chuyển động cùng chiều nhau lần thứ hai là

A. 1,5s.     B. 2s.

C. 2,5s.     D. 4s.

Lời giải:

+ Vị trí hai vật có cùng li độ, cùng chiều nhau lần thứ nhất và lần thứ hai được đánh dấu như trên hình vẽ.

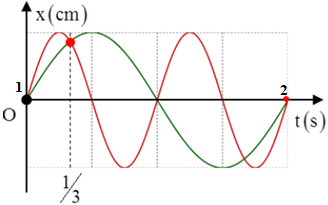
+ Phương trình li độ của hai chất điểm:

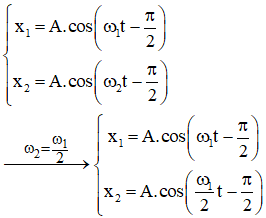
+ Thời điểm hai chất điểm có cùng li độ:

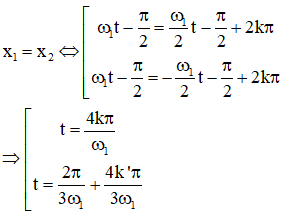
+ Thời điểm hai chất điểm có cùng li độ lần thứ hai ứng với k’ = 0

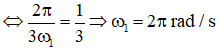
+ Từ hình vẽ ta thấy t₂ = 2T₁ = 2s. Chọn B

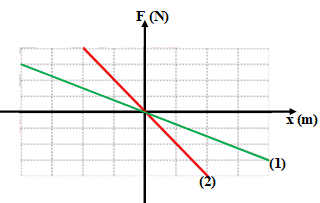
Câu 13. Hai con lắc lò xo dao dộng điều hòa cùng phương, vị trí cân bằng của hai con lắc nằm trên một đường thẳng vuông góc với phương dao động của hai con lắc. Đồ thị lực phục hồi F phụ thuộc vào li độ x của hai con lắc được biểu diễn như hình bên (đường (1) nét liền đậm và đường (2) nét liền mảnh). Chọn mốc thế năng tại vị trí cân bằng. Nếu cơ năng của con lắc (1) là W1 thì cơ năng của con lắc (2) là:

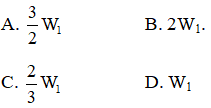
Lời giải:

Từ đồ thị, nếu ta chọn mỗi ô là một đơn vị thì ta có:

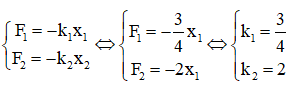
Ta cũng có: A₁ = x_1max = 4; A₂ = x_2max = 2.

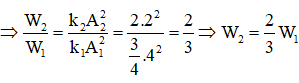
Chọn C

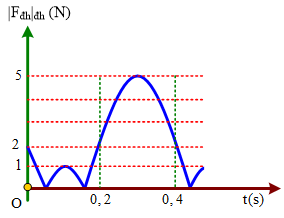
Câu 14. Con lắc lò xo treo thẳng đứng dao động điều hòa ở nơi có gia tốc trọng trường g = π2 m/s2. Độ lớn lực đàn hồi của lò xo biến thiên theo đồ thị như hình vẽ.

Lấy π2 ≈ 10. Khối lượng của vật nhỏ bằng:

A. 100 g.     B. 300 g.

C. 200 g.     D. 400 g

Lời giải:

Trong quá trình dao động của vật, có thời điểm lực đàn hồi có độ lớn bằng 0 → A > Δl₀ (lò xo có cả trạng thái nén và dãn)

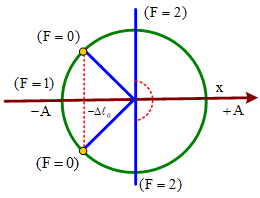
+ Từ đồ thị, ta có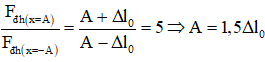

+ Ta để ý rằng, tại thời điểm t = 0 lực đàn hồi có độ lớn đang giảm,

và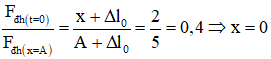

→ tại t = 0 vật chuyển động qua vị trí cân bằng theo chiều âm.

→ Biểu diễn các vị trí tương ứng trên đường tròn, ta dễ dàng thu được

0,5T = 0,4 – 0,2 → T = 0,4 s → ω = 5 rad/s → Δl₀ = 40 cm và A = 60 cm

Ta có: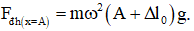

→ Khối lượng của vật nhỏ:

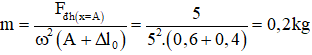
Chọn C.

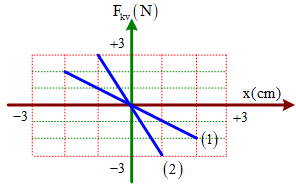
Câu 15. Hai con lắc lò xo nằm ngang dao động điều hòa dọc theo hai đường thẳng song song kề nhau à song song với trục Ox. Hai vật nặng có cùng khối lượng. Vị trí cân bằng của hai dao động đều nằm trên một đường thẳng qua gốc tọa độ và vuông góc với trục Ox. Đồ thị (1), (2) lần lượt biểu diễn mối liên hệ giữa lực kéo về F_kv và li độ x của con lắc 1 và con lắc 2. Biết tại thời điểm t, hai con lắc cùng qua vị trí cân bằng theo cùng một chiều. Sau đó một khoảng thời gian ngắn nhất bằng ∆t_min con lắc 1 có động năng bằng W và bằng một nửa cơ năng của nó, thì thế năng của con lắc 2 khi đó có giá trị gần nhất với giá trị nào sau đây?

A. 1,43 W.     B. 2,36 W.

C. 3,75 W.     D. 0,54 W.

Lời giải:

+ Từ đồ thị, ta thu được: A₁ = 2cm, A₂ = 1cm.

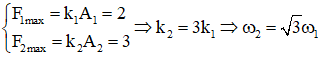
+ Vì hai con lắc cùng khối lượng và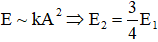

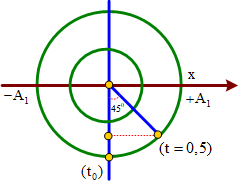
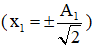
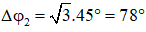
+ Tại t = 0, hai vật đều đi qua vị trí cân bằng, sau khoảng thời gian 0,5 s vật 1 đến vị trí động năng bằng thế năng , tương ứng với góc quét ∆φ₁ = 45º trong khoảng thời gian đó góc quét tương ứng của vật 2 là:

Mặt khác:

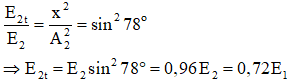
Vì E₁ = 2W (con lắc 1 có động năng bằng W và bằng một nửa cơ năng của nó), nên:

E_2t = 0,72.2.W = 1,44W.

Chọn A.