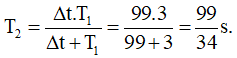Cách giải bài toán Con lắc trùng phùng hay, chi tiết - Vật Lí lớp 12

Cách giải bài toán Con lắc trùng phùng hay, chi tiết

Với Cách giải bài toán Con lắc trùng phùng hay, chi tiết Vật Lí lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Con lắc trùng phùng từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

A. Phương pháp & Ví dụ

1. Phương pháp

♦ Một con lắc đơn A có chu kì T dao động trước mặt một con lắc đồng hồ gõ giây B (chu kì T’ = 2s). Khi hai con lắc cùng đi qua vị trí cân bằng theo cùng một chiều ta bảo hai con lắc trùng phùng. Gọi Δt là thời gian ngăn cách giữa hai lần trùng phùng liên tiếp.

Số dao động mà con lắc B làm được trong thời gian Δt là

Δt = N.T’ = 2N → N = Δt/2

• Nếu T rất gần và nhỏ hơn T’ thì tổng thời gian Δt con lắc A sẽ làm được N + 1 dao động.

• nếu T rất gần và lớn hơn T’ thì trong khoảng thời gian Δt con lắc A sẽ làm được N – 1 dao động

⇒ Ta có hệ thức: Δt = NT’ = ( n ± 1)T

2. Ví dụ

Ví dụ 1: Một con lắc đơn A dao động trước mặt con lắc đồng hồ gõ giây B ( biết T’ = 2s). Thời gian giữa hai lần trùng phùng liên tiếp của con lắc B là 9 phút 50 giây. Tính chu kì T_A của con lắc A biết rằng chu kì cả nó lớn hơn 2 s một chút.

A. 2 s          B. 1,9932 s          C. 2,0068 s          D. 2,01 s

Hướng dẫn:

⇒ Ta có: Δt = 590s→ N_B = Δt/T_B = 590/2 = 295T_A>T_B

⇒ N_A = N_B −1 = 294

⇒ Δt = N_A .T_A = N_B .T_B

⇒ T_A = 590/294 = 2,0068s

Ví dụ 2: Cho con lắc đơn dao động trước mặt một con lắc của đồng hồ gõ giây (có chu kì dao động là 2s). Con lắc đơn dao động chậm hơn con lắc đồng hồ một chút nên có những hai lần con lắc đó chuyển động cùng chiều và đi qua vị trí cân bằng cùng một lúc ( gọi là những lần trùng phùng). Quan sát cho thấy hai lần trùng phùng kế tiếp cách nhau 9 phút 30 giây. Biết chiều dài của con lắc là l = 1m. Hãy xác định gia tốc rơi tự do g tại vị trí đặt của con lắc.

A. 9,874 m/s²          B. 9,811m/s²          C. 9,791m/s²          D. 9,654m/s²

Hướng dẫn:

Vì con lắc đơn dao động chậm hơn con lắc đồng hồ ( nghĩa là trong cùng một khoảng thời gian số dao động của nó nhỏ hơn số dao động của con lắc đồng hồ), cho nên trong khoảng thời gian Δt = 9 phút 30 giây

Vì T > 2 nên Δt = NT = (N + 1)T_o → N = Δt/T_o = ΔT/T – 1 → 1/T = 1/T_o – 1/Δt

→ T = 2,0068 s.

Gia tốc trọng trường tại nơi quan sát:

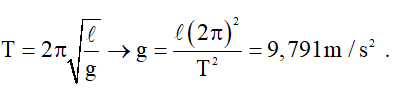
Ví dụ 3: Một con lắc lò xo và một con lắc đơn, khi ở dưới mặt đất cả hai con lắc này cùng dao động với chu kì T = 2s. Đưa cả hai con lắc lên đỉnh núi (coi là nhiệt độ không thay đổi) thì hai con lắc dao động lệch chu kì nhau. Thỉnh thoảng chúng lại cùng đi qua vị trí cân bằng và chuyển động về cùng một phía, thời gian giữa hai lần liên tiếp như vậy là 8 phút 20 giây. Tìm chu kì con lắc đơn tại đỉnh núi đó.

A. 2,010s.          B. 1,992s.          C. 2,008s.          D. 1,008 s.

Hướng dẫn:

Ta biết rằng chu kì dao động của con lắc lò xo phụ thuộc vào m và k chứ không phụ thuộc vào vị trí đặt con lắc, nên khi đưa con lắc từ mặt đất lên đỉnh núi thì chu kì dao động của con lắc lò xo không đổi và chỉ có con lắc đơn là thay đổi.

- Khi đưa con lắc đơn lên đỉnh núi thì chu kì dao động tăng, nghĩa là T > 2 s

- Δt = NT = (N+1)T_o → N = ΔtT = ΔtT_o – 1

→1/T = 1/T_o−1/Δt → T = 2,008s

→ Chọn C.

B. Bài tập trắc nghiệm

Câu 1. Dùng các chớp sáng tuần hoàn chu kỳ 2 s để chiếu sáng một con lắc đơn đang dao động. Ta thấy, con lắc dao động biểu kiến với chu kỳ 30 phút với chiều dao động biểu kiến cùng chiều dao động thật. Chu kỳ dao động thật của con lắc là:

A. 2,005 s     B. 1,978 s      C. 2,001 s     D. 1,998 s

Lời giải:

Chu kì dao đông biểu kiến chính là thời gian “trùng phùng” của hai dao động:

t = nT = (n + 1)T_thật

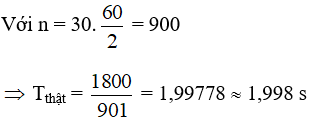
Chọn D

Câu 2. Một con lắc đơn có chu kì dao động T chưa biết dao động trước mặt một con lắc đồng hồ có chu kì T₀ = 2 s. Con lắc đơn dao động chậm hơn con lắc đồng hồ một chút nên có những lần hai con lắc chuyển động cùng chiều và trùng nhau tại vị trí cân bằng của chúng (gọi là những lần trùng phùng). Quan sát cho thấy khoảng thời gian giữa hai lần trùng phùng liên tiếp bằng 7 phút 30 giây. Hãy tính chu kì T của con lắc đơn và độ dài con lắc đơn. Lấy g = 9,8 m/s²

A. 1,98 s và 1 m

B. 2,009 s và 1 m

C. 2,009 s và 2 m

D. 1,98 s và 2 m

Lời giải:

Đối với bài toán con lắc trùng phùng ta có khoảng thời gian giữa 2 lần trùng phùng liên tiếp: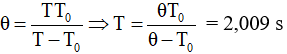, suy ra chiều dài l = 1 m. Chọn B.

Câu 3. Con lắc đơn chu kì T hơi lớn hơn 2s dao động song song trước 1 con lắc đơn gõ giây chu kỳ T₀ = 2s. Thời gian giữa 2 lần trùng phùng thứ nhất và thứ 5 là 28 phút 40 giây. Chu kì T là:

A. 2,015 s     B. 2,009 s     C. 1,995 s      D. 1,002 s

Lời giải:

Cách giải 1:

Thời gian trùng phùng của hai con lắc t = (1/4)(28 phút 40s) = (1/4).1720s = 430 s

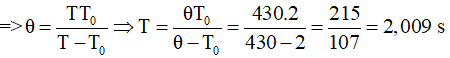
Cách giải 2:

Ta có:

(n + 1)T₀ = nT = 430 ⇒ n = 430/2 – 1 = 214 ⇒ T = 430/n = 430/214 = 2,009 s. Chọn B.

Câu 4. Hai con lắc đơn có cùng khối lượng vật nặng, dao động trong hai mặt phẳng song song cạnh nhau và cùng vị trí cân bằng. Chu kì dao động của con lắc thứ nhất bằng hai lần chu kì dao động của con lắc thứ hai và biên độ dao động của con lắc thứ hai bằng ba lần con lắc thứ nhất. Khi hai con lắc gặp nhau thì con lắc thứ nhất có động năng bằng ba lần thế năng. Tỉ số độ lớn vân tốc của con lắc thứ hai và con lắc thứ nhất khi chúng gặp nhau bằng

A. 4     B. √(14/3)     C. √(140/3)     D. 8

Lời giải:

Coi dao động của các con lắc có biên độ nhỏ: A₁ = l₁.α₁ ; A₂ = l₂.α₂

Do chu kì dao động của con lắc thứ nhất bằng hai lần chu kì dao động của con lắc thứ hai: l₁ = 4.l₂

Do biên độ dao động của con lắc thứ hai bằng ba lần con lắc thứ nhất. A₂ = 3A₁

Hay ta có: l₂.α₂ = 3l₁.α₁ Suy ra α₂ = 12.α₁

Cơ năng dao động của vật 1: E₁ = mgl₁(α₁²)/2

Khi động năng bằng 3 lần thế năng ta có:

E_đ1 = 3/4 E₁ = 3/4 mgl₁.(α₁²)/2 = 3/8 mgl₁.α₁² và li độ góc α = α₁/2

Hai vật gặp nhau ở li độ: S = l₁.α = l₁.α₁/2

Cơ năng dao động của vật 2:

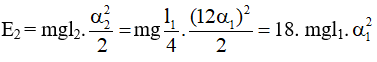
Khi hai vật gặp nhau thế năng vật 2:

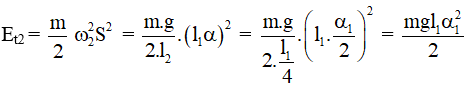
Động năng của vật 2:

E_đ2 = E₂ - E_t2 =

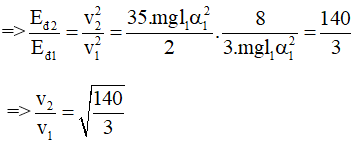
Chọn C

Câu 5. Hai con lắc đơn có chiều dài l₁ = 64 cm; l₂ = 81 cm dao động nhỏ trong hai mặt phẳng song song. Hai con lắc cùng qua vị trí cân bằng và cùng chiều t₀ = 0. Sau thời gian t ngắn nhất hai con lắc trùng phùng (cùng qua vị trí cân bằng, chuyển động cùng chiều). Lấy g = π² (m/s²). Giá trị của t là:

A. 20 s     B. 12 s     C. 8 s     D. 14,4 s

Lời giải:

Hai con lắc có chiều dài l₁ và l₂ dao động với chu kỳ khác nhau, chúng sẽ trùng phùng lần đầu khi một con lắc này dao động hơn con lắc kia đúng 1 chu kỳ. Gọi t là khoảng thời gian gần nhất mà 2 con lắc trùng phùng, n₁ là số chu kỳ vật 1 thực hiện, n₂ là số chu kỳ vật 2 thực hiện. Ta có:

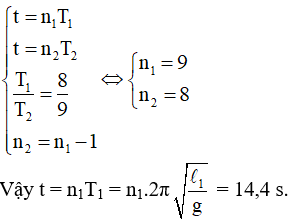
Chọn D

Câu 6. Dùng các chớp sáng tuần hoàn chu kỳ 2s để chiếu sáng một con lắc đơn đang dao động. Ta thấy, con lắc dao động biểu kiến với chu kỳ 30 phút với chiều dao động biểu kiến cùng chiều dao động thật. Chu kỳ dao động thật của con lắc là:

A. 2,005s      B. 1,978s     C. 2,001s      D. 1,998s

Lời giải:

Chu kì dao đông biểu kiến chính là thời gian “trùng phùng” của hai dao động

t = nT = (n+1) T_thật Với n = 30.60/2 = 900 thì T_thật = 1800/901 = 1,99778. Chọn D

Câu 7. Con lắc thứ nhất có chu kỳ T₁ = 3 s, con lắc thứ 2 có chu kỳ T₂. Hai con lắc trùng phùng lần thứ nhất cách nhau 99 s. Tính chu kỳ T₂.

A. 99/34 s     B. 100/33 s

C. 99/31 s     D. 49/24 s

Lời giải:

Hai con lắc trùng phùng lần thứ nhất cách nhau 100 s tức chu kỳ trùng phùng là 100 s.

Ta có: