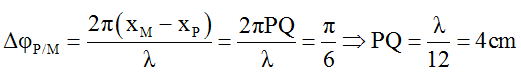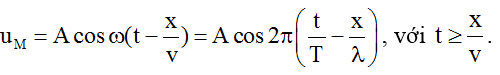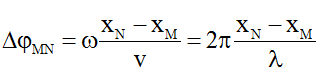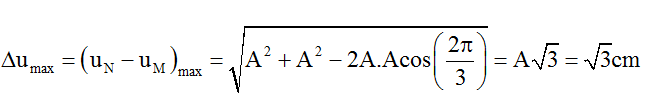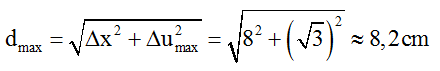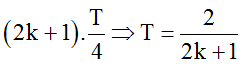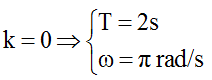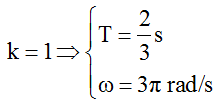Cách giải bài tập về đồ thị sóng cơ cực hay, chi tiết - Vật Lí lớp 12

---

Cách giải bài tập về đồ thị sóng cơ cực hay, chi tiết

Với Cách giải bài tập về đồ thị sóng cơ cực hay, chi tiết Vật Lí lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập đồ thị sóng cơ từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

A. Phương pháp giải

1. Phương trình sóng cơ

+ Tại nguồn O: u_o = A_ocosωt

+ Tại điểm M trên phương truyền sóng: u_M = A_M.cos(ω(t - ∆t))

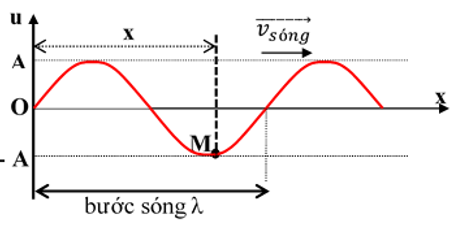
Nếu bỏ qua mất mát năng lượng trong quá trình truyền sóng theo một phương (sống trên sợi dây đàn hồi) thì biên độ sóng tại O và M bằng nhau: A_M = A_o = A.

Ta có:

+ Trường hợp tổng quát

Tại điểm O có phương trình: u_o = Acos(ωt + φ)

Tại điểm M cách O một đoạn x trên phương truyền sóng:

+ Sóng truyền theo chiều dương của trục Ox thì:

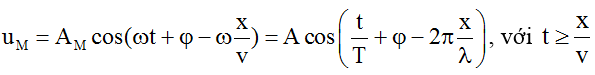
+ Sóng truyền theo chiều âm của trục Ox thì:

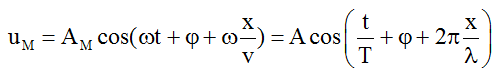
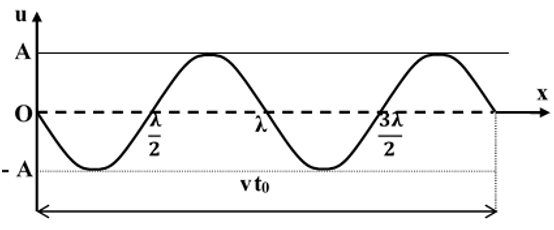
Tại một điểm M xác định trong môi trường sóng: x = const; u_M là hàm điều hòa theo t với chu kỳ T.

Tại một thời điểm xác định t = const; u_M là hàm biến thiên điều hòa theo không gian x với chu kỳ λ.

+ Độ lệch pha giữa hai điểm cách nguồn một khoảng x_M, x_N:

Nếu 2 điểm M và N nằm trên một phương truyền sóng và cách nhau một khoảng x thì: Δφ = ωx/v = 2πx/λ (hoặc nếu 2 điểm M và N trên phương truyền sóng và cách nhau một khoảng d thì Δφ = 2πd/λ )

Khi đó 2 điểm M và N trên phương truyền sóng sẽ:

- dao động cùng pha khi: d = kλ

- dao động ngược pha khi: d = (2k+1)λ/2

- dao động vuông pha khi: d = (2k+1)λ/4

với k = 0; ±1; ±2; ...

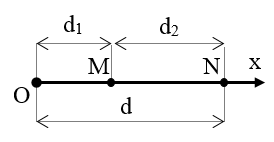
Lưu ý: Đơn vị của x, x₁, x₂, d, λ và v phải tương ứng với nhau.

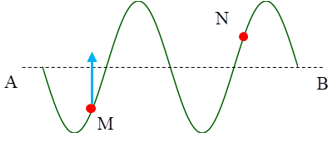
2. Xác định chiều truyền sóng

Cách 1. Ghi nhớ các hình ảnh sau

+ Theo chiều truyền sóng từ trái sang phải:

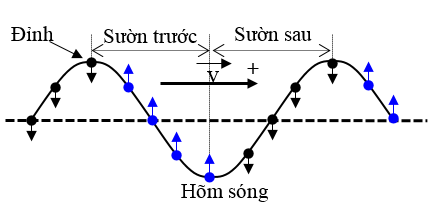
+ Theo chiều truyền sóng từ phải sang trái:

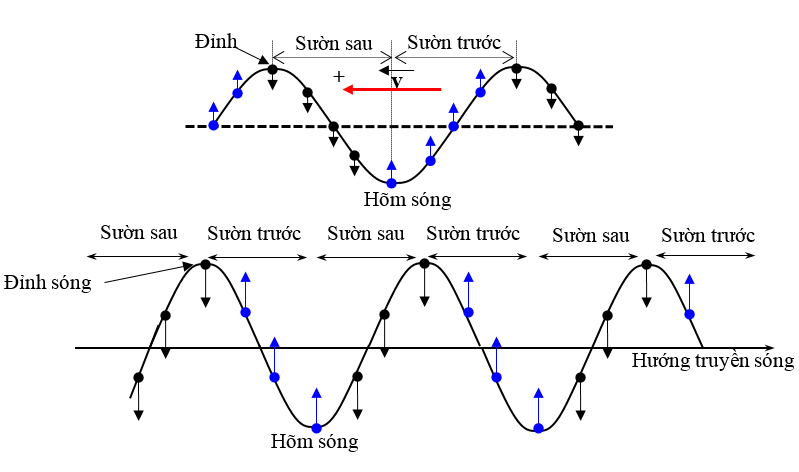
Vậy: khi sóng lan truyền đi: Sườn trước đi lên, Sườn sau đi xuống

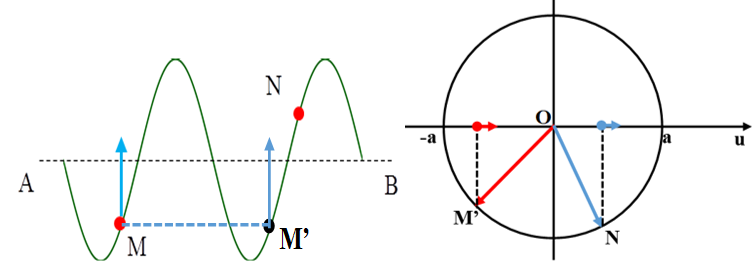
Cách 2. Dựa vào trạng thái dao động của hai điểm M, N trên phương truyền sóng.

Sử dụng vòng tròn lượng giác biểu diễn li độ của các phân tử tại M và N.

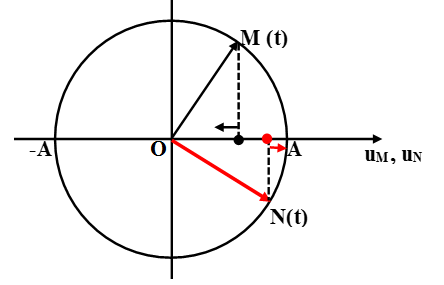
Ta vẽ các vec tơ quay OM, ON biểu thị trạng thái của phần tử sóng tại M và N ở cùng một thời điểm t trên vòng tròn lượng giác.

+ Ví dụ trên hình vẽ phần tử vật chất tại M đang đi xuống (theo chiều âm Ou), phần tử vật chất tại N đang đi lên (theo chiều dương Ou). Như vậy ta thấy OM quay trước ON nên chứng tỏ M sớm pha hơn N, do đó M gần nguồn sóng hơn N. Hay sóng truyền theo chiều từ M đến N.

3. Đọc đồ thị hàm điều hòa:

- Xác định biên độ dựa vào tọa độ đỉnh của đồ thị.

- Xác định pha ban đầu φ: li độ u = u_o khi t = 0 (giao điểm của đồ thị với trục x) sau đó tính cosφ = u_o/A đồng thời quan sát đồ thị đang đi lên thì φ có giá trị âm và ngược lại.

- Xác định khoảng thời gian, thời điểm, chu kỳ (tần số) dựa vào việc chia chu kỳ trên đồ thị.

B. Ví dụ minh họa

Ví dụ 1: (ĐH – 2013): Một sóng hình sin đang truyền trên một sợi dây theo chiều dương của trục Ox. Hình vẽ mô tả hình dạng của sợi dây tại thời điểm t₁ (đường nét đứt) và t₂ = t₁ + 0,3 (s) (đường liền nét).

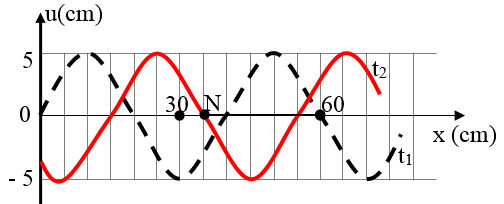
Tại thời điểm t₂, vận tốc của điểm N trên dây là

A. -39,3 cm/s.    B. 65,4 cm/s.    C. -65,4 cm/s.    D. 39,3 cm/s.

Hướng dẫn giải:

Chọn D

Từ hình vẽ ta thấy: Biên độ sóng A = 5 cm.

Từ 30cm đến 60 cm có 6 ô nên chiều dài mỗi ô là: (60-30)/6 = 5cm .

Bước sóng bằng 8 ô nên λ = 8.5 = 40 cm.

Trong thời gian 0,3s sóng truyền đi được 3 ô theo phương ngang tương ứng quãng đường 15 cm nên tốc độ truyền sóng: v = 15/0,3 = 50 cm/s

Chu kì sóng và tần số góc:

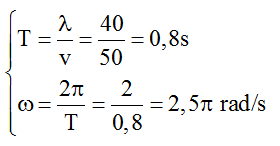
Tại thời điểm t₂, điểm N qua vị trí cân bằng và nằm ở sườn trước nên nó đang đi lên với tốc độ cực đại, tức là vận tốc của nó dương và có độ lớn cực đại:

v_max = ωA = 2,5π.5 ≈ 39,3 cm/s.

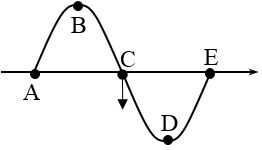
Ví dụ 2: Một sóng cơ truyền trên sợi dây với tần số f = 10 Hz. Tại một thời điểm nào đó sợi dây có dạng như hình vẽ. Trong đó khoảng cách từ vị trí cân bằng của A đến vị trí cân bằng của D là 60 cm và điểm C đang đi xuống qua vị trí cân bằng. Chiều truyền sóng và vận tốc truyền sóng là:

A. Từ E đến A với vận tốc 8 m/s.    B. Từ A đến E với vận tốc 8 m/s.

C. Từ A đến E với vận tốc 6 m/s.    D. Từ E đến A với vận tốc 6 m/s.

Hướng dẫn giải:

Chọn A

Ta có đoạn

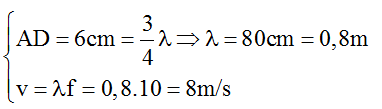
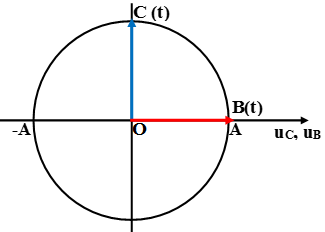
Từ đồ thị ta có: C ở VTCB và đang đi xuống, còn B đang ở vị trí biên dương.

Biểu diễn trên vòng tròn lượng giác ta thấy C nhanh pha hơn B, do vậy C gần nguồn sóng hơn. Vậy sóng truyền từ C đến B, tức là chiều truyền sóng từ E đến A.

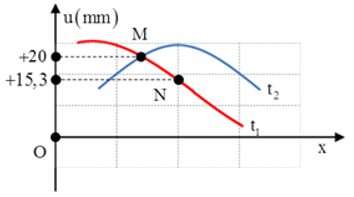
Ví dụ 3: Trên sợi dây dài có sóng ngang hình sin truyền qua. Hình dạng của một đoạn dây tại hai thời điểm t₁ và t₂ có dạng như hình vẽ bên. Trục Ou biểu diễn li độ của các phần tử M và N ở các thời điểm. Biết t₂ – t₁ bằng 0,05 s, nhỏ hơn một chu kì sóng. Tốc độ cực đại của một phần tử trên dây bằng?

A. 34 cm/s.    B. 3,4 m/s.

C. 4,25 m/s.    D. 42,5 cm/s

Hướng dẫn giải:

Chọn A.

Ta biểu diễn li độ sóng tại M, N bằng các vectơ quay trên vòng tròn lượng giác như hình vẽ.

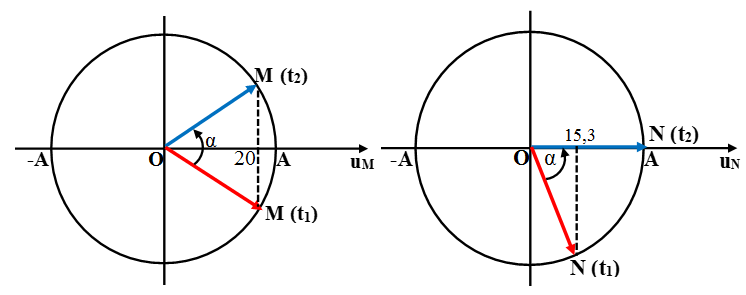
Từ hình vẽ biểu diễn ta xác định được:

+ Tại thời điểm t₁: u_M = 20mm, đang đi lên; u_N = 15,3 mm đang đi lên.

+ Tại thời điểm t₂: u_M = 20mm và đang đi xuống; u_N = +A (tại biên).

Góc quét của vectơ quay biểu diễn M, N từ thời điểm t₁ đến t₂ là bàng nhau và bằng α:

α = (t₂ – t₁).ω.

Ta có:

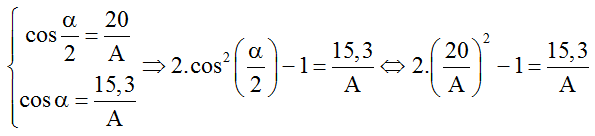
Giải phương trình ta tìm được A = 21,6 mm.

→ α = 0,247π (rad) → ω = 5π rad/s

Suy ra tốc độ cực đại của một phần tử trên dây bằng: V_max = A.ω ≈ 340 mm/s = 34cm/s.

C. Bài tập vận dụng

Câu 1: (Quốc gia – 2017) Trên một sợ dây dài, đang có sóng ngang hình sin truyền qua theo chiều dương của trục Ox. Tại thời điểm t0 một đoạn của sợi dây có hình dạng như hình bên. Hai phần tử M và O dao động lệch pha nhau

A. π/4 rad    B. π/3 rad

C. 3π/4 rad    D. 2π/3 rad

Lời giải:

Chọn B.

+ Từ hình vẽ ta có ∆x = 3 ô đơn vị; λ = 8 ô đơn vị => Δx/λ = 3/8

Vậy độ lệch pha giữa hai điểm O và M sẽ là: Δφ = 2πΔx/λ = 3π/4 rad

Câu 2: Một sóng hình sin đang truyền trên một sợi dây, theo chiều dương của trục Ox. Hình vẽ mô tả hình dạng của sợi dây ở các thời điểm t₁ và t₂ = t₁ + 0,3s. Chu kì của sóng là:

A. 0,9 s    B. 0,4 s

C. 0,6 s    D. 0,8 s

Lời giải:

Chọn D.

Từ đồ thị ta thấy trong khoảng thời gian ∆t = 0,3s, đỉnh sóng đi được quảng đường S = 3 ô đơn vị độ dài = 3.đv (cm)

Vận tốc truyền sóng v = S/∆t = 3.đv/0,3 = 10.đv (cm/s)

Bước sóng của sóng: λ = 8 đơn vị độ dài = 8.đv (cm).

Vậy chu kì của sóng: T = λ/v = 8.đv/(10.dv) = 0,8s.

Câu 3: (Minh họa – 2017) Một sóng hình sin truyền trên một sợ dây dài. Ở thời điểm t, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục Ox. Bước sóng của sóng này bằng

A. 48 cm    B. 18 cm

C. 36 cm    D. 24 cm

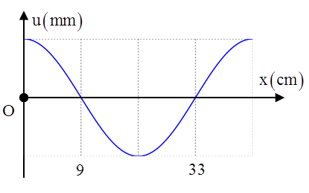
Lời giải:

Chọn A.

Từ hình vẽ ta có λ/2 = 33-9 => λ = 48 cm

Câu 4: Hai điểm A, B cùng phương truyền sóng, cách nhau 25,5cm. Trên đoạn AB có 3 điểm A₁, A₂, A₃ dao động cùng pha với A và 3 điểm B₁, B₂, B₃ dao động cùng pha với B. Sóng truyền theo thứ tự A, B₁, A₁, B₂, A₂, B₃, A₃ và A₃B = 3cm. Tìm bước sóng

A. 6,5cm     B. 7,5cm     C. 5,5cm     D. 4,5cm

Lời giải:

Chọn B

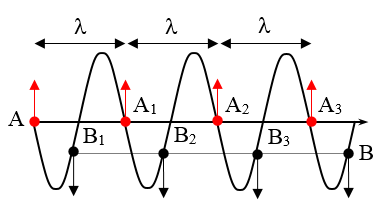
Từ đồ thị ta có: AB = 3λ + A₃B = 3λ + 3 ↔ 25,5 = 3λ + 3 → λ = 7,5cm

Câu 5: Một sóng ngang tần số 100Hz truyền trên một sợi dây nằm ngang với vận tốc 60m/s. M và N là hai điểm trên dây cách nhau 0,75m và sóng truyền theo chiều từ M tới N. Chọn trục biểu diễn li độ cho các điểm có chiều dương hướng lên trên. Tại một thời điểm nào đó M có li độ âm và đang chuyển động đi xuống.

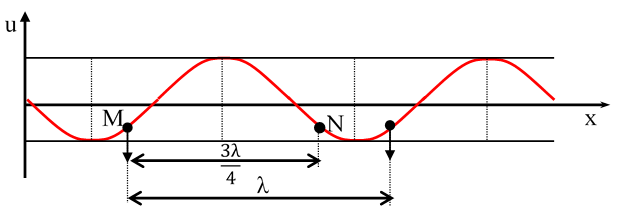
Tại thời điểm đó N sẽ có li độ và chiều chuyển động tương ứng là

A. Âm, đi xuống    B. Âm, đi lên

C. Dương, đi xuống    D. Dương, đi lên

Lời giải:

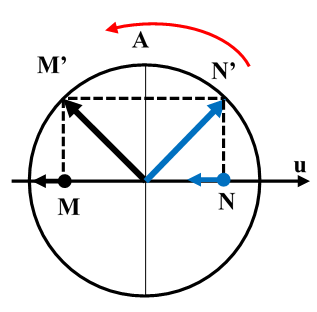
Chọn C

Ta có: λ = v/f = 60/100 = 0,6m

Theo giả thuyết: MN = 0,75 = 0,6 + 0,15 = λ + λ/4

Do sóng truyền từ M đến N nên dao động tại M sớm pha hơn dao động tại N một góc Δφ = 2πd_MN/λ = 5π/2 = 2π + π/2 (vuông pha).

Dùng liên hệ giữa dao động điều hòa và chuyển động tròn đều.

Ta thấy: sóng truyền theo chiều từ M tới N => M nhanh pha hơn N góc π/2. Lúc M có li độ âm và đang chuyển động đi xuống biên âm, thì N sẽ có li độ dương và đi xuống VTCB.

Câu 6: Sóng cơ lan truyền qua điểm M rồi đến điểm N cùng nằm trên một phương truyền sóng cách nhau một phần ba bước sóng. Coi biên độ sóng không đổi bằng A. Tại thời điểm t = 0 có u_M = + 4cm và u_N = - 4cm. Gọi t₁, t₂ là các thời điểm gần nhất để M và N nên đến vị trí cao nhất. Giá trị của t₁, t₂ lần lượt là

A. 5T/12 và T/12 .     B. T/12 và 5T/12 .    C. T/6 và T/12 .    D. T/3 và T/6 .

Lời giải:

Chọn B

Vì u_M = + 4cm và u_N = - 4cm, sóng truyền qua điểm M rồi đến N và M sớm pha hơn N một góc: Δφ = 2πλ/3/λ = 2π/3

=> ta biểu diễn các vectơ quay như hình vẽ:

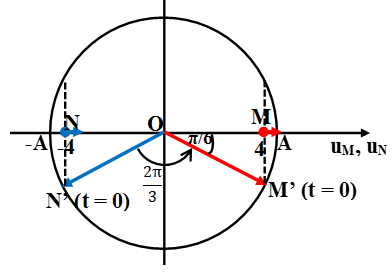
Nhận thấy cả M và N đều đi lên

=> t ngắn nhất để M đi từ vị trí hiện tại đến vị trí cao nhất là t₁ = π/6.T/2π = T/12.

Thời gian ngắn nhất để N đến vị trí cao nhất là: t₂ = (2π/3+ π/6)/2π.T = 5T/12.

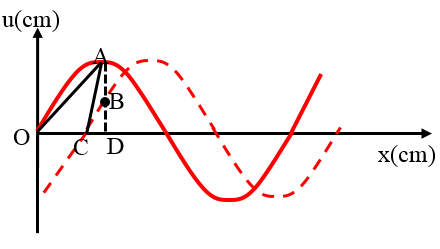
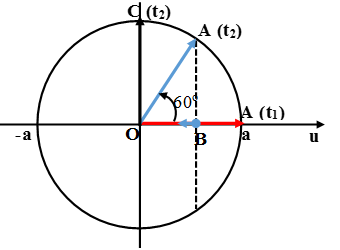
Câu 7: Một sóng cơ lan truyền trên mặt nước dọc theo chiều dương của trục Ox với bước sóng λ , tốc độ truyền sóng là v và biên độ sóng a gắn với trục tọa độ như hình vẽ. Tại thời điểm t₁ sóng có dạng nét liền và tại thời điểm t₂ sóng có dạng nét đứt. Biết AB = BD và vận tốc dao động tại điểm C là v_C = -π/2v. Giá trị của góc ∠OCA .

A. 106,1^o     B. 107,1^o     C. 108,4^o     D. 109,4^o

Lời giải:

Chọn C

Vì AB = BD nên thời gian dao động từ A đến B là t₂ - t₁ = T/6 ứng với sóng truyền từ O đến C với quãng đường OC = λ/6 => CD = λ/4 - λ/6 = λ/12

Vì ở thời điểm t₂ C đang ở VTCB nên nó có tốc độ cực đại:

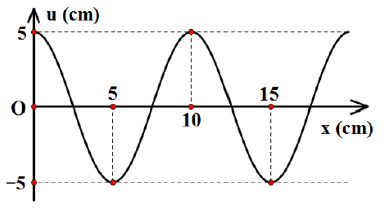
Câu 8: Một sóng cơ truyền trên một sợi dây theo phương ngang, tốc độ truyền sóng là 20 cm/s. Tại thời điểm t = 0 hình dạng của sợi dây được biểu diễn như hình vẽ. Phương trình sóng cơ mô tả hình dáng của sợi dây tại thời điểm t = 2,125 s là:

A. u = 5cos(0,628x + 0,785) cm

B. u = 5cos(0,628x + 1,57) cm

C. u = 5cos(0,628x - 0,785) cm

D. u = 5cos(0,628x -1,57) cm

Lời giải:

Chọn D

Ta có: λ = 10cm → f = v/λ = 2Hz → ω = 4π rad/s

Tại thời điểm t = 2,125 (s) phương trình sóng của sợi dây là:

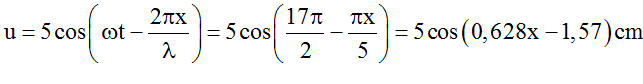
Câu 9: Một sóng truyền theo phương AB. Tại một thời điểm nào đó, hình dạng sóng có dạng như hình vẽ. Biết rằng điểm M đang đi lên vị trí cân bằng. Khi đó điểm N đang chuyển động

A. đi xuống    B. đứng yên

C. chạy ngang    D. đi lên.

Lời giải:

Chọn D

Cách 1: Theo phương truyền sóng, các phần tử trước đỉnh sẽ đi xuống, sau đỉnh sóng sẽ đi lên. Điểm M sau đỉnh sóng đang đi lên vậy sóng truyền từ B đến A và N cũng đang đi lên.

Cách 2:

Xét điểm M’ cách M một khoảng d = λ (như hình vẽ) khi đó M’ cùng trạng thái với M (đang đi lên).

Vì M’ lệch pha với N một góc ∆φ < π, nên ta biểu diễn các vectơ quay như hình vẽ. Ta thấy N sớm pha hơn M’ và đang đi lên.

Câu 10: Một sóng cơ học tại thời điểm t = 0 có đồ thị là đường liền nét. Sau thời gian t, nó có đồ thị là đường đứt nét. Cho biết vận tốc truyền sóng là 4 m/s, sóng truyền từ phải qua trái. Giá trị của t là

A. 0,25 s.    B. 1,25 s.

C. 0,75 s.    D. 2,5 s.

Lời giải:

Chọn C

+ Chọn hai điểm M, N trên phương truyền sóng, cách nhau d = λ/4 như hình vẽ, độ lệch pha của M, N là π/2. Vì sóng truyền từ phải qua trái nên N sớm pha hơn M.

Tại thời điểm t = 0 thì N ở biên dương, M ở VTCB.

Tại thời điểm t, N ở VTCB, M ở biên âm.

Trên vòng tròn lượng giác ta nhận thấy góc quét từ thời điểm t = 0 đến t là 3π/2.

Do đó: t = 3T/4

+ Chu kì của sóng: T = λ/v = 4/4 = 1s => t = 0,75s

Câu 11: (Minh Họa – 2017): Một sóng ngang hình sin truyền trên một sợi dây dài. Hình vẽ bên là hình dạng của một đoạn dây tại một thời điểm xác định. Trong quá trình lan truyền sóng, khoảng cách lớn nhất giữa hai phần tử M và N có giá trị gần nhất với giá trị nào sau đây? Biết biên độ sóng là a = 10mm

A. 8,5 cm.    B. 8,2 cm .

C. 8,35 cm.    D. 8,02 cm.

Lời giải:

Chọn B

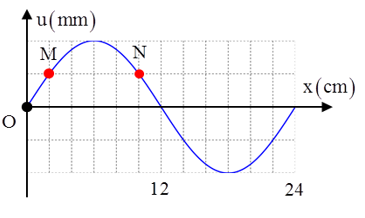
Từ đồ thị ta thấy λ = 24cm, M cách N 1 đoạn d = 4.2 = 8cm

Độ lệch pha dao động giữa hai phần tử M và N

Δφ = 2πΔx/λ = 2π.8/24 = 2π/3 rad

+ Trong hệ tọa độ (uOx), điểm M có tọa độ M(x_M, u_M), điểm N có tọa độ N(x_N, u_N)

Khoảng cách giữa hai chất điểm M, N là:

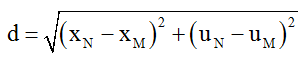
với ∆x = x_N – x_M = 8cm là không đổi, d lớn nhất khi ∆u = u_N - u_M lớn nhất.

Ta có

Vậy

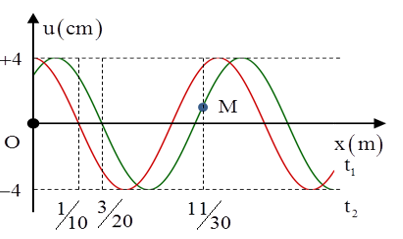
Câu 12: Một sóng hình sin đang truyền trên một sợi dây theo chiều dương của trục 0x. Hình vẽ mô tả hình dạng của sợi dây tại thời điểm t₁ và t₂ = t₁ + 1s. Tại thời điểm t₂, vận tốc của điểm M trên dây gần giá trị nào nhất sau đây?

A. – 3,029 cm/s.    B. – 3,042 cm/s.

C. 3,042 cm/s.    D. 3,029 cm/s.

Lời giải:

Chọn A

Ta có λ/4 = 1/10 => λ = 0,4m

+ Trong 1 s sóng truyền đi được S = 3/20 - 1/10 = 1/20m => v = S/t = 0,05 m/s

Chu kì của sóng T = λ/v = 8s => ω = π/4 rad/s

+ Độ lệch pha dao động theo tọa độ x của M và điểm O

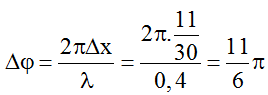
Lưu ý rằng tại thời điểm t₁ M chuyển động theo chiều âm (do nằm trước đỉnh sóng)

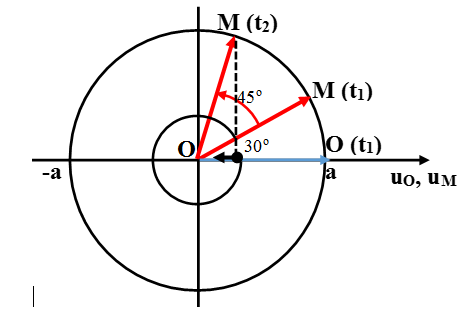
+ Hai thời điểm t₁ và t₂ lệch nhau tương ứng một góc ω.t = π/4 (chú ý rằng M đang chuyển động ngược chiều dương, do vậy li độ điểm M tại thời điểm t₂ là:

u_M = a.cos(45^o + 30^o) = 4.cos75^o (cm)

Vận tốc của M khi đó: v = -v_max.cos15^o = -ωa. cos15^o ≈ -3,029 cm/s

(hoặc sử dụng công thức độc lập để tìm v)

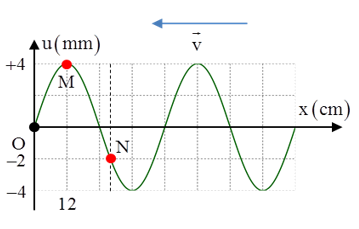
Câu 13: Sóng truyền trên một sợi dây đàn hồi theo ngược chiều dương trục Ox. Tại một thời điểm nào đó thì hình dạng sợi dây được cho như hình vẽ. Các điểm O, M, N nằm trên dây. Chọn đáp án đúng

A. ON = 30cm, N đang đi lên

B. ON = 28cm, N đang đi lên

C. ON = 30cm, N đang đi xuống

D. ON = 28cm, N đang đi xuống

Lời giải:

Chọn D

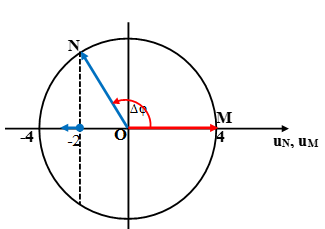
Từ đồ thị ta có: OM = 12cm = λ/4 → λ = 48cm

+ Theo phương truyền sóng, so sánh với đỉnh gần nhất. Trước đỉnh sóng thì phần tử môi trường đi xuống, sau đỉnh sóng thì phần tử môi trường đi lên, suy ra N trước đỉnh M sẽ đi xuống.

(Hoặc sử dụng vòng tròn lượng giác để biểu diễn dao động phần tử sóng tại M, N với điều kiện sóng truyền từ N sang M nên N phải sớm pha hơn M).

+ Từ hình vẽ ta thấy điểm N có li độ u_N = -2 = -A_M/2

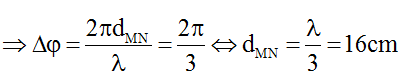
Vậy ON = OM + MN = 12 + 16 = 28cm

Câu 14: Cho một sợi dây cao su căng ngang. Làm cho đầu O của dây dao động theo phương thẳng đứng. Hình vẽ mô tả hình dạng sợi dây tại thời điểm t₁ (đường nét liền) và t₂ = t₁ + 0,2s (đường nét đứt). Tại thời điểm t₃ = t₂ + 0,4s thì độ lớn li độ của phần tử M cách đầu dây một đoạn 4 m (tính theo phương truyền sóng) là √3 cm. Gọi δ là tỉ số của tốc độ cực đại của phần tử trên dây với tốc độ truyền sóng. Giá trị của δ gần giá trị nào nhất sau đây?

A. 0,025    B. 0,018    C. 0,012    D. 0,022

Lời giải:

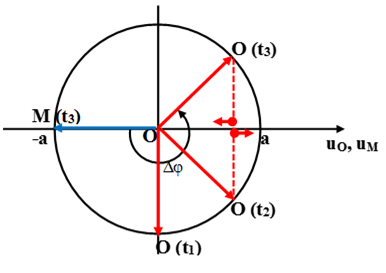
Chọn B

+ Từ đồ thị ta có λ = 6,4m

Vận tốc truyền sóng:

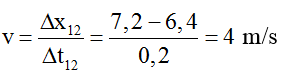
Tần số góc dao động của các phần tử:

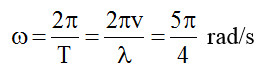
+ Độ lệch pha giữa M và O là:

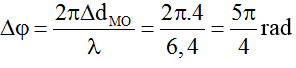
Sử dụng vòng tròn lượng giác ta vẽ các vectơ quay biểu thị dao động của O tại 3 thời điểm t₁, t₂, t₃.

Góc quét từ t₁ đến t₂ là ∆φ1 = (t₂ – t₁).ω = π/4 rad, nên ở thời điểm t₁, O đi qua VTCB theo chiều dương.

Góc quét từ t₂ đến t₃ là ∆φ1 = (t₃ – t₃).ω = π/2 rad.

Vì O nhanh pha hơn M một góc ∆φ = 5π/4 nên ta xác định được ở thời điểm t₃, M ở vị trí biên âm → u_M3 = -a.

Suy ra biên độ sóng:

Vậy tỉ số của tốc độ cực đại của phần tử trên dây với tốc độ truyền sóng:

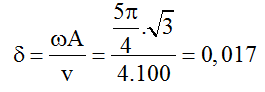
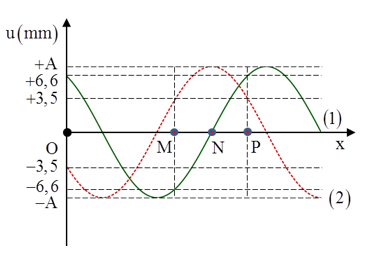
Câu 15: Trên một sợi dây đàn hồi có ba điểm M, N và P, N là trung điểm của đoạn MP. Trên dây có một sóng lan truyền từ M đến P với chu kỳ T (T > 0,5s). Hình vẽ bên mô tả dạng sợi dây tại thời điểm t₁ (đường 1) và t₂ = t₁ + 0,5s (đường 2); M, N và P là vị trí cân bằng của chúng trên dây. Lấy 2√11 = 6,6 và coi biên độ sóng không đổi khi truyền đi. Tại thời điểm t0 = t₁ – 1/9 s, vận tốc dao động của phần tử dây tại N là

A. 3,53 cm/s    B. 4,98 cm/s    C. – 4,98 cm/s    D. – 3,53 cm/s

Lời giải:

Chọn D

+ Ta để ý rằng điểm N tại thời điểm t₁ đang ở vị trí cân bằng, tại thời điểm t₂ N đi đến vị trí biên → t₁ và t₂ là hai thời điểm vuông pha nhau.

Sóng truyền từ M đến P, nên ở thời điểm t₁ N đang đi qua VTCB theo chiều âm (N đi xuống).

Xét điểm P, tại thời điểm t₁ P có li độ u_P1 = 6,6 = 2√11 mm, tại thời điểm t₂, P có li độ u_P2 = 3,5mm.

Ta có hệ thức:

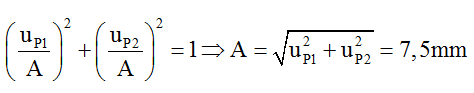
Vì t₁ và t₂ là hai thời điểm vuông pha nhau nên:

∆t = t₂ – t₁ = 0,5s

Vì T < 0,5 s, nên ta có hai trường hợp:

+ Với

Tại thời điểm t₁, phần tử N có vận tốc v = -v_max nên vận tốc của N tại thời điểm t_o = t₁ -1/9 s là: v_N(to) = -ωAcos(ω.1/9) = -22,14 mm/s

+ Với

Vận tốc của phần tử N tại thời điểm t_o = t₁ -1/9 s là: v_N = -ωAcos(ω.1/9) = -35,34 mm/s mm/s.

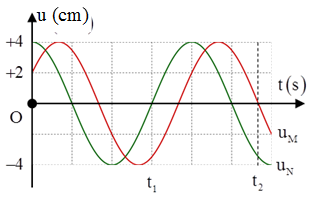
Câu 16: Sóng ngang có tần số f truyền trên một sợi dây đàn hồi rất dài, với tốc độ 3 m/s. Xét hai điểm M và N nằm trên cùng một phương truyền sóng, cách nhau một khoảng x. Đồ thị biểu diễn li độ sóng của M và N cùng theo thời gian t như hình vẽ. Biết t₁ = 0,05 s. Tại thời điểm t₂, khoảng cách giữa hai phần tử chất lỏng tại M và N có giá trị gần giá trị nào nhất sau đây?

A. √19 cm .    B. √20 cm .    C. √23 cm .    D. √18 cm .

Lời giải:

Chọn C

Từ đồ thị ta tìm được phương trình dao động của hai phần tử M, N là:

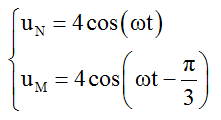
Ta thấy rằng một chu kỳ T chiếm 4 ô đơn vị trên đồ thị, khoảng thời gian t₁ = 0,05s chiếm 3 ô đơn vị, do đó ta có: 3/4T = 0,05 => T = 1/15s => ω = 30π rad/s

Độ lệch pha giữa hai dao động sóng tại M và N là:

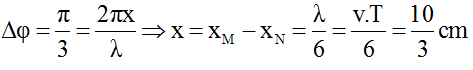
Thời điểm t₂ = T + 5/12T = 17/180s khi đó điểm M đang có li độ u_M = 0 và li độ của điểm N là:

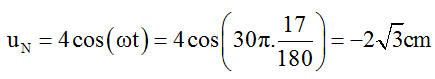
Khoảng cách giữa hai phần tử MN:

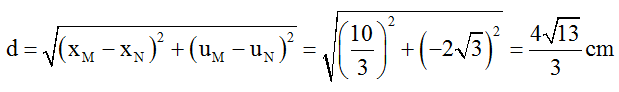
Câu 17: Một sóng cơ lan truyền dọc theo trục Ox với phương trình có dạng u = acos(2π/T.t - 2πx/λ). Trên hình vẽ đường (1) là hình dạng của sóng ở thời điểm t, hình (2) là hình dạng của sóng ở thời điểm trước đó 1/12 s. Phương trình sóng là:

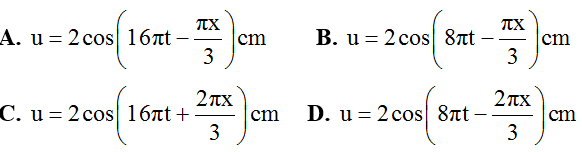
Lời giải:

Chọn A

+ Từ hình vẽ ta xác định được λ = 6cm.

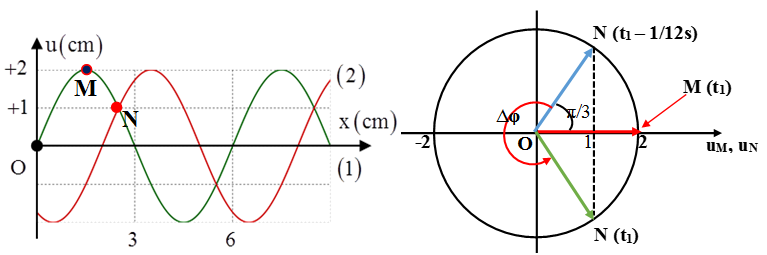
+ Tại cùng một vị trí (xét điểm N) trong không gian, ở hai thời điểm t₁ và t₂ phần tử môi trường tại N đều có li độ là 1 cm nhưng di chuyển theo hai chiều ngược nhau.

Sử dụng vòng tròn lượng giác, ta xác định được ở thời điểm t₁ phần tử N đi lên theo chiều dương (do M sớm pha hơn N).

Từ hình vẽ ta thấy:

∆φ = ωt ⇔ 4π/3 + 2kπ = ω.1/12 => ω = 16π + 24kπ rad/s

Với k = 0 ta được ω = 16π rad/s.

Vậy phương trình dao động sẽ là: u = 2cos(16πt - πx/3) cm

Câu 18: Một nguồn phát sóng cơ hình sin đặt tại O, truyền dọc theo sợi dây đàn hồi căng ngang rất dài OA với bước sóng 48 cm. Tại thời điểm t₁ và t₂ hình dạng của một đoạn dây tương ứng như đường 1 và đường 2 của hình vẽ, trục Ox trùng với vị trí cân bằng của sợi dây, chiều dương trùng với chiều truyền sóng. Trong đó M là điểm cao nhất, u_M, u_N, u_H lần lượt là li độ của các điểm M, N, H. Biết u_M² = u_N² + u_H² và biên độ sóng không đổi. Khoảng cách từ P đến Q bằng

A. 2 cm.    B. 12 cm.    C. 6 cm.    D. 4 cm.

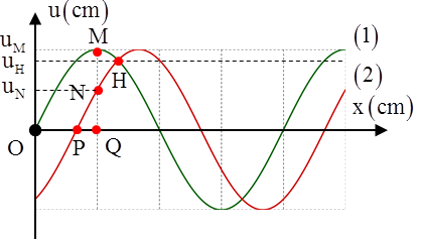
Lời giải:

Chọn D

+ Tại thời điểm t₁, điểm H có li độ u_H và đang tăng, đến thời điểm t₂, điểm H có li độ vẫn là u_H và đang giảm.

+ Phương pháp đường tròn, ta thu được hình vẽ như sau:

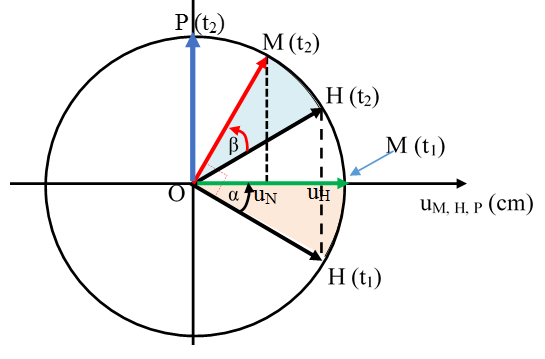
Độ lệch pha của hai dao động tại M và H là không đổi tại mọi thời điểm nên góc quét hợp bởi 2 vectơ quay biểu thị M và H là bằng nhau ở mọi thời điểm → α = β.

Vì u_M² = u_N² + u_H²

=> ∠(M_(t2)OH(_t1))→ α = β = π/6

Vì phần tại tại P dao động sớm pha hơn phần tử tại M nên vectơ quay biểu thị P được vẽ như trên hình. Khi đó độ lệch pha của P so với M là ∆φP/M = π/6.

Mặt khác: