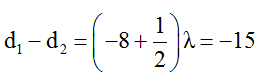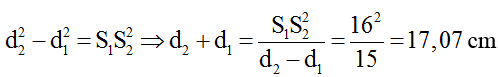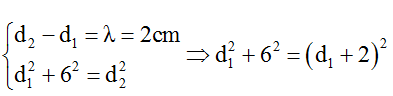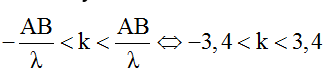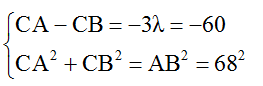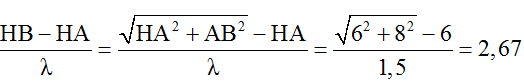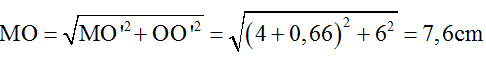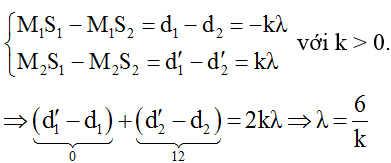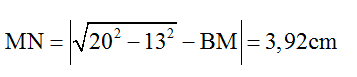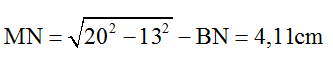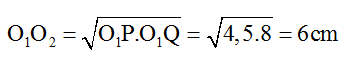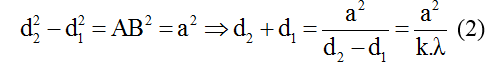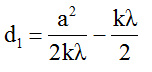Cách giải Bài toán về điểm cực đại, cực tiểu gần nhất, xa nhất với nguồn trong giao thoa sóng hay, chi tiết - Vật Lí lớp 12

Cách giải Bài toán về điểm cực đại, cực tiểu gần nhất, xa nhất với nguồn trong giao thoa sóng hay, chi tiết

Với Cách giải Bài toán về điểm cực đại, cực tiểu gần nhất, xa nhất với nguồn trong giao thoa sóng hay, chi tiết Vật Lí lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập điểm cực đại, cực tiểu gần nhất, xa nhất với nguồn trong giao thoa sóng từ đó đạt điểm cao trong bài thi môn Vật Lí lớp 12.

A. Phương pháp giải

1. Xác định điểm cực đại hoặc cực tiểu nằm trên đường thẳng vuông góc với đoạn nối hai nguồn có khoảng cách gần nhất hoặc xa nhất với đoạn nối 2 nguồn.

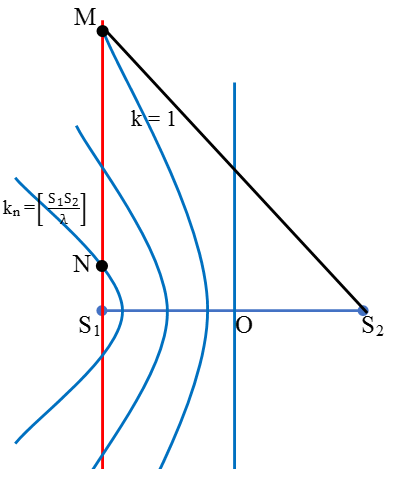
* Xét bài toán tìm trên đường thẳng d vuông góc với 2 nguồn S₁S₂ tại S₁, điểm cực đại cách xa nhất và gần nhất với nguồn S₁ (hoặc tới đoạn thẳng nối 2 nguồn) khi 2 nguồn cùng pha.

Quan sát hình bên ta thấy

+ Điểm cực đại (điểm M trên hình) cách nguồn S₁ xa nhất khi điểm đó nằm trên đường cực đại k = 1. Khi đó ta có:

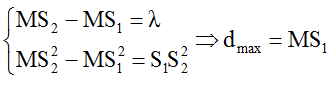
+ Điểm cực đại (điểm N trên hình) cách nguồn S₁ xa nhất khi điểm đó nằm trên đường cực đại ngoài cùng bậc k_n. Khi đó ta có:

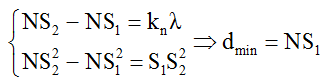
Nếu S₁S₂/λ không nguyên thì ta tìm nhanh k_n = [S₁S₂/λ] .

* Lưu ý:

- Đối với cực tiểu, điểm nằm xa nhất với nguồn khi nằm trên đường k = 0

- Khi 2 nguồn ngược pha ta làm ngược lại.

- Khi 2 nguồn lệch pha bất kỳ ta sử dụng điều kiện cực đại, cực tiểu trong trường hợp hai nguồn lệch pha để tìm vân cực đại, cực tiểu ngoài cùng.

- Phương pháp trên giải quyết cho cả bài toán trong trường hợp điểm cực đại, cực tiểu trên d và cách nguồn S₂ xa nhất và gần nhất.

B. Ví dụ minh họa

Ví dụ 1: Tại mặt chất lỏng có hai nguồn phát sóng kết hợp S₁, S₂ cách nhau 16 cm, dao động điều hòa theo phương vuông góc với mặt chất lỏng với phương trình u₁ = 2cos(40πt) cm và u₂ = 2cos(40πt) cm. Tốc độ truyền sóng trên mặt chất lỏng là 40 cm/s. Gọi M là một điểm thuộc mặt chất lỏng, nằm trên đường thẳng S₁x vuông góc với S₁S₂, cách S₁ một đoạn ngắn nhất mà phần tử chất lỏng tại M dao động với biên độ cực tiểu. Khoảng cách MS₁ bằng

A. 1,42 cm     B. 2,14 cm     C. 2,07 cm     D. 1,03 cm

Hướng dẫn giải:

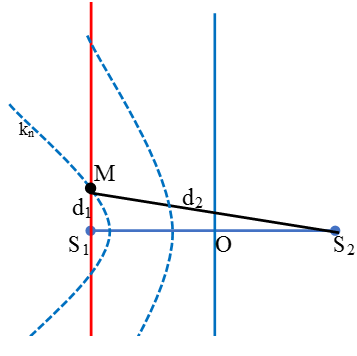
Chọn D.

Bước sóng của sóng λ = v/f = 40/20 = 2cm

Số cực tiểu trên đoạn S₁S₂ được xác đinh như sau:

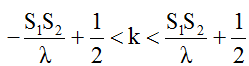
=> -8,5 < k < 7,5

Vì k ϵ Z nên k = -8; -7; ...;-1; 0; 1; ...; 7

Để M cực đại và gần A nhất thì M phải nằm trên hypebol cực tiểu ngoài cùng ứng với kn = -8

Vậy

Kết hợp với

Suy ra d1 = 1,03cm.

2. Xác định điểm cực đại hoặc cực tiểu nằm trên đường tròn, hình vuông, hình chữ nhật... có khoảng cách gần nhất hoặc xa nhất với nguồn, đoạn nối 2 nguồn và đường trung trực của hai nguồn.

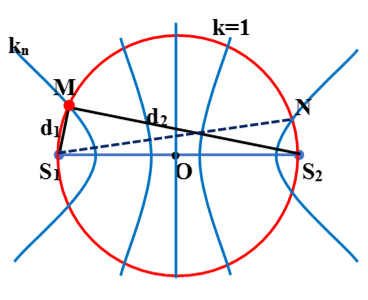
* Xét bài toán tìm trên đường tròn có tâm O là trung điểm của S₁S₂, đường kính S₁S₂ điểm cực đại cách xa nhất và gần nhất với nguồn S₁ (hoặc tới đoạn thẳng nối 2 nguồn) khi 2 nguồn cùng pha.

Quan sát hình bên ta thấy:

+ Điểm cực đại (điểm N trên hình) cách nguồn S₁ xa nhất khi điểm đó nằm trên đường cực ngoài cùng bên phải. Khi đó ta có:

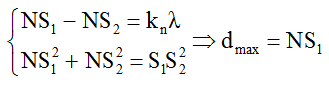
+ Điểm cực đại (điểm M trên hình) cách nguồn S₁ gần nhất khi điểm đó nằm trên đường cực đại ngoài cùng bậc bên trái. Khi đó ta có:

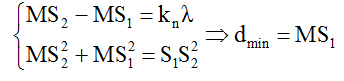
Nếu S₁S₂/λ không nguyên thì ta tìm nhanh k_n = [S₁S₂/λ] .

* Lưu ý:

- Đối với cực tiểu, điểm nằm xa S₁ nhất là thuộc cực tiểu ngoài cùng bên phải, điểm gần S₁ nhất thuộc cực tiểu ngoài cùng bên trái.

- Khi 2 nguồn ngược pha, lệch pha ta cũng làm tương tự nhưng sử dụng điều kiện cực đại, cực tiểu cho trường hợp hai nguồn lệch pha bất kỳ.

- Đối các đường tròn không giống trường hợp trên hoặc các loại hình học khác ta dựa vào tính chất hình học và cách xác định số điểm cực đại, cực tiểu trên một đoạn để xác định được điểm cần tìm nằm ở đường hyperbol nào.

- Trường hợp điểm gần S₂ nhất, xa S₂ nhất ta làm tương tự.

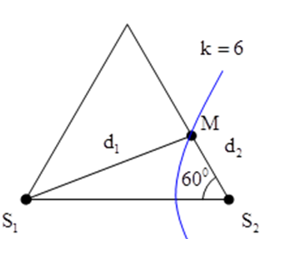
Ví dụ 2: (ĐH – 2013): Trong hiện tượng giao thoa sóng nước, hai nguồn dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 50 Hz được đặt tại hai điểm S₁ và S₂ cách nhau 10 cm. Tốc độ truyền sóng trên mặt nước là 75 cm/s. Xét các điểm trên mặt nước thuộc đường tròn tâm S₁, bán kính S₁S₂, điểm mà phần tử tại đó dao động với biên độ cực đại cách điểm S₂ một đoạn ngắn nhất bằng

A. 85 mm.     B. 15 mm.    C. 10 mm.     D. 89 mm.

Hướng dẫn giải:

Chọn C.

+ Bước sóng của sóng λ = v/f = 1,5cm

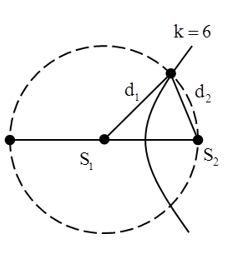
Số điểm dao động với biên độ cực đại trên S₁S₂:

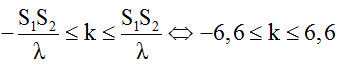
+ Vậy để điểm nằm trên đường tròn dao động cực đại và gần S₂ nhất thì điểm này phải thuộc hyperbol cực đại k = 6.

Từ hình vẽ ta có: d₁ – d₂ = 6λ → d₂ = d₁ - 6λ = S₁S₂ - 6λ = 1cm.

Ví dụ 3: Trong hiện tượng giao thoa sóng hai nguồn kết hợp A, B cách nhau 20 cm dao động điều hoà cùng pha cùng tần số f = 40Hz. Tốc độ truyền sóng trên mặt nước là 1,2m/s. Xét trên đường tròn tâm A bán kính AB, điểm nằm trên đường tròn dao động với biên độ cực đại gần nhất, cách đường trung trực của AB khoảng bằng bao nhiêu ?

A. 27,75 mm     B. 26,1 mm     C. 19,76 mm     D. 32,4mm.

Hướng dẫn giải:

Chọn A.

Bước sóng của sóng: λ = v/f = 3cm.

Số điểm dao động với biên độ cực đại trên AB

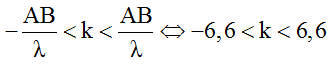
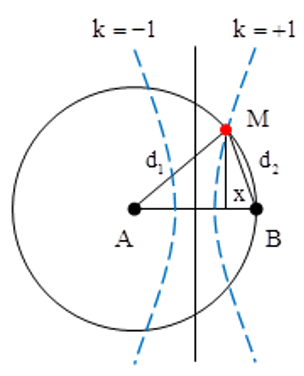
Điểm nằm trên đường tròn dao động với biên độ cực đại và gần trung trực của AB nhất có phải nằm trên các hypebol cực đại ứng với k = 1 hoặc k = -1. Tuy nhiên trong trường hợp này ta thấy rằng điểm này phải nằm trên hypebol k = 1.

→ d₁ – d₂ = λ = 3cm → d₂ = d₁ – 3 = AB – 3 = 17cm.

Từ hình vẽ ta có

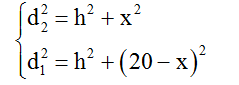
=> d₁² - d₂² = (20-x)² - x²

=> x = 7,225cm

Vậy khoảng cách này sẽ là 10 – x = 2,775cm = 27,75mm.

C. Bài tập vận dụng

Câu 1: Hai nguồn kết hợp A, B đồng bộ cách nhau 6 cm dao động, bước sóng 2 cm. Trên đường thẳng AC vuông góc với AB tại A, người ta thấy điểm M là cực đại nằm xa A nhất và nằm trên đường hypebol ứng với giá trị k (k > 0). Di chuyển nguồn B ra xa dọc theo đường thẳng nối hai nguồn ban đầu, khi đó điểm M tiếp tục nằm trên đường hypebol cực tiểu thứ k + 4. Độ dịch chuyển nguồn B có thể là

A. 8 cm     B. 9 cm     C. 10 cm    D. 12 cm

Lời giải:

Chọn B.

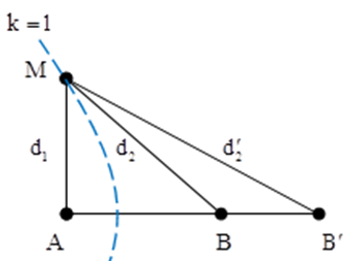
M là cực đại nằm xa A nhất, vậy M là cực đại ứng với k = 1.

Ta có:

Sử dụng máy tính d₁ = 8cm.

Dịch chuyển B đến B’ thì M nằm trên cực tiểu thứ k + 4 = 5, vậy ta có:

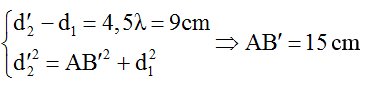
Từ đó ta tìm được BB’ = AB’ – AB = 15 – 6 = 9cm.

Câu 2: (THPTQG – 2015). Tại mặt nước, hai nguồn kết hợp được đặt tại hai điểm A và B cách nhau 68 mm, dao động điều hòa, cùng tần số, cùng pha theo phương vuông góc với mặt nước. Trên AB hai phần tử nước dao động với biên độ cực đại có vị trí cân bằng cách nhau một đoạn ngắn nhất là 10 mm. Điểm C là vị trí cân bằng của một phần tử ở mặt nước sao cho AC vuông góc với BC. Phần tử nước ở C dao động với biên độ cực đại. Khoảng cách BC lớn nhất bằng

A. 37,6 mm.     B. 67,6 mm.     C. 64 mm.    D. 68,5 mm.

Lời giải:

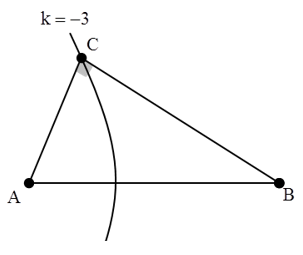
Chọn B.

Khoảng cách gần nhau nhất giữa hai điểm trên AB dao động với biên độ cực đại là λ/2 = 10. Suy ra λ = 20mm.

Số cực đại trên đoạn AB:

Để BC cực đại thì C phải nằm trên hypebol ứng với k = -3.

Từ hình vẽ ta có:

Từ hệ phương trình trên ta thu được: CB = 67,6mm.

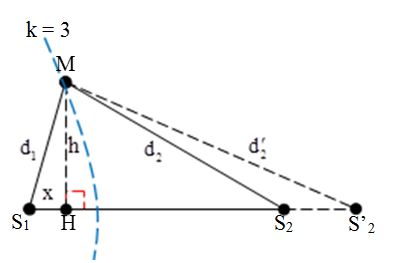
Câu 3: Trên mặt nước có hai nguồn kết hợp A, B cách nhau 8 cm, dao động cùng pha với bước sóng là 1,5 cm. Một đường thẳng xx’ song song với AB cách AB một khoảng 6 cm. M là điểm dao động với biên độ cực đại trên xx’ và gần A nhất. Hỏi M cách trung điểm của AB một đoạn bằng bao nhiêu?

A. 4,66 cm     B. 7,60 cm     C. 4,16 cm     D. 4,76 cm.

Lời giải:

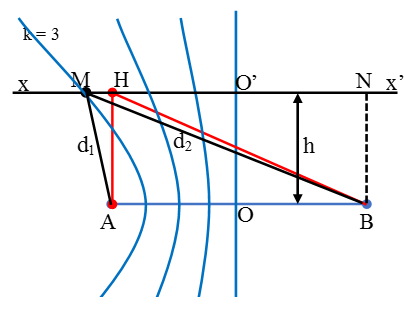
Chọn B.

Số điểm dao động với biên độ cực đại trên đoạn AB:

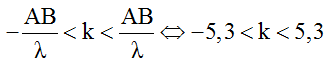
Để M là cực đại và gần A nhất thì M phải nằm trên hypebol ứng bậc k sao cho MH là nhỏ nhất.

Xét tỉ số

→ H gần cực đại thứ 3 nhất do đó M nằm trên hypebol ứng với k = 3.

Ta có d₂ – d₁ = 3.λ = 4,5cm.

Đặt MH = x, từ hình vẽ ta được:

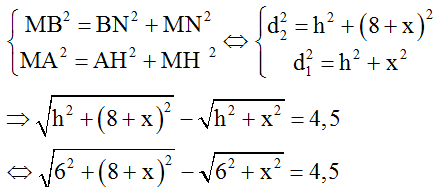
Sử dụng máy tính Casio FX 570VN PLUS ta tìm được x = 0,66cm.

Vậy

Câu 4: Cho hai nguồn sóng kết hợp đồng pha S₁ và S₂ tạo ra hệ giao thoa sóng trên mặt nước. Xét đường tròn tâm S₁ bán kính S₁S₂. M₁ và M₂ lần lượt là các cực đại giao thoa nằm trên đường tròn, xa S₂ và gần S₂ nhất. Biết M1S₂ – M¬2S₂ = 12cm và S₁S₂ = 10 cm. Trên mặt nước có bao nhiêu đường cực tiểu?

A. 4     B. 2    C. 3    D. 5

Lời giải:

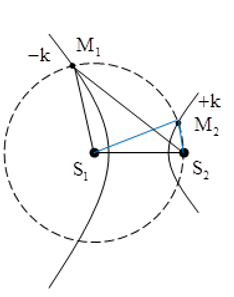
Chọn A.

+ M₁ và M₂ là các điểm cách xa S₂ và gần S₂ nhất nên M1 và M2 nằm trên dãy hypebol ứng với │k│lớn nhất.

+ Ta có

+ Từ đáp áp của bài toán ta thấy số cực tiểu tối đa của 4 đáp án là 5 nên ta xác định được khoảng giá trị của tỉ số S₁S₂/λ là:

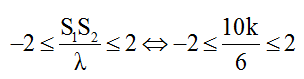
⇔ -1,2 ≤ k ≤ 1,2 => k = 1 => λ = 6cm

Số cực tiểu trên S₁S₂ được xác định như sau:

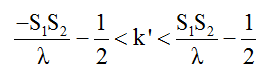
⇔ -2,17 ≤ k ≤ 1,17

Vậy có 4 giá trị k’ nguyên ứng với 4 đường cực tiểu trên mặt nước.

Câu 5: Trong thí nghiệm giao thoa trên mặt nước, hai nguồn sóng kết hợp A và B dao động cùng pha, cùng tần số, cách nhau AB = 8 cm tạo ra hai sóng kết hợp có bước sóng λ = 2cm. Một đường thẳng (∆) song song với AB và cách AB một khoảng là 2cm, cắt đường trung trực của AB tại điểm C. Khoảng cách ngắn nhất từ C đến điểm dao động với biên độ cực tiểu trên (∆) là

A. 0,56 cm.    B. 0,64 cm.     C. 0,43 cm.    D. 0,5 cm.

Lời giải:

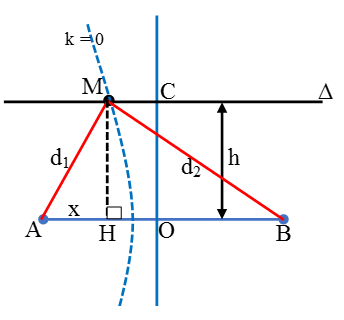
Chọn A.

Để M là cực tiểu và gần trung trực của của AB nhất thì M phải nằm trên cực tiểu ứng với k = 0.

=> d₂ - d₁ = (0 + 1/2)λ = 1cm

Từ hình vẽ, ta có:

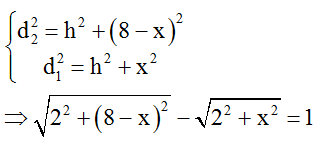
Giải phương trình trên bằng máy tính Casio FX 570VN PLUS ta thu được: x = 3,44cm.

Vậy khoảng cách ngắn nhất giữa M và trung trực AB là 4 – 3,44 = 0,56cm

Câu 6: Tại hai điểm A, B cách nhau 13cm trên mặt nước có hai nguồn phát sóng giống nhau. Cùng dao động theo phương trình u_A = u_B = acos(ωt) cm. Sóng truyền đi trên mặt nước có bước sóng là 2cm, coi biên độ sóng không đổi khi truyền đi. Xét điểm M trên mặt nước thuộc đường thẳng By vuông góc với AB và cách A một khoảng 20cm. Trên By, điểm dao động với biên độ cực đại cách M một khoảng nhỏ nhất bằng:

A. 3,14cm     B. 2,33cm    C. 3,93cm     D. 4,11cm

Lời giải:

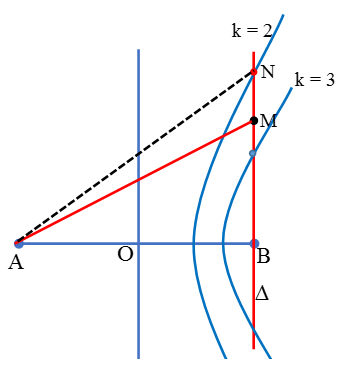
Chọn C.

Số điểm dao động với biên độ cực đại trên AB:

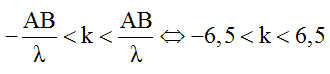
Xét tỉ số:

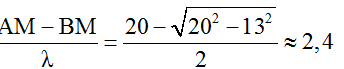
Để N cực đại và gần M nhất thì N phải thuộc cực đại k = 2 hoặc k = 3.

+ Với k = 2

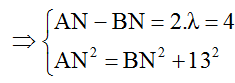
=> (BN+4)² = BN² + 13²

=> BN = 19,125cm

Vậy khoảng cách này sẽ là:

+ Với k = 3

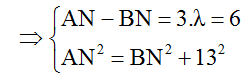
=> (BN+6)² = BN² + 13² => BN = 11,1cm

Vậy khoảng cách này sẽ là

Ta chọn MN_min = 3,92cm.

Câu 7: (Quốc gia – 2013) Trong một thí nghiệm về giao thoa sóng nước, hai nguồn kết hợp O₁ và O₂ dao động cùng pha, cùng biên độ. Chọn hệ trục tọa độ vuông góc xOy thuộc mặt nước với gốc tọa độ là vị trí đặt nguồn O₁ còn nguồn O₂ nằm trên trục Oy. Hai điểm P và Q nằm trên Ox có OP = 4,5 cm và OQ = 8 cm. Dịch chuyển nguồn O₂ trên trục Oy đến vị trí sao cho góc PO₂Q có giá trị lớn nhất thì phần tử nước tại P không dao động còn phần tử nước tại Q dao động với biên độ cực đại. Biết giữa P và Q không còn cực đại nào khác. Trên đoạn OP, điểm gần P nhất mà các phần tử nước dao động với biên độ cực đại cách P một đoạn là:

A. 3,4 cm.     B. 2,0 cm .     C. 2,5 cm .     D. 1,1 cm.

Lời giải:

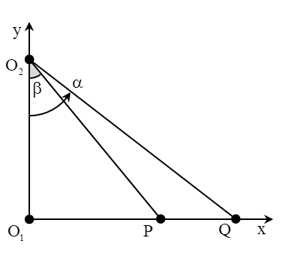
Chọn B.

+ Từ hình vẽ ta có:

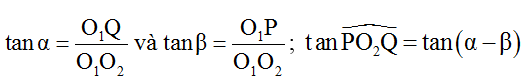
+ Biến đổi lượng giác:

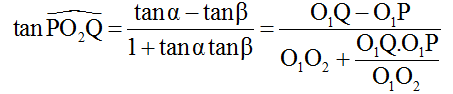
+ Để ∠PO₂Q lớn nhất thì

Khi đó P cực tiểu, Q cực đại và giữa P và Q không có cực đại nào khác, suy ra:

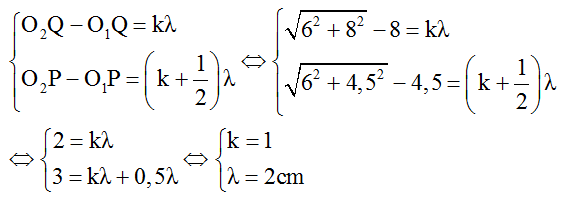
+ Trên đoạn OP, điểm M gần P nhất dao động cực đại sẽ nằm trên hypebol ứng với k = 2.

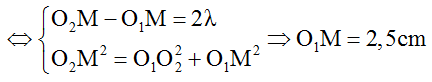
Vậy khoảng cách giữa M và P là 4,5 – 2,5 = 2 cm.

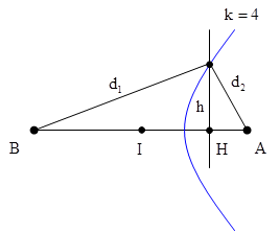
Câu 8: Hai nguồn A, B cùng biên độ, cùng pha, cùng tần số 50Hz, AB = 20cm. Tốc độ truyền sóng trên mặt nước là 1,5m/s. Xét trên đường thẳng xy vuông góc với AB, cách trung trực của AB là 7cm; điểm dao động cực đại trên xy gần A nhất; cách A là:

A. 8,75cm.     B. 14,46cm    C. 10,64cm    D. 5,67cm

Lời giải:

Chọn D

+ Bước sóng của sóng λ = v/f = 3cm.

+ Xét tỉ số 2IH/λ = 4,67

Suy ra điểm dao động với biên độ cực đại gần A nhất trên xy phải thuộc hypebol k = 4.

+ Từ hình vẽ ta có:

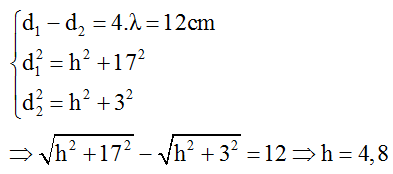
Từ đó ta tìm được

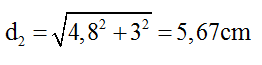
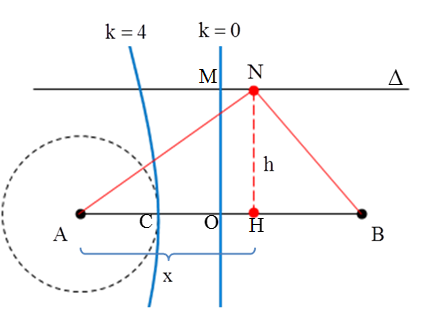
Câu 9: Trong thí nghiệm giao thoa sóng mặt nước, hai nguồn kết hợp A, B cách nhau 8 cm dao động cùng pha. Ở mặt nước, có 21 đường dao động với biên độ cực đại và trên đường tròn tâm A bán kính 2,5 cm có 13 phần tử sóng dao động với biên độ cực đại. Đường thẳng (∆) trên mặt nước song song với AB và cách đường thẳng AB một đoạn 5 cm. Đường trung trực của AB trên mặt nước cắt đường thẳng (∆) tại M. Điểm N nằm trên (∆) dao động với biên độ cực tiểu gần M nhất cách M một đoạn d. Giá trị d gần nhất với giá trị nào sau đây?

A. 0,20 cm.    B. 0,36 cm.    C. 0,48 cm.     D. 0,32 cm.

Lời giải:

Chọn D

+ Trên mặt nước có 21 dãy cực đại, như vậy nếu không tính trung trực của AB thì từ H đến A có 10 dãy cực đại.

+ Mặc khác trên đường tròn tâm A bán kính 2,5 cm lại có 13 cực đại điều này chứng tỏ trong đường tròn chứa 6 cực đại (cắt đường tròn tại 12 điểm) và giao điểm giữa đường tròn và AB là một cực đại.

+ Trên đoạn OC các cực đại cách đều nhau nửa bước sóng.

=> OC = 4 λ/2 = 4 - 2,5 => λ = 0,75.

+ Để N gần M nhất thì N thuộc cực tiểu thứ nhất, từ hình vẽ, ta có:

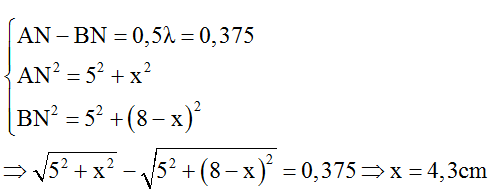
Vậy MN = AH – AO = x – AO = 4,3 – 4 = 0,3cm.

Câu 10: Trong hiện tượng giao thoa sóng nước, hai nguồn S₁ và S₂ dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 50 Hz được đặt tại hai điểm cách nhau 10 cm. Tốc độ truyền sóng trên mặt nước là 75 cm/s. C là một điểm trên mặt nước có CS₁ = CS₂ = 10cm. Xét các điểm trên mặt nước thuộc đoạn thẳng CS₂, điểm mà phần tử tại đó dao động với biên độ cực đại các S₂ một đoạn ngắn nhất có giá trị gần nhất giá trị nào sau đây?

A. 4mm    B. 7mm    C. 9mm    D. 5mm

Lời giải:

Chọn D

Số cực đại giao thoa trên đoạn thẳng nối hai nguồn:

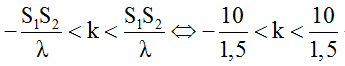
⇔ -6,3 < k < 6,3

Để M là một điểm trên CS₂ cực đại và gần S₂ nhất thì M phải nằm trên hypebol cực đại bậc 6.

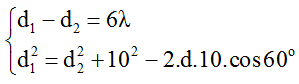
=> (d₂+9)² = d₂² - 10d₂ + 100

=> d = 6,7 mm

Câu 11: Tại mặt nước có hai nguồn kết hợp S₁ và S₂ cách nhau 12 cm, dao động đồng phau nhau với tần số 20 Hz. Điểm M cách S₁S₂ lần lượt 4,2 cm và 9 cm. Biết tốc độ truyền sóng trên mặt nước là 32 cm/s. Để điểm M thuộc vân cực tiểu thì phải dịch chuyển S₂ theo phương S₁S₂ ra xa S₁ một khoảng tối thiểu bằng

A. 1,62 cm    B. 4,80 cm    C. 0,83 cm    D. 0,54 cm

Lời giải:

Chọn C

Bước sóng: λ = v/f = 32/20 = 1,6cm.

Xét tỉ số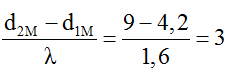

Vậy ban đầu điểm M nằm trên cực đại bậc 3.

Ta có: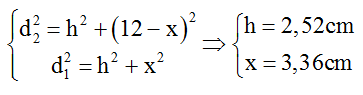

Dịch chuyển S₂ ra xa một đoạn Δd, để đoạn này là nhỏ nhất thì khi đó M phải nằm trên cực tiểu thứ 4.

Ta có d'₂ - d₁ = 3,5λ => d'₂ = 9,8 cm

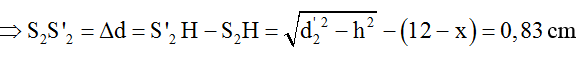
Câu 12: Trên mặt thoáng của một chất lỏng có hai nguồn sóng A, B cách nhau 10 cm, dao động cùng pha, cùng tần số f =15Hz. Gọi ∆ là đường trung trực của AB. Xét trên đường tròn đường kính AB, điểm mà phần tử ở đó dao động với biên độ cực đại cách ∆ một khoảng nhỏ nhất là 1,4 cm. Tốc độ truyền sóng trên mặt chất lỏng là

A. 0,42 m/s    B. 0,84 m/s    C. 0,30 m/s    D. 0,60 m/s

Lời giải:

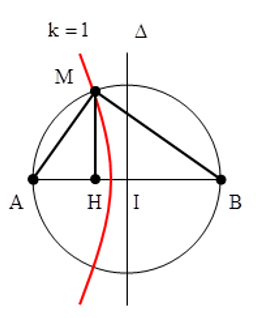
Chọn C

Để IH là nhỏ nhất thì M nằm trên hypebol cực đại bậc 1.

Từ hình vẽ ta có: AH = 3,6cm; BH = 6,4cm.

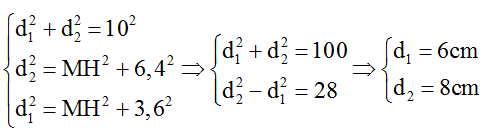
Mặt khác: d₂ - d₁ = λ = v/f ⇔ 8 - 6 = v/15 => v = 0,3 m/s

Câu 13: (QG – 2016) Ở mặt chất lỏng có hai nguồn kết hợp đặt tại A và B dao động điều hòa, cùng pha theo phương thẳng đứng. Ax là nửa đường thẳng nằm ở mặt chất lỏng và vuông góc với AB. Trên Ax có những điểm mà các phần tử tại đó dao động với biên độ cực đại, trong đó M là điểm xa A nhất, N là điểm kế tiếp với M, P là điểm kế tiếp với N và Q là điểm gần A nhất. Biết MN = 22,25cm, NP = 8,75cm. Độ dài đoạn QA gần nhất với giá trị nào sau đây?

A. 1,2 cm.     B. 4,2 cm.     C. 2,1 cm.     D. 3,1 cm.

Lời giải:

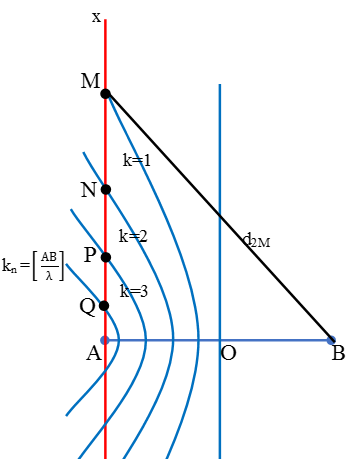
Chọn C.

+ Quy luật về khoảng cách d₁ của các điểm dao động cực đại trên Ax.

Để M dao động với biên độ cực đại thì d₂ – d₁ = kλ. (1)

+ Mặc khác

Từ (1) và (2) ta thu được:

→ Áp dụng cho bài toán cho các điểm M, N, P:

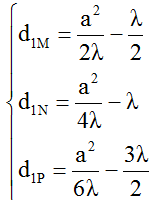
+ Từ đó ta thu được hệ phương trình sau:

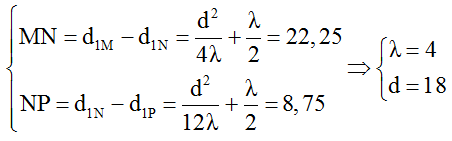
→ Q là điểm cực đại gần A nhất nên Q thuộc cực đại ngoài cùng với k = [AB/λ] = 4

=> QA = d_1Q = d²/8λ - 2λ = 2,125cm.

Câu 14: Trên bề mặt một chất lỏng, tại hai điểm A, B cách nhau 14 cm có hai nguồn dao động điều hòa theo phương thẳng đứng với cùng biên độ, cùng tần số và cùng pha tạo ra hai sóng kết hợp có bước sóng bằng 4 cm. C là một điểm trên mặt chất lỏng sao cho tam giác ABC vuông cân tại C. Trên đoạn AC, hai điểm liên tiếp có phần tử sóng dao động với biên độ cực đại cách nhau một đoạn ngắn nhất xấp xỉ bằng bao nhiêu?

A. 3,687 cm.     B. 1,817 cm.     C. 3,849 cm.     D. 2,500 cm.

Lời giải:

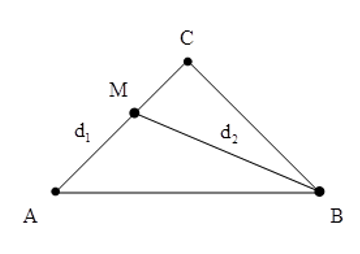
Chọn D.

Số điểm dao động với biên độ cực đại trên AB:

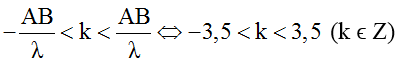
Suy ra có 7 điểm dao động với biên độ cực đại

Gọi M là một điểm thuộc cực đại bậc k trên AC, ta có:

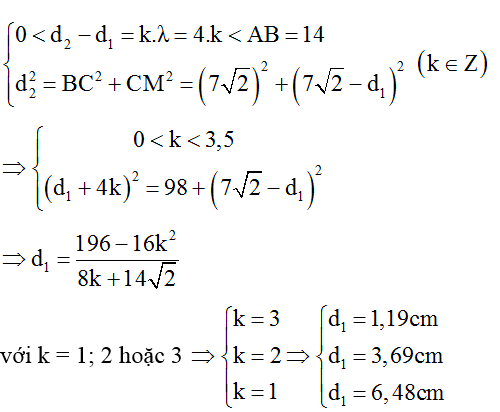
Vậy khoảng cách ngắn nhất cần tìm là: ∆d_min = 3,69 – 1,19 = 2,5cm.