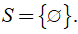Lý thuyết Mở đầu về phương trình hay, chi tiết

Lý thuyết Mở đầu về phương trình hay, chi tiết

Haylamdo biên soạn và sưu tầm Lý thuyết Mở đầu về phương trình hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Lý thuyết

1. Phương trình một ẩn

+ Một phương trình với ẩn x là hệ thức có dạng A( x ) = B( x ), trong đó A( x ) gọi là vế trái, B( x ) gọi là vế phải.

+ Nghiệm của phương trình là giá trị của ẩn x thoả mãn (hay nghiệm đúng) phương trình.

Chú ý:

Hệ thức x = m (với m là một số nào đó) cũng là một phương trình. Phương trình này chỉ rõ rằng m là nghiệm duy nhất của nó.

Một phương trình có thể có một nghiệm, hai nghiệm, ba nghiệm,….nhưng cũng có thể không có nghiệm nào hoặc có vô số nghiệm. Phương trình không có nghiệm nào được gọi là phương trình vô nghiệm.

Ví dụ 1:

3x + 2 = 2x là phương trình với ẩn x.

2y - 1 = 4( 1 - y ) + 3 là phương trình với ẩn y.

Ví dụ 2:

Phương trình x² = 1 có hai nghiệm x = 1 và x = - 1.

Phương trình x² = - 1 vô nghiệm

2. Giải phương trình

+ Giải phương trình là tìm tất cả các nghiệm của phương trình.

+ Tìm tập hợp tất cả các nghiệm của một phương trình được gọi là tập nghiệm của phương trình đó. Tập hợp các nghiệm của phương trình kí hiệu là S.

Ví dụ:

Phương trình x = 3 có tập nghiệm là S = { 3 }.

Phương trình vô nghiệm có tập nghiệm là

3. Phương trình tương đương.

Hai phương trình tương đương nếu chúng có cùng một tập hợp nghiệm.

Kí hiệu ⇔ đọc là tương đương.

Ví dụ:

x + 3 = 0 ⇔ x = -3.

x - 1 = 3 ⇔ x = 4.

B. Bài tập tự luyện

Bài 1: Tìm tập nghiệm của các phương trình sau đây?

a) - 3x = - 7/2

b) 2x = 6.

c) - 5/2x = - 5.

Hướng dẫn:

a) Ta có: - 3x = - 7/2 ⇔ x = ( - 7/2)/ - 3 = 7/6.

Vậy tập nghiệm của phương trình là S = { 7/6 }

b) Ta có: 2x = 6 ⇔ x = 6/2 ⇔ x = 3.

Vậy phương trình có tập nghiệm là S = { 3 }

c) Ta có: (-5/2)x = - 5 ⇔ x = - 5/(-5/2) ⇔ x = 2.

Vậy tập nghiệm của phương trình là S = {2}

Bài 2: Chứng minh rằng các phương trình sau tương đương

a) 2x = 6 và 1,5x = 4,5.

b) - 2x = 4 và x/2 = - 1

Hướng dẫn:

a) Ta có:

+ Phương trình 2x = 6 ⇔ x = 3 có tập nghiệm là S = { 3 }

+ Phương trình 1,5x = 4,5 ⇔ x = 4,5/1,5 ⇔ x = 3 có tập nghiệm là S = { 3 }

→ Hai phương trình có cùng tập nghiệm.

→ Hai phương trình tương đương.

b) Ta có:

+ Phương trình - 2x = 4 ⇔ x = - 2 có tập nghiệm là S = {- 2}

+ Phương trình x/2 = - 1 ⇔ x = - 2 có tập nghiệm là S = {- 2}

→ Hai phương trình có cùng tập nghiệm.

→ Hai phương trình tương đương.