Tìm giá trị lớn nhất, giá trị nhỏ nhất của diện tích một hình

Tìm giá trị lớn nhất, giá trị nhỏ nhất của diện tích một hình

Tài liệu Tìm giá trị lớn nhất, giá trị nhỏ nhất của diện tích một hình Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Tìm giá trị lớn nhất (nhỏ nhất) của diện tích một hình

A. Phương pháp giải

+) Nếu diện tích của một hình luôn lớn hơn hoặc bằng một hằng số m, và tồn tại một vị trí của hình để diện tích bằng m thì m là số đo diện tích nhỏ nhất của hình đó.

+) Nếu diện tích của một hình luôn nhỏ hơn hoặc bằng một hằng số M, và tồn tại một vị trí của hình để diện tích bằng M thì M là số đo diện tích lớn nhất của hình đó.

B. Ví dụ minh họa

Câu 1: Trong các hình chữ nhật có cùng chu vi là 100cm, hình có diện tích lớn nhất là bao nhiêu?

Lời giải:

Nửa chu vi của hình chữ nhật là: 100:2 = 50cm

Gọi kích thước của hình chữ nhật là x (cm; x>0) thì kích thước còn lại là 50-x (cm)

Diện tích hình chữ nhật là:

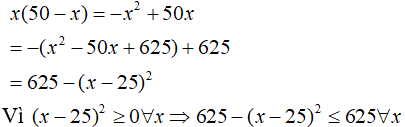
Dấu “=” xảy ra khi x = 25.

Vậy hình chữ nhật có diện tích lớn nhất là 25² = 625(cm²).

Câu 2: Cho đoạn thẳng AB có độ dài 2a. Vẽ về một phía của AB các tia Ax và By vuông góc với AB. Qua trung điểm M của AB có hai đường thẳng thay đổi luôn vuông góc với nhau và cắt Ax, By theo thứ tự tại C và D. Xác định vị trí của các điểm C, D sao cho tam giác MCD có diện tích nhỏ nhất. Tính diện tích tam giác đó?

Lời giải:

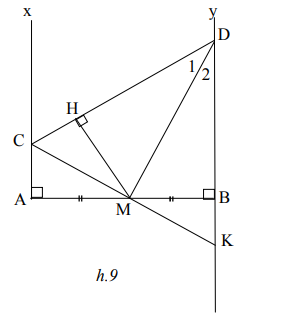
Lời giải:

Gọi K là giao điểm của CM và DB.

Xét ΔAMC và ΔBMK có:

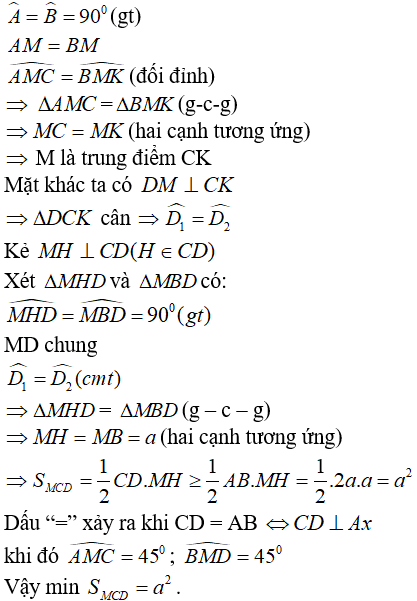
Các điểm C, D được xác định trên Ax; By sao cho AC = BC = a.

C. Bài tập tự luyện

Câu 1: Trong các hình chữ nhật có chu vi là 20cm, hình nào có diện tích lớn nhất?

Câu 2: Cho đoạn thẳng AB = 6cm. Lấy điểm M bất kỳ thuộc đoạn thẳng AB. Vẽ hình vuông AMND và BMPQ về cùng một phía đối với đường thẳng AB. Tìm giá trị nhỏ nhất của tổng diện tích hai hình vuông đó?

Câu 3: Cho tam giác ABC vuông cân tại A và BC = 36cm. Vẽ hình vuông MNPQ sao cho 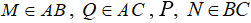. Xác định vị trí của N và P để diện tích hình chữ nhật MNPQ lớn nhất.

Câu 4: Cho M, N, P lần lượt thuộc cạnh AB, BC, CA của tam giác ABC sao cho 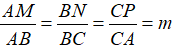. Xác định vị trí của M, N, P để diện tích tam giác MNP nhỏ nhất.

Câu 5: Cho ΔABC vuông cân tại A và cạnh BC = a. Gọi M là trung điểm của BC. Các điểm D, E thay đổi theo thứ tự nằm trên cạnh AB, AC sao cho BD = AE. Tìm giá trị nhỏ nhất của diện tích ΔMDE.