Phương pháp Phân tích đa thức thành nhân tử
Phương pháp Phân tích đa thức thành nhân tử
Tài liệu Phương pháp Phân tích đa thức thành nhân tử Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
A. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung:
I. Lý thuyết
- Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.
- Phương pháp đặt nhân tử chung là một phương pháp để phân tích đa thức thành nhân tử bằng cách nhóm các hạng tử có chung nhân tử:
A.B + A.C = A.(B + C)
II. Các dạng bài:
1. Dạng 1: Phân tích đa thức thành nhân tử:
a. Phương pháp giải:
Phân tích các hạng tử của đa thức để chọn nhân tử chung thích hợp, sau đó áp dụng tính chất phân phối của phép nhân với phép cộng
b, Ví dụ minh họa:
Phân tích các đa thức sau thành nhân tử:
a, x2 - 3x
= x.x – 3x
= x.(x – 3)
b, 3x – 6y
= 3x – 2.3.y
= 3.(x – 2y)
c, x(y - x)2 + xy(x - y)
= x(x - y)2 + xy(x - y)
= x.(x – y)(x – y) + xy(x – y)
= x.(x – y).[(x – y) + y]
= x2(x – y)
2. Dạng 2: Các bài toán liên quan
a. Phương pháp giải:
Phân tích các hạng tử của đa thức để chọn nhân tử chung thích hợp, sau đó áp dụng tính chất phân phối của phép nhân với phép cộng để làm một số bài toán tính nhanh, tính giá trị biểu thức, tìm x,…
b. Ví dụ minh họa
VD1: Tính nhanh:
a, 75.20,9 + 52.20,9
= 20,9.(75 + 52)
= 20,9.100
= 2090
b, 98,6.199 – 990.9,86
= 98,6.199 – 99.10.9,86
= 98,6.199 – 98,6.99
= 98,6.(199 – 99)
= 98,6.100
= 9860
VD2: Tính giá trị biểu thức:
a, A = a(b + 3) – b(3 + b) tại a = 2, b = 3
A = a(b + 3) – b(b + 3)
= (b + 3)(a – b)
Thay a = 2, b = 3 vào biểu thức A ta được:
A = (3 + 3)(2 – 3) = - 6
b, B = b2 - 8b – c(8 – b) tại b = 1, c = 2
Ta có:
B = b2 - 8b – c(8 – b)
= -b(8 – b) – c(8 – b)
= (8 – b)(- b – c)
Thay b = 1, c = 2 vào biểu thức B, ta được:
B = (8 – 1)(- 1 – 2)
= -21
VD3: Tìm x, biết:
a, 8x(x – 2017) – 2x + 4034 = 0
⇔ 8x(x – 2017) – 2(x - 2017) = 0
⇔ (x – 2017)(8x - 2x) = 0
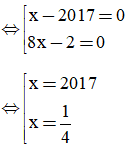
Vậy x = 2017 , x =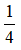 
b, 4 – x = 2(x – 4)2
⇔ 2(x – 4)2 + x - 4 = 0
⇔ (x – 4)[2(x – 4) + 1] = 0
⇔ (x – 4)(2x – 8 + 1) = 0
⇔ (x – 4)(2x – 7) = 0
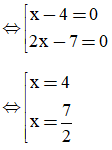
Vậy = 4, x =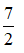 
3. Dạng 3: Chứng minh các bài toán số nguyên:
a. Phương pháp giải:
Phân tích các biểu thức đã cho một cách hợp lí thành các tích và sử dụng tính chất chia hết của số nguyên.
b. Ví dụ minh họa:
Chứng minh:
a, 25n+1 - 25n chia hết cho 100 với mọi số tự nhiên n ≠ 0
Ta có:
25n+1 - 25n
= 25n (25 – 1)
= 24.25n
Ta lại có: 24 = 4.6
25n = 25.25n-1
=> 25n+1 - 25n = 4.6.25.25n-1
= 100.6.25n-1 ⋮ 100 với mọi n ∈ N∗
Vậy 25n+1 - 25n chia hết cho 100 với mọi số tự nhiên n ≠ 0
b, n2(n - 1) - 2n(n - 1) chia hết cho 6 với mọi số nguyên n
Ta có:
n2(n - 1) - 2n(n - 1)
= (n – 1)(n2 - 2n)
= (n – 1).n.(n – 2)
= (n – 2).(n – 1).n
Ta có: n – 2, n – 1, n là 3 số tự nhiên liên tiếp nên tích của chúng sẽ chia hết 6
=> n2(n - 1) - 2n(n - 1) chia hết cho 6 với mọi số nguyên n.
c, 50n+2 - 50n+1 chia hết cho 245 với mọi số tự nhiên n.
Ta có:
50n+2 - 50n+1
= 50n(502 - 50)
= 50n(2500 – 50)
= 2450.50n
= 245.10.50n ⋮ 245 với mọi STN n
Vậy 50n+2 - 50n+1 chia hết cho 245 với mọi số tự nhiên n.
B. Phân tích đa thức nhân tử bằng phương pháp dùng hằng đẳng thức
I. Lý thuyết:
- Ta có thể sử dụng các hằng đẳng thức đáng nhớ theo chiều biến đổi từ một vế là một đa thức sang vế kia là một tích của các nhân tử hoặc lũy thừa của một đơn thức đơn giản hơn
1. Bình phương của một tổng: A2 + 2AB + B2 = (A + B)2
2. Bình phương của một hiệu: A2 - 2AB + B2 = (A - B)2
3. Hiệu của hai bình phương: A2 - B2 = (A + B)(A - B)
4. Lập phương của một tổng: A3 + 3A2B + 3AB2 + B3 = (A + B)3
5. Lập phương của một hiệu: A3 - 3A2B + 3AB2 - B3 = (A - B)3
6. Tổng của hai lập phương: A3 + B3 = (A + B)(A2 - AB + B2)
7. Hiệu của hai lập phương: A3 - B3 = (A - B)(A2 + AB + B2)
II. Các dạng bài:
1. Dạng 1: Phân tích đa thức thành nhân tử
a. Phương pháp giải:
Chuyển các đa thức đã cho về đúng dạng của hẳng đẳng thức cần sử dụng và phân tích thành nhân tử.
b. Ví dụ minh họa:
Phân tích đa thức thành nhân tử:
a, -4x2 + 4x - 1
= -(4x2 - 4x + 1)
= - [(2x)2 -2.2x.1 +1]
= - (2x – 1)2
= - (2x – 1)(2x – 1)
= (2x – 1)(1 – 2x)
b, 8x3 - 12x2 + 6x - 1
= (2x)3 - 3.(2x)2.1 + 3.2x.13 - 1
= (2x – 1)3
c, x2 - 5x + 6
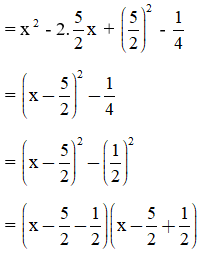
= (x – 3)(x – 2)
2. Dạng 2: Các bài toán liên quan
a. Phương pháp giải
Sử dụng hằng đẳng thức một cách hợp lý để phân tích các biểu thức để làm một số bài toán tính nhanh, tìm x,…
b. Ví dụ minh họa:
VD1: Tính nhanh:
a, 852 - 152 + 562 - 442
= (85 – 15)(85 + 15) + (56 – 44)(56 +44)
= 70.100 + 12.100
= 7000 + 1200
= 8200
b, 1033 - 9.1033 + 27.103 - 27
= 1033 - 3.1033.3+ 3.103.32 - 32
= (103 – 3)3
= 1003
= 1000000
VD2: Tìm x:
a, (x - 5)2 = (3 + 2x)2
⇔ (x - 5)2 - (3 + 2x)2 = 0
⇔ (x – 5 + 3 + 2x)(x – 5 – 3 – 2x) = 0
⇔ (3x – 2)(- x – 8) = 0
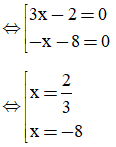
Vậy x =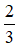 
, x = -8
b, 27x3 - 54x2 + 36x = 9
⇔ 27x3 - 54x2 + 36x - 9 = 0
⇔ (3x)2 - 3.(3x)2.2 + 3.3x.22 - 8 - 1 = 0
⇔ (3x – 2)3 - 1 = 0
⇔ (3x – 2)3 = 1
⇔ 3x – 2 = 1
⇔ x = 1
Vậy x = 1
3. Dạng 3: Chứng minh các bài toán số học:
a. Phương pháp giải:
Số nguyên a chia hết cho số nguyên b nếu có số nguyên k sao cho a = b.k. Từ đó cần phân tích biểu thức ra thừa số để xuất hiện số chia.
b. Ví dụ minh họa:
Chứng minh:
a, (3n – 1)2 - 4 chia hết cho 3 với mọi số tự nhiên n
Ta có:
(3n – 1)2 - 4 = (3n – 1)2 - 22
= (3n – 1 – 2)(3n – 1 + 2)
= (3n – 3)(3n + 1)
= 3.(n – 1)(3n +1) ⋮ 3 với mọi STN n
b, 100 - (7n + 3)2 chia hết cho 7 với mọi STN n
Ta có:
100 - (7n + 3)2 = 102 - (7n + 3)2
= (10 – 7n - 3)(10 + 7n + 3)
= (7 – 7n)(13 + 7n)
= 7.(1 – n)(13 + 7n) ⋮ 7 với mọi STN n
C. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử.
I. Lý thuyết
- Khi sử dụng phương pháp nhóm hạng tử để phân tích đa thức thành nhân tử, ta cần nhận xét đặc điểm của các hạng tử, nhóm các hạng tử một cách thích hợp nhằm làm xuất hiện dạng hằng đẳng thức hoặc xuất hiện nhân tử chung của các nhóm.
II. Các dạng bài:
1. Dạng 1: Phân tích đa thức thành nhân tử:
a. Phương pháp giải:
Nhóm các hạng tử một cách hợp lí để xuất hiện nhân tử chung hoặc xuất hiện các hằng đẳng thức
b. Ví dụ minh họa:
Phân tích các đa thức sau thành nhân tử:
a, a4 - 9a3 + a2 - 9a
= a3(a – 9) + a(a – 9)
= (a – 9)(a3 + a)
= a.(a – 9)(a2 + 1)
b, 3x2 + 5y - 3xy + (-5x)
= (3x2 - 3xy) + (5y - 5x)
= 3x(x – y) – 5( x – y)
= (x – y)(3x - 5)
c, x2 - (a + b)x + ab
= x2 - ax - bx + ab
= (x2 - ax) + (ab - bx)
= x(a – x) + b(a – x)
= (a – x)(x + b)
2. Dạng 2: Các bài toán liên quan:
a. Phương pháp giải:
Nhóm các hạng tử một cách hợp lí để xuất hiện nhân tử chung hoặc xuất hiện các hằng đẳng thức sau đó áp dụng để tính nhanh, tính giá trị biểu thức hoặc tìm x,….
b. Ví dụ minh họa:
VD1: Tính nhanh:
a. 15.64 + 25.100 + 36.15 + 60.100
= (15.64 + 36.15) + (25.100 + 60.100)
= 15.(64 + 36) + 100.(25 + 60)
= 15.100 + 100.85
= 100.(85 + 15)
= 100.100
= 10000
b, 472 + 482 - 25 + 94.48
= 472 + 482 + 2.47.48 - 25
= (47 + 48)2 - 25
= 952 - 52
= (95 – 5)(95 + 5)
= 90.100
= 9000
VD2: Tìm x:
a, x2(x - 5) + 5 - x = 0
⇔ x2(x - 5) - (x - 5) = 0
⇔ (x - 5)(x2 - 1) = 0
⇔ (x – 1)(x + 1)(x – 5) = 0
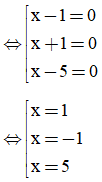
Vậy x = 1, x = -1, x = 5
b, (x + 3)(x2 - 3x + 5) = x2 + 3x
⇔ (x + 3)(x2 - 3x + 5) - (x2 + 3x) = 0
⇔ (x + 3)(x2 - 3x + 5) - x(x + 3) = 0
⇔ (x + 3)(x2 - 3x + 5 - x) = 0
⇔ (x + 3)(x2 - 4x + 5) = 0
⇔ (x + 3)(x2 - 2.2x + 22 + 1) = 0
⇔ (x + 3)[(x - 2)2 + 1] = 0
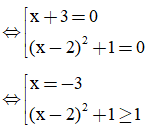
Vậy x = - 3
3. Dạng 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức dạng
ax2 + bx + c
a. Phương pháp giải:
Tách hạng tử c thành tổng c1 + c2 sao cho ax2 + bx + c1 tạo thành bình phương của một tổng hoặc bình phương của một hiệu rồi đánh giá.
b. Ví dụ minh họa:
VD1: Tìm GTNN của biểu thức:
a, A = x2 + 2x + 5
Ta có:
A = x2 + 2x + 5
= x2 + 2x + 1 + 4
= (x2 + 2x + 1) + 4
= (x + 1)2 + 4
Ta có:
(x + 1)2 ≥ 0 với mọi x
=> (x + 1)2 + 4 ≥ 4 với mọi x
=> Amin = 4 khi x +1 = 0 ⇔ x = -1
b, B = x2 - 5x + 8
Ta có:
B = x2 - 5x + 8
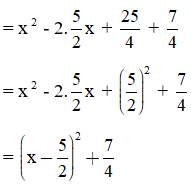
Ta có:
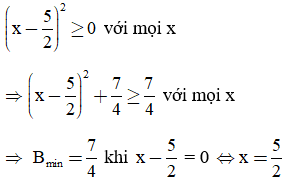
D. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp.
I. Lý thuyết:
- Một số phương pháp phân tích đa thức thành nhân tử cơ bản đã học trong các bài trước:
+ Phương pháp nhân tử chung
+ Phương pháp hằng đẳng thức
+ Phương pháp nhóm hạng tử
- Trong một số bài toán thì chúng ta cần kết hợp linh hoạt cả ba phương pháp cơ bản trên để phân tích đa thức thành nhân tử
- Ngoài ra, để phân tích đa thức thành nhân tử người ta còn sử dụng một số phương pháp khác như:
+ Phương pháp tách hạng tử
+ Phương pháp thêm, bớt cùng một hạng tử
+ Phương pháp đặt biến phụ
+ Phương pháp hệ số bất định.
…
II. Các dạng bài:
1. Dạng 1: Phân tích đa thức thành nhân tử bằng cách phối hợp các phương pháp cơ bản
a. Phương pháp giải:
Sử dụng phối hợp nhiều phương pháp cơ bản để phân tích đa thức thành nhân tử:
+ Phương pháp nhân tử chung
+ Phương pháp hằng đẳng thức
+ Phương pháp nhóm hạng tử
b. Ví dụ minh họa:
Phân tích các đa thức sau thành nhân tử:
a, 3x - 3y + x2 - y2
= 3.(x – y) + (x2 - y2)
= 3.(x – y) + (x – y)(x + y)
= (x – y)(3 + x + y)
b, x3 - 3x2 +3x - 1 - y3
= (x3 - 3x2 +3x - 1) - y3
= (x - 1)3 - y3
= (x – 1 – y)[(x - 1)2 + (x - 1)y + y2]
= (x – y – 1)(x2 - 2x + 1 + xy - y + y2)
c, x3 + x2 - x - 1
= x2(x + 1) - (x + 1)
= (x + 1)(x2 - 1)
= (x + 1)(x – 1)(x + 1)
= (x + 1)2(x – 1)
2. Dạng 2: Phân tích đa thức thành nhân tử bằng phương pháp tách hạng tử
a. Phương pháp giải:
Tách một hạng tử thành nhiều hạng tử sau đó sử dụng phương pháp nhóm hạng tử để phân tích.
Chú ý: Đối với các đa thức có dạng ax2 + bx + c (a ≠ 0) ta thường sử dụng cách tách sau để phân tích đa thức thành nhân tử:
+ Cách 1: Tách bx = b1x + b2x sao cho b1b2 = ac
+ Cách 2: Tách c = c1 + c2 sao cho ax2 + bx + c1 = (....±...)2
b. Ví dụ minh họa:
Phân tích các đa thức sau thành nhân tử:
a. x2 - 5x + 6
= x2 - 2x - 3x + 6
= (x2 - 2x) - (3x - 6)
= x(x – 2) – 3(x – 2)
= (x – 2)(x – 3)
b, 3x2 + 9x - 30
= 3x2 + 15x - 6x - 30
= (3x2 + 15x) - (6x + 30)
= 3x(x + 5) – 6(x + 5)
= (x + 5)(3x – 6)
= 3.(x + 5)(x – 2)
c, 2x2 + 5x + 2
= 2x2 + 4x + x + 2
= 2x(x + 2) + (x + 2)
= (x + 2)(2x + 1)
3. Dạng 3: Phân tích đa thức thành nhân tử bằng phương pháp đặt biến phụ
a. Phương pháp giải:
Đặt các hạng tử giống nhau thành biến mới để đưa các đa thức đã cho ở đề bài về một đa thức mới với biến vừa đặt sau đó sử dụng các phương pháp phân tích đã học ở trên để phân tích đa thức thành nhân tử.
b. Ví dụ minh họa:
Phân tích các đa thức sau thành nhân tử:
a, x4 + 3x2 - 4
Đặt x2 = t, ta được:
t2 + 3t - 4 = t2 + 4t - t - 4
= (t2 + 4t) - (t + 4)
= t.(t + 4) – (t + 4)
= (t + 4)(t – 1)
Thay x2 = t vào ta được:
x4 + 3x2 - 4 = (x2 + 4)(x2 - 1)
= (x2 + 4)(x - 1)(x + 1)
b, (x - 1)4 - 2(x2 - 2x + 1)2 + 1
= (x - 1)4 - 2[(x - 1)2]2 + 1
Đặt t = (x - 1)2, ta được:
t2 - 2t2 + 1
= 1 – t2
= (1 – t)(1 + t)
Thay t = (x - 1)2 ta có:
(x - 1)4 - 2(x2 - 2x + 1)2 + 1
= [1 - (x - 1)2][1 + (x - 1)2]
= (1 - x2 + 2x - 1)(1 + x2 - 2x + 1)
= (-x2 + 2x)(x2 - 2x + 2)
= x(2 – x)(x2 - 2x + 2)
c, (x + 1)(x + 2)(x + 3)(x + 4) – 24
Ta có:
(x + 1)(x + 2)(x + 3)(x + 4) – 24
= [(x + 1)(x + 4)][(x + 2)(x + 3)] – 24
= (x2 + 5x + 4)(x2 + 5x + 6) – 24
Đặt t = x2 + 5x ta được:
(t + 4)(t + 6) – 24
= t2 + 10t + 24 - 24
= t2 + 10t
= t(t + 10)
Thay t = x2 + 5x, ta có:
(x + 1)(x + 2)(x + 3)(x + 4) – 24
= (x2 + 5x)(x2 + 5x +10)
E. Bài tập tự luyện.
Bài 1: Phân tích các đa thức sau thành nhân tử
a, 4x2 - 6x
b, 9x4y3 + 3x2y4
c, 3(x - y) - 5x(y - x)
d, 5(x + 3y) – 15x(x + 3y)
Hướng dẫn giải:
a, 2x(2x – 3)
b, 3x2y3(3x2 + y)
c, (x – y)(3 + 5x)
d, 5(x + 3y)(1 – 3x)
Bài 2: Phân tích đa thức thành nhân tử
a, 4(2 - x)2 + xy - 2y
b, 3a2x - 3a2y + abx - aby
c, x(x - y)3 - y(y - x)2 - y2(x - y)
d, 2ax3 + 6ax2 + 6ax + 18a
Hướng dẫn giải:
a, (x – 2)(8x +y – 8)
b, a(x – y)(3a + b)
c, (x – y)[x(x - y)2 - xy]
d, 2a.(x + 3)(x2 + 3)
Bài 3: Tính hợp lí
a, 86.15 + 150.1,4
b, 93.32 + 14.16
c, -8.40 + 2.108 + 24
d, 993.98 + 21.331 - 50.99,3
Hướng dẫn giải:
a, 1500
b, 3200
c, -80
d, 99300
Bài 4: Tính giá trị biểu thức
a, A = a(b + 3) - b(3 + b) tại a = 2003 và b = 1997
b, B = b2 - 8b - c(8 - b) tại b = 108 và c = -8
c, C = xy(x + y) - 2x - 2y tại xy = 8 và x + y = 7
d, x5(x + 2y) - x3y(x + 2y) + x2y2(x + 2y) tại x = 10 và y = -5
Hướng dẫn giải:
a) A = a(b + 3) - b(3 + b) = (b + 3)(a - b)
Tại a = 2003 và b = 1997, ta có
A = (1997 + 3)(2003 - 1997) = 2000.6 = 12000
b) B = b2 - 8b - c(8 - b) = b(b - 8) + c(b - 8) = (b - 8)(b + c)
Tại b = 108 và c = -8, ta có B = (108 - 8)(108 - 8) = 100.100 = 10000
c) C = xy(x + y) - 2x - 2y = (x + y)(xy - 2)
Tại xy = 8 và x + y = 7, ta có C = 7.(8 - 2) = 7.6 = 42.
d) x5(x + 2y) - x3y(x + 2y) + x2y2(x + 2y) = x2(x + 2y)(x3 - xy + y2)
Tại x = 10 và y = -5, ta có x + 2y = 10 + 2.(-5) = 0 suy ra D = 0
Bài 5: Tìm x , biết
a, x(x + 2018) + 2x + 4036 = 0
b,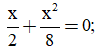 
c, (x2 + 1)(x - 2) + 2x = 4
d, x + 5 = 2(x + 5)2
Hướng dẫn giải:
a, x = -2018, x = - 2
b, x = 0, x = -4
c, x = 2
d, x = -5, x =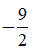 
Bài 6:
a) 15n + 15n+2 chia hết cho 113 với mọi số tự nhiên n
b) n4 - n2 chia hết cho 4 với mọi số tự nhiên n
Hướng dẫn giải:
a) 15n + 15n+2
= 15n (1 + 152)
= 15n.226
= 15n.2.113 ⋮ 113 với mọi số tự nhiên n
b) n4 - n2 = n2(n2 - 1)
= n2(n - 1)(n + 1)
= (n - 1)n.n(n + 1) ⋮ 4 với mọi số tự nhiên n
Bài 7: Phân tích các đa thức sau thành nhân tử:
a, 4x2 - 12x + 9
b, 4x2 + 4x + 1
c, 1 + 12x + 36x2
d, 9x2 - 24xy + 16y2
Hướng dẫn giải:
a, (2x – 3)2
b, (2x + 1)2
c, (1 + 6x)2
d, (3x – 4y)2
Bài 8: Phân tích các đa thức sau thành nhân tử:
a, (3x – 1)2 - 16
b, (5x – 4)2 - 49x2
c, (2x + 5)2 - (x – 9)2
d, (3x + 1)2 - 4(x – 2)2
Hướng dẫn giải:
a) 3(3x – 1)(x + 1)
b) -8(x + 2)(3x – 1)
c) (x + 14)(3x – 4)
d) (x + 5)(5x – 3)
Bài 9: Phân tích các đa thức sau thành nhân tử:
a, 8x3 - 64
b, 1 + 8x6y3
c, 27x3 +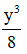 
d, 125x3 + 27y3
Hướng dẫn giải:
a, 8.(x – 2)(x2 + 2x + 4)
b, (1 + 2x2y)(1 - 2x2y + 4x4y2)
c,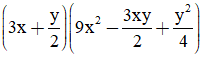 
d, (5x + 3y)(25x2 - 15xy +9y2)
Bài 10: Phân tích các đa thức sau thành nhân tử:
a, x3 + 6x2 + 12x + 8
b, x3 - 3x2 + 3x - 1
c, 1 - 9x + 27x2 - 27x3
d,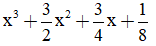 
e, 27x3 - 54x2y + 36xy2 - 8y3
Hướng dẫn giải:
a, x3 + 6x2 + 12x + 8 = (x + 2)3
b, x3 - 3x2 + 3x - 1 = (x - 1)3
c, 1 - 9x + 27x2 - 27x3 = (1 - 3x)3
d,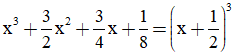 
e, 27x3 - 54x2y + 36xy2 - 8y3 = (3x - 2y)3
Bài 11: Phân tích các đa thức sau thành nhân tử:
a, (xy + 1)2 - (x + y)2
b, (x + y)3 - (x - y)3
c, 3x4y2 + 3x3y2 + 3xy2 + 3y2
Hướng dẫn giải:
a, (xy + 1)2 - (x + y)2
= (xy + 1 - x - y)(xy + 1 + x + y)
= [x(y - 1) - (y - 1)][x(y + 1) + (y + 1)]
= (x - 1)(y - 1)(x + 1)(y + 1)
b, (x + y)3 - (x - y)3
= (x + y - x + y)[(x + y)2 + (x + y)(x - y) + (x - y)2]
= 2y(x2 + 2xy + y2 + x2 - y2 + x2 - 2xy + y2)
= 2y(3x2 + y2)
c, 3x4y2 + 3x3y2 + 3xy2 + 3y2
= 3y2(x4 + x3 + x + 1)
= 3y2[x3(x + 1) + (x + 1)]
= 3y2(x + 1)(x3 + 1)
= 3y2(x + 1)2(x2 - x + 1)
Bài 12: Phân tích các đa thức sau thành nhân tử
a, x2 + 2x - 8
b, x2 + 5x + 6
c, 4x2 - 12x + 8
d, 3x2 + 8xy + 5y2
Hướng dẫn giải:
a, x2 + 2x - 8
= (x + 1)2 - 9
= (x - 2)(x + 4)
b, x2 + 5x + 6
= x2 + 4x + 4 + x + 2 .
= (x + 2)2 + (x + 2)
= (x + 2)(x + 3)
c, 4x2 - 12x + 8 .
= 4x2 - 12x + 9 - 1
= (2x - 3)2 - 12
= 4(x - 2)(x - 1)
d, 3x2 + 8xy + 5y2 .
= 3(x2 + 2xy + y2) + 2xy + 2y2
= 3(x + y)2 + 2y(x + y)
= (x + y)(3x + 5y)
Bài 13: Tìm x , biết
a, (2x - 5)2 - (5 + 2x)2 = 0
b, 27x3 - 54x2 + 36x = 8
c, (x3 + 8) - (x + 2)(x - 4) = 0
d, x6 - 1 = 0
Hướng dẫn giải:
a, x = 0 .
b, x =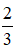 
c, x = -2
d, x = ± 1
Bài 14: Chứng minh
a, 29 - 1 chia hết cho 73
b, 56 - 104 chia hết cho 9
c, (n + 3)2 - (n - 1)2 chia hết cho 8 với mọi số tự nhiên n
d, (n + 6)2 - (n - 6)2 chia hết cho 24 với mọi số tự nhiên
Hướng dẫn giải:
a, 29 - 1.
= (23 - 1)(26 + 23 + 1)
= 7.73 ⋮ 73
b, 56 - 104 .
= (53)2 - 12 + 12 - (102)2
= (53 - 1)(53 + 1) + (1 - 102)(1 + 102)
= (124.126 - 99.101) ⋮ 9
=> (124.126 - 99.101) ⋮ 9
c, (n + 3)2 - (n - 1)2.
= (n + 3 - n + 1)(n + 3 + n - 1)
= 8.(n + 1) ⋮ 8
d, (n + 6)2 - (n - 6)2.
= (n + 6 - n + 6)(n + 6 + n - 6)
= 24n ⋮ 24
Bài 15: Tính nhanh
a, 852 - 152
b, 932 + 21.932 + 3.49.93 + 343
c, 732 - 132 - 102 + 20.13
d,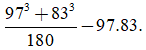 
Hướng dẫn giải:
a, 7000.
b, 1000000
c, 5320.
d, 196
Bài 16: Phân tích các đa thức sau thành nhân tử:
a, 2x2 - 2xy - 3x + 3y
b, -x2 - y2 + 2xy + 16
c, y2 - x2 + 2yz + z2
d, 3x2 - 6xy + 3y2 - 12z2
Hướng dẫn giải:
a, (x - y)(2x - 3)
b, (4 - x + y)(4 + x - y)
c, (y + z - x)(y + z + x)
d, 3(x - y + 2z)(x - y - 2z)
Bài 17: Phân tích các đa thức sau thành nhân tử:
a, x4 - 2x3 + 2x - 1
b, a6 - a4 + 2a3 + 2a2
c, x4 + x3 + 2x2 + x + 1
d, x4 + 2x3 + 2x2 + 2x + 1
e, x2y + xy2 + x2z + y2z + 2xyz
f, x5 + x4 + x3 + x2 + 1
Hướng dẫn giải:
a, x4 - 2x3 + 2x - 1
= (x4 - 1) - (2x3 - 2x)
= (x2 - 1)(x2 + 1) - 2x(x2 - 1)
= (x2 - 1)(x2 + 1 - 2x)
= (x - 1)(x + 1)(x - 1)2
= (x + 1)(x - 1)3
b, a6 - a4 + 2a3 + 2a2
= a4(a - 1)(a + 1) + 2a2(a + 1)
= a2(a + 1)(a3 - a2 + 2)
= a2(a + 1)(a3 + a2 - 2a2 + 2)
= a2(a + 1)[a2(a + 1) - 2(a + 1)(a - 1)]
= a2(a + 1)2(a2 - 2a + 2)
c, x4 + x3 + 2x2 + x + 1
= (x4 + 2x2 + 1) + (x3 + x)
= (x2 + 1)2 + x(x2 + 1)
= (x2 + 1)(x2 + x + 1)
d, x4 + 2x3 + 2x2 + 2x + 1
= (x4 + 2x2 + 1) + (2x3 + 2x)
= (x2 + 1)2 + 2x(x2 + 1)
= (x2 + 1)(x2 + 2x + 1)
= (x2 + 1)(x + 1)2
e, (x + y)(xy + yz + zx)
f, (x + 1)(x4 + x2 + 1)
Bài 18: Phân tích đa thức thành nhân tử rồi tính giá trị của biểu thức:
a) A = xy - 4y - 5x + 20, với x = 14; y = 5,5 ;
b) B = x2 + xy - 5x - 5y; với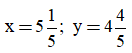 
c) C = xyz - (xy + yz + zx) + x + y + z - 1, với x = 9; y = 10; z = 11
d) D = x3 - x2y - xy2 + y3 với x = 5,75; y = 4,25
Hướng dẫn giải:
a, A = 5
b, B = 2
c, C = 720
d, D = 22,5
Bài 19: Tính nhanh
a, 93 - 92.(-1) - 9.11 + (-1).11
b, 2016.2018 - 20172
Hướng dẫn giải:
a, 700
b, - 1
Bài 20: Tìm x biết
a, 3x4 - 9x3 = -9x2 + 27x
b, x2(x + 8) + x2 = -8x
Hướng dẫn giải:
a, x = 0, x = 3
b, x = -8, x = -1, x = 0
Bài 21: Phân tích các đa thức sau thành nhân tử: (tách một hạng tử thành nhiều hạng tử)
a, 3x2 - 5x - 2
b, 2x2 + x - 6
c, 7x2 + 50x + 7
d, 12x2 + 7x - 12
Hướng dẫn giải:
a, (3x + 1)(x – 2)
b, (x + 2)(2x – 3)
c, (x + 7)(7x + 1)
d, (3x + 4)(4x – 3)
Bài 22: Phân tích các đa thức sau thành nhân tử: (tách một hạng tử thành nhiều hạng tử)
a, x2 + 4xy - 21y2
b, 5x2 + 6xy + y2
c, x2 + 2xy - 15y2
d, (x - y)2 + 4(x - y) - 12
Hướng dẫn giải:
a, (x + 7y)(x - 3y)
b, (x + y)(5x + y)
c, (x – 3y)(x + 5y)
d, (x – y – 2)(x – y + 6)
Bài 23: Phân tích các đa thức sau thành nhân tử: (tách một hạng tử thành nhiều hạng tử)
a, a4 + a2 + 1
b, a4 + a2 - 2
c, x4 + 4x2 - 5
d, x3 - 19x - 30
Hướng dẫn giải:
a) a4 + a2 + 1 = a4 + 2a2 + 1 - a2
= (a2 + 1)2 - a2
= (a2 - a + 1)(a2 + a + 1)
b) a4 + a2 - 2 = a4 - 1 + a2 - 1
= (a2 - 1)(a2 + 2)
= (a - 1)(a + 1)(a2 + 2)
c) x4 + 4x2 - 5
= x4 - x2 + 5x2 - 5
= (x2 - 1)(x2 + 5)
= (x - 1)(x + 1)(x2 + 5)
d) x3 - 19x - 30
= x3 + 8 - 19x - 38
= (x + 2)(x2 - 2x + 4) - 19(x + 2)
= (x + 2)(x2 - 2x - 15)
= (x + 2)(x2 - 2x + 1 - 16)
= (x + 2)(x - 5)(x + 3)
Bài 24: Phân tích các đa thức sau thành nhân tử: (thêm bớt cùng một hạng tử)
a) x4 + 4
b) x4 + 64
c) x8 + x7 + 1
d) x8 + x4 + 1
Hướng dẫn giải:
a) x4 + 4
= x4 + 4x2 + 4 - 4x2
= (x2 + 2)2 - 4x2
= (x2 + 2 - 2x)(x2 + 2 + 2x)
b) x4 + 64
= x4 + 16x2 + 64 - 16x2
= (x2 + 8)2 - 16x2
= (x2 + 8 - 4x)(x2 + 8 + 4x)
c) x8 + x7 + 1
= x8 - x2 + x7 - x + x2 + x + 1
= (x2 + x + 1)(x6 - x4 + x3 - x + 1)
d) x8 + x4 + 1
= x8 + 2x4 + 1 - x4
= (x4 + 1)2 - x4
= (x4 - x2 + 1)(x4 + x2 + 1)
= (x4 - x2 + 1)(x4 + 2x2 + 1 - x2)
= (x4 - x2 + 1)(x2 + x + 1)(x2 - x + 1)
Bài 25: Phân tích các đa thức sau thành nhân tử: (đặt biến phụ)
a, (x2 + x)2 - 14(x2 + x) + 24
b, (x2 + x)2 - 4x2 + 4x - 12
c, x4 + 2x3 + 5x2 + 4x - 12
d, (x + 1)(x + 2)(x + 3)(x + 4) + 1
Hướng dẫn giải:
a, (x2 + x)2 - 14(x2 + x) + 24
Đặt x2 + x = t khi đó đa thức đã cho trở thành
t2 - 14t + 24
= t2 - 12t - 2t + 24
= (t - 2)(t - 12)
Thay x2 + x = t ta được
(x2 + x - 2)(x2 + x - 12)
b, (x2 + x)2 - 4x2 + 4x - 12
= (x2 + x)2 - 4(x2 + x) - 12
Đặt x2 + x = t khi đó đa thức đã cho trở thành:
t2 + 4t - 12
= t2 + 6t - 2t - 12
= (t + 6)(t - 2)
Thay x2 + x = t ta được
(x2 + x + 6)(x2 + x - 2)
= (x2 + x + 6)(x2 - 1 + x - 1)
= (x2 + x + 6)(x - 1)(x + 2)
c, x4 + 2x3 + 5x2 + 4x - 12
= x4 + 2x3 + x2 + 4x2 + 4x - 12
= (x2 + x)2 + 4(x2 + x) - 12
= (x2 + x + 6)(x - 1)(x + 2)
(Khi đó bài toán trở về bài phần b,)
d) (x + 1)(x + 2)(x + 3)(x + 4) + 1
= (x + 1)(x + 4)(x + 2)(x + 3) + 1
= (x2 + 5x + 4)(x2 + 5x + 6) + 1
Đặt x2 + 5x + 5 = t khi đó đa thức đã cho trở thành:
(t - 1)(t + 1) + 1
= t2 -1 + 1
= t2 = (x2 + 5x + 5)2
Bài 26: Phân tích các đa thức sau thành nhân tử: (đặt biến phụ)
a, (x2 + 4x + 8)2 + 3x(x2 + 4x + 8) + 2x2
b, (x2 + x + 1)(x2 + x + 2) - 12
c, (x2 + 8x + 7)(x2 + 8x + 15) + 15
d, (x + 2)(x + 3)(x + 4)(x + 5) - 24
Hướng dẫn giải:
a) Đặt x2 + 4x + 8 = t khi đó đa thức đã cho trở thành
(x2 + 4x + 8)2 + 3x(x2 + 4x + 8) + 2x2
= t2 + 3xt + 2x2
= t2 + xt + 2xt + 2x2
= t(t + x) + 2x(t + x)
= (2x + t)(t + x)
= (2x + x2 + 4x + 8)(x2 + 4x + 8 + x)
= (x2 + 6x + 8)(x2 + 5x + 8)
= (x + 2)(x + 4)(x2 + 5x + 8)
b) Đặt x2 + x + 1 = t khi đó đa thức đã cho trở thành:
t(t + 1) - 12
= t2 + t - 12
= (t + 4)(t - 3)
(x2 + x + 1)(x2 + x + 2) - 12
= (x2 + x + 5)(x2 + x - 2)
= (x2 + x + 5)(x - 1)(x + 2)
c) (x2 + 8x + 7)(x2 + 8x + 15) + 15
Đặt x2 + 8x + 11 = t khi đó đa thức đã cho trở thành
(t - 4)( t + 4) + 15
= t2 - 16 + 15
= t2 - 1
= (t - 1)(t + 1)
= (x2 + 8x + 10)(x2 + 8x + 12)
d) (x + 2)(x + 3)(x + 4)(x + 5) - 24
= (x2 + 7x + 10)(x2 + 7x + 12) - 24
Đặt x2 + 7x + 11 = t khi đó đa thức đã cho trở thành
(t - 1)(t + 1) - 24
= t2 - 25
= (t - 5)(t + 5)
= (x2 + 7x + 6)(x2 + 7x + 16)
= (x + 1)(x + 6)(x2 + 7x + 16)
Bài 27: Tìm x biết:
a, x2 - 10x + 16 = 0
b, x2 - 11x - 26 = 0
c, 2x2 + 7x - 4 = 0
Hướng dẫn giải:
a, x= 8, x = 2
b, x = -2, x =13
c, x = -4, x =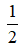 
Bài 28: Tìm x biết:
a, (x - 2)(x - 3) + (x - 2) -1 = 0
b, (x - 2)2 - 2x(2x + 3) = (x + 1)2
c, 6x3 + x2 = 2x
d, x8 - x5 + x2 - x + 1 = 0
Hướng dẫn giải:
a, x = 3, x = 1
b,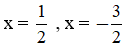 
c, x = 0,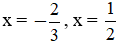 
d, Phương trình vô nghiệm
Bài 29: Chứng minh với mọi số nguyên n thì A = n4 - 2n3 - n2 + 2n chia hết cho 24.
Hướng dẫn giải:
Gợi ý: A = (n -2)(n3 - n) = (n - 2)(n - 1)n(n + 1)
A là tích của 4 số tự nguyên liên tiếp nên A chia hết cho 2 ,cho 3 và cho 4. Vì (2,3) = 1 nên A chia hết cho 6. Suy ra A chia hết cho 4.6 = 24
Bài 30: Tính (a - b)2017 biết a + b = 9, ab = 20, a < b
Gợi ý: 81 = (a + b)2 = (a - b)2 + 4ab => (a - b)2 = 1 => a - b = -1 => A = -1
( a = 4; b = 5 suy ra (a - b)2017 = -1 )
