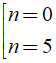Bài tập Đa giác. Đa giác đều chọn lọc, có đáp án
Bài tập Đa giác. Đa giác đều chọn lọc, có đáp án
Haylamdo biên soạn và sưu tầm Bài tập Đa giác. Đa giác đều chọn lọc, có đáp án Toán lớp 8 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm bài tập từ đó đạt điểm cao trong bài thi môn Toán lớp 8.
I. Bài tập trắc nghiệm
Bài 1: Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?
A. Hình vuông là đa giác đều.
B. Tổng các góc của đa giác lồi 8 cạnh là 10800.
C. Hình thoi là đa giác đều.
D. Số đo góc của hình bát giác đều là 135,50.
Ta cần nhớ định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
+ Hình vuông là hình có 4 cạnh bằng nhau và 4 góc bằng nhau
⇒ Hình vuông là đa giác đều.
⇒ Đáp án A đúng.
+ Hình thoi là hình có 4 cạnh bằng nhau nhưng 4 góc không bằng nhau.
⇒ Hình thoi không phải là đa giác đều.
⇒ Đáp án C sai.
+ Tổng số đo các góc của đa giác n cạnh là ( n - 2 ).1800.
Khi đó tổng các góc của đa giác lồi 8 cạnh là ( 8 - 2 ).1800 = 10800.
⇒ Đáp án B đúng.
+ Số đo của một góc của đa giác đều n cạnh là (( n - 2 ).1800)/n.
Khi đó số đo của hình bát giác đều là (( 8 - 2 ).1800)/8 = 1350.
⇒ Đáp án D sai.
Bài 2: Một đa giác 7 cạnh thì số đường chéo của đa giác đó là ?
A. 12. B. 13.
C. 14. D. Kết quả khác.
Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2.
Khi đó số đường chéo của đa giác 7 cạnh là (7( 7 - 3 ))/2 = 14 (đường chéo)
Chọn đáp án C.
Bài 3: Một đa giác có số đường chéo bằng số cạnh của đa giác thì đa giác có số cạnh là?
A. 5. B. 6.
C. 4. D. 7.
Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2. ( n ∈ N, n ≥ 3 )
Theo giả thiết ta có (n( n - 3 ))/2 = n ⇔ n( n - 3 ) = 2n ⇔ n2 - 3n - 2n = 0
⇔ n2 - 5n = 0 ⇔ n( n - 5 ) = 0 ⇔ 
So sánh điều kiện ta có n = 5 thỏa mãn.
Bài 4: Tổng số đo các góc của đa giác 12 cạnh là?
A. 1800o B.1600o
C. 1720o D. 1440o
Tổng số đo các góc của đa giác n cạnh là (n -2).180o
Do đó, Tổng số đo các góc của đa giác 12 cạnh là (12 – 2).180o = 1800o
Chọn đáp án A
Bài 5: Số đường chéo xuất phát từ 1 đỉnh của đa giác 20 cạnh là?
A. 15 B. 16
C. 17 D. 18
Số đường chéo xuất phát từ 1 đỉnh của đa giác n cạnh là n – 3
Do đó, Số đường chéo xuất phát từ 1 đỉnh của đa giác 20 cạnh là: 20 – 3 = 17
Chọn đáp án C
Bài 6: Số đường chéo của đa giác 10 cạnh?
A. 50 B. 60
C. 70 D. 80
Số đường chéo xuất phát từ 1 đỉnh của đa giác 10 cạnh là: 10 – 3 = 7
Suy ra: số đường chéo của đa giác 10 cạnh là: 7.10 = 70 đường chéo
Chọn đáp án B
Bài 7: Số đo mỗi góc của 10- giác đều là:
A. 100o B. 120o
C. 136o D. 144o
Tổng số đo các góc của 10 – giác đều là: (10 - 2). 180o = 1440o
Do đây là 10 – giác đều nên số đo các góc bằng nhau và bằng: 144o: 10 = 144o
Chọn đáp án D
Bài 8: Cho đa giác đều n cạnh. Biết số đo mỗi góc bằng 140o. Tìm n?
A. n = 9 B. n = 8
C. n = 7 D. n = 10
Tổng số đo các góc của đa giác n cạnh là: 140.n
Mặt khác đa giác n cạnh thì có tổng số đo các góc của đa giác là: (n-2). 180
Suy ra: 140n = (n – 2). 180
⇔ 140n = 180n - 360
⇔ 40n = 360 ⇔ n = 9
Chọn đáp án A
Bài 9: Cho đa giác đều 11 cạnh có độ dài mỗi cạnh là 5cm. Tính chu vi đa giác
A. 45cm B. 50cm
C. 60cm D. 55cm
Chu vi của đa giác đều 11 cạnh là: 5.11 = 55 cm
Chọn đáp án D
Bài 10: Hình vuông có mấy trục đối xứng?
A. 1 B. 2
C. 3 D. 4
Hình vuông có 4 trục đối xứng bao gồm:
+ 2 đường chéo của hình vuông
+ 2 đường thẳng đi qua tâm và song song với 2 cạnh của hình vuông
Chọn đáp án D
