Vận dụng tính chất đường phân giác để chứng minh các hệ thức

Vận dụng tính chất đường phân giác để chứng minh các hệ thức

Tài liệu Vận dụng tính chất đường phân giác để chứng minh các hệ thức Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Chứng minh hệ thức hình học

A. Phương pháp giải

B. Ví dụ minh họa

Câu 1: Cho ∆ABC. Một đường thẳng song song với BC cắt các cạnh AB, AC ở D, E. Biết BD = 9cm, CE = 12cm, DE = 14cm. Điểm M nằm trên đoạn thẳng DE sao cho DM = 6cm. Chứng minh rằng AM là tia phân giác của góc A.

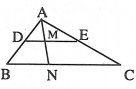Giải.

Theo giả thiết ta có:

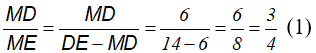
Mặt khác, do DE // BC, theo định lý Ta - let:

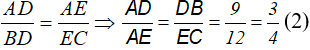
Từ (1), (2), suy ra:

Câu 2: Cho ∆ABC có các đường phân giác AD, BE, CF. Chứng minh rằng: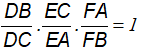

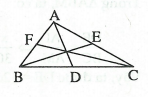
Lời giải:

Trong ∆ABC, ta lần lượt thấy:

Khi đó nhân vế với vế của (1), (2), (3) ta có:

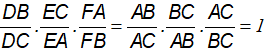
Câu 3: Cho ∆ABC với trung tuyến AM. Đường phân giác của góc AMB cắt cạnh AB ở D, đường phân giác của góc AMC cắt cạnh AC ở E. Chứng minh rằng:

a) DE // BC.

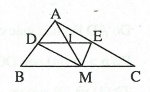b) Gọi I là giao điểm của AM và DE. Chứng minh rằng DI = IE.

c) Tính độ dài DE biết BC = 30cm, AM = 10cm.

Lời giải:

Haylamdo biên soạn và sưu tầm ∆AMB có MD là đường phân giác, suy ra:

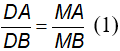
Haylamdo biên soạn và sưu tầm ∆AMC có ME là đường phân giác, suy ra:

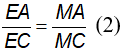
Theo giả thiết MB = MC (3)

Từ (1). (2) và (3) suy ra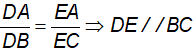

b) Xét ∆AMB có DI//BC(DE//BC)

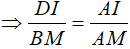( hệ quả định lý Ta- let) (4)

Xét ∆AMC có IE//MC (DE // BC)

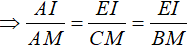( hệ quả và do AM là trung tuyến của ∆ABC nên BM = CM) (5)

Từ (4) và (5)

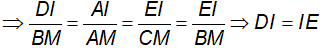
c) Đặt DE = x.

Trong ∆DEM, vì MD, ME là tia phân giác của 2 góc kề bù

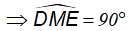
Mà DI = IE(cmt) ⇒MI là trung tuyến

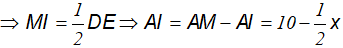
Trong ∆ABM, DE//BC hay DI//BM ta có:

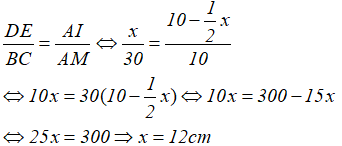
Vậy, ta được DE = 12cm.

C. Bài tập tự luyện

Câu 1: Cho tam giác ABC có trung tuyến AM. Đường phân giác góc AMC cắt AC tại H. Đường phân giác góc AMB cắt AB tại K. Chứng minh rằng HK//BC.

Câu 2: Cho tam giác ABC, kẻ tia phân giác AD. Trên tia đối của tia BA, lấy điểm F sao cho BE = BD và trên tia đối của tia CA, lấy điểm F sao cho CF = CD.

a) Chứng minh EF//BC

b) Chứng minh ED là phân giác của góc BEF và FD là phân giác của góc CFE.

Câu 3: Cho ∆ABC. Một đường thẳng song song với BC cắt các cạnh AB, AC ở D, E. Biết BD = 9cm, CE = 12cm, DE = 14cm. Điểm M nằm trên đoạn thẳng DE sao cho DM = 6cm. Chứng minh rằng AM là tia phân giác của góc A.

Câu 4: Cho ∆ABC cân tại A, có AB = a, BC = b. Đường phân giác góc B cắt AC tại M, đường phân giác góc C cắt AB tại N.

a. Chứng minh rằng MN // BC.

b. Tính độ dài đoạn MN theo a, b.

Câu 5: Đường trung tuyến BK và đường phân giác CD của ∆ABC cắt nhau tại P. Chứng minh rằng .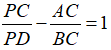

Câu 6: Cho ∆ABC cân tại A có BM, CN là các đường phân giác. Chứng minh rằng

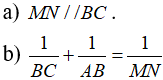
Câu 7: Cho ∆ABC cân tại A có 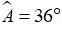. Chứng minh .

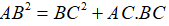Câu 8: Cho tam giác ABC vuông ở A, có góc 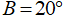; vẽ phân giác trong BI, vẽ góc 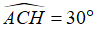về phía trong tam giác (H∈AB). Vẽ phân giác CK của góc HCB(K∈AB). Chứng minh:

.
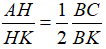