Vị trí tương đối của hai đường thẳng trong không gian

Vị trí tương đối của hai đường thẳng trong không gian

Tài liệu Vị trí tương đối của hai đường thẳng trong không gian Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Vị trí tương đối của hai đường thẳng trong không gian. Đường thẳng song song với mặt phẳng. Hai mặt phẳng song song

A. Phương pháp giải

a) Vị trí tương đối của hai đường thẳng trong không gian

+) Cắt nhau nếu có một điểm chung, chẳng hạn AB và CD.

+) Song song, nếu cùng nằm trong một nửa mặt phẳng và không có điểm chung, chẳng hạn AB//CD

+) Không cùng nằm trong một mặt phẳng nào, chẳng hạn AB và CC’

(gọi là hai đường thẳng chéo nhau).

b) Chứng minh đường thẳng song song với mặt phẳng. Hai mặt phẳng song song

+) Nếu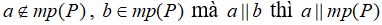

+) Để chứng minh 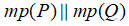ta cần chỉ ra hai đường thẳng cắt nhau của mp(P) cùng song song với mp(Q).

B. Ví dụ minh họa

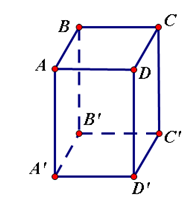
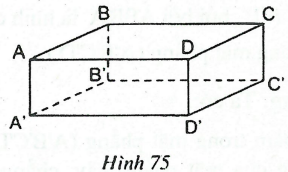
Câu 1: Quan sát hình hộp chữ nhật ở hình 75:

Hãy kể tên các mặt phẳng của hình hộp.

+) BB' và AA' có cùng nằm trong một mặt phẳng hay không?

+) BB' và AA' có điểm chung hay không?

Giải.

Ta lần lượt có:

+) Các mặt phẳng của hình hộp là:

(ABCD), (A'BC'D'), (ABB'A'), (BCC'B'), (CDD'C'), (ADD'A').

+) BB' và AA' cùng nằm trong mặt phẳng ABB'A'

+) BB' và AA' không có điểm chung, bởi là hình chữ nhật ABB'A' nên BB' và AA' song song với nhau.

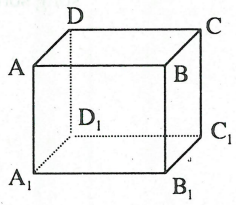
Câu 2: Cho hình hộp chữ nhật ABCD.A₁B₁C₁D₁.

a) Hãy chỉ ra các đường thẳng trong hình hộp song song với đường thẳng B₁C₁.

b) Hãy chỉ ra các mặt phẳng trong hình hộp song song với đường thẳng AB.

c) Hãy chỉ ra các đường thẳng trong hình hộp song song với mặt phẳng (A₁B₁C₁D₁).

Lời giải:

a) Ta có:

Vậy tồn tại 3 đường thẳng là BC,A₁D₁ và AD song song với B₁C₁.

b) Ta có:

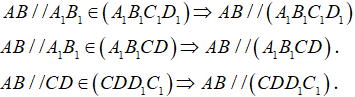
Vậy tồn tại 3 mặt phẳng (A₁B₁C₁D₁),(A₁B₁CD) và (CDD₁C₁) song song với AB.

c) Ta có:

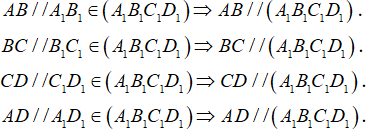
Ngoài ra, ta có:

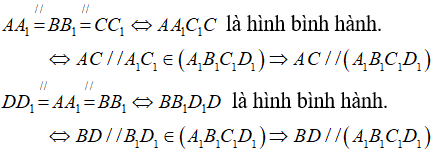
Vậy tồn tại 6 đường thẳng AB, BC, CD, AD, AC, BD song song với mặt phẳng (A₁B₁C₁D₁).

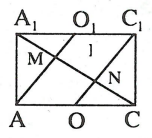
Câu 3: Cho hình lập phương ABCD.A₁B₁C₁D₁.

a) Chứng minh rằng .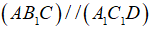

b) Gọi O là giao điểm của AC và BD. Gọi O₁ là giao điểm của A₁C₁ và B₁D₁. Các đường thẳng AO₁ và OC₁ cắt A₁C theo thứ tự tại M, N. Chứng minh rằng A₁M=MN=NC.

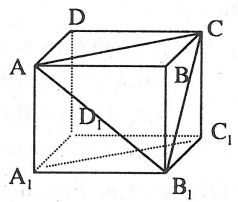
Lời giải:

a) Ta có:

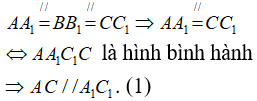
Mặt khác, ta cũng có:

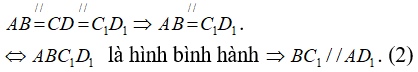
Từ (1) và (2) suy ra .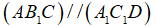

b) Ta có:

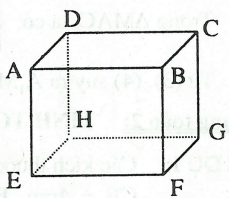
Câu 4: Cho hình hộp chữ nhật ABCD.EFGH có cạnh AB song song với mặt phẳng (EFGH).

a) Hãy liệt kê các cạnh khác song song với mặt phẳng (EFGH).

b) Cạnh CD song song với những mặt phẳng nào của hình hộp chữ nhật?

c) Chứng minh rằng AH song song với mặt phẳng (BCGF).

Lời giải:

a) Ta có:

b) Ta có:

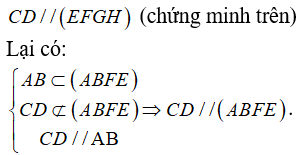
c) Ta có:

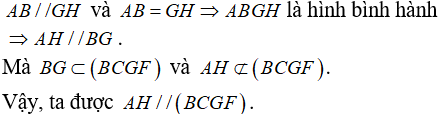
C. Bài tập tự luyện

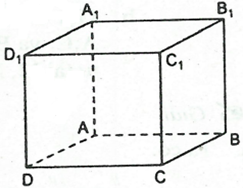
Câu 1: ABCD.A₁B₁C₁D₁ là hình lập phương.

a) Những cạnh nào song song với cạnh C₁C ?

b) Những cạnh nào song song với cạnh A₁D₁?

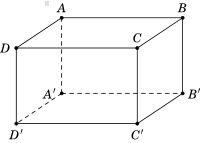
Câu 2: Cho hình hộp chũ nhật ABCD.A’B’C’D’.

a) Cạnh AB và cạnh nào cắt nhau?

b) Cạnh AB song song với cạnh nào?

c) Cạnh AB chéo nhau với cạnh nào?

Câu 3: Cho hình hộp chữ nhật ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của DD’ và CC’. Chứng minh rằng:

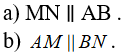
Câu 4: Cho hình hộp chữ nhật ABCD.A’B’C’D’. Gọi O là giao điểm của AC và BD; O là giao điểm của A’C’ và B’D’.

a) Điểm O có thuộc mặt phẳng (ABCD) không ? Vì sao?

b) Điểm O có thuộc đường thẳng DD’ không ? Vì sao?

c) OO’ song song với những đường thẳng nào?

Câu 5: Cho hình hộp chữ nhật ABCD.A’B’C’D’.

a) CD song song với những mặt phẳng nào?

b) AC song song với mặt phẳng nào?

Câu 6: Cho hình hộp chữ nhật ABCD.A’B’C’D’. Gọi M, N, P, Q lần lượt là trung điểm của AA’, BB’, CC’, DD’. Chứng minh rằng:

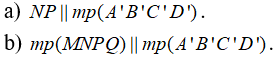
Câu 7: Cho hình hộp chữ nhật ABCD.A’B’C’D’. Gọi E, F, M, N lần lượt là trung điểm của AB, CD, A’B’ và C’D’. Chứng minh rằng 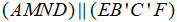.