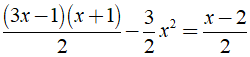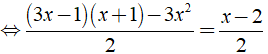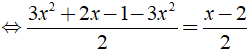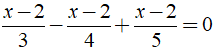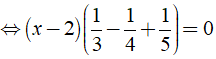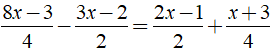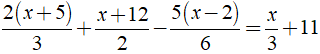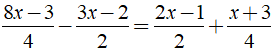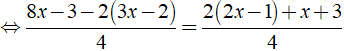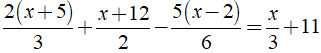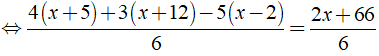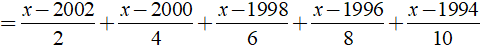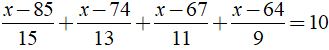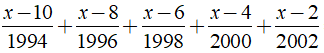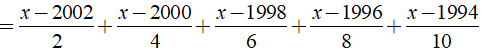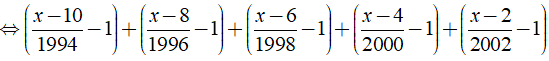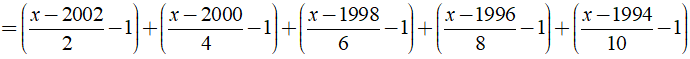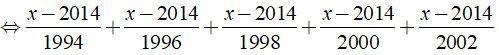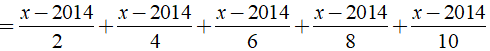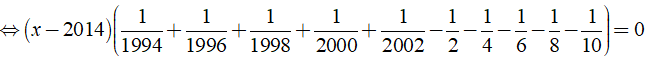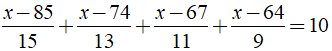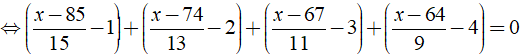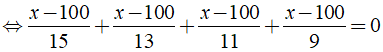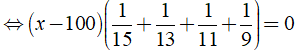Lý thuyết Phương trình đưa được về dạng ax + b = 0 hay, chi tiết

Lý thuyết Phương trình đưa được về dạng ax + b = 0 hay, chi tiết

Haylamdo biên soạn và sưu tầm Lý thuyết Phương trình đưa được về dạng ax + b = 0 hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Lý thuyết

1. Cách giải

Để giải các phương trình đưa được về ax + b = 0 ta thường biến đổi phương trình như sau:

Bước 1: Quy đồng mẫu hai vế và khử mẫu (nếu có)

Bước 2: Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng ax = c.

Bước 3: Tìm x

Chú ý: Quá trình biến đổi phương trình về dạng ax = c có thể dẫn đến trường hợp đặc biệt là hệ số của ẩn bằng 0 nếu:

0x = c thì phương trình vô nghiệm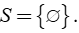

0x = 0 thì phương trình nghiệm đúng với mọi x hay vô số nghiệm S = R.

Ví dụ 1: Giải phương trình 2x - ( 3 - 2x ) = 3x + 1

Hướng dẫn:

Ta có 2x - ( 3 - 2x ) = 3x + 1 ⇔ 2x - 3 + 2x = 3x + 1

⇔ 4x - 3x = 1 + 3 ⇔ x = 4.

Vậy phương trình đã cho có tập nghiệm là S = { 4 }.

Ví dụ 2: Giải phương trình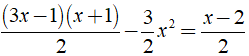

Hướng dẫn:

Ta có:

⇔ 2x - 1 = x - 2 ⇔ x = - 1.

Vậy phương trình đã cho có tập nghiệm là S = { - 1 }.

Ví dụ 3: Giải phương trình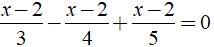

Hướng dẫn:

Ta có:

⇔ ( x - 2 )17/60 = 0 ⇔ x - 2 = 0 ⇔ x = 2.

Vậy phương trình có tập nghiệm là S = { 2 }.

Ví dụ 4: Giải phương trình x + 1 = x - 1.

Hướng dẫn:

Ta có x + 1 = x - 1 ⇔ x - x = - 1 - 1 ⇔ 0x = - 2.

Vậy phương trình đã cho vô nghiệm.

Ví dụ 5: Giải phương trình x - 3 = x - 3.

Hướng dẫn:

Ta có: x - 3 = x - 3 ⇔ x - x = - 3 + 3 ⇔ 0x = 0.

Vậy phương trình đã cho vô số nghiệm.

B. Bài tập tự luyện

Bài 1: Giải các phương trình sau:

a) 5( x - 3 ) - 4 = 2( x - 1 ) + 7

b)

c)

Hướng dẫn:

a) Ta có: 5( x - 3 ) - 4 = 2( x - 1 ) + 7

⇔ 5x - 15 - 4 = 2x - 2 + 7

⇔ 5x - 2x = 15 + 4 - 2 + 7

⇔ 3x = 24 ⇔ x = 8

Vậy phương trình đã cho có nghiệm là x = 8.

b) Ta có:

⇔ 8x - 3 - 6x + 4 = 4x - 2 + x + 3

⇔ 2x + 1 = 5x + 1

⇔ 2x - 5x = 1 - 1

⇔ -3x = 0 ⇔ x = 0

Vậy phương trình đã cho có nghiệm là x = 0.

c) Ta có:

⇔ 4x + 20 + 3x + 36 - 5x + 10 = 2x + 66

⇔ 0x = 0

⇒ Phương trình đã cho vô số nghiệm.

Vậy phương trình đã cho vô số nghiệm.

Bài 2: Giải các phương trình sau

a)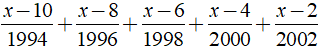

b)

Hướng dẫn:

a) Ta có:

⇒ x - 2014 = 0 ⇔ x = 2014.

Vậy phương trình đã cho có nghiệm là x = 2014.

b) Ta có:

⇒ x - 100 = 0 ⇔ x = 100.

Vậy phương trình đã cho có nghiệm là x = 100.