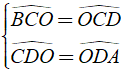Lý thuyết Tứ giác hay, chi tiết

Lý thuyết Tứ giác hay, chi tiết

Haylamdo biên soạn và sưu tầm Lý thuyết Tứ giác hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Lý thuyết

1. Định nghĩa tứ giác

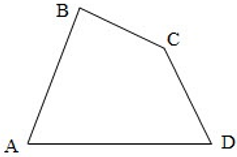
Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

Chú ý:

   Tứ giác ABCD còn được gọi tên là tứ giác BCDA,ADCB, ... . Các điểm A,B,C,D được gọi là các đỉnh. Các đoạn thẳng AB,BC,CD,DA được gọi là các cạnh.

   Tứ giác ABCD trên hình gọi là tứ giác lồi.

Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác

2. Tổng các góc của một tứ giác

Định lí: Tổng các góc của một tứ giác bằng 360⁰.

Tổng quát: Aˆ + Bˆ + Cˆ + Dˆ = 360⁰.

Ví dụ: Cho tứ giác ABCD trong đó có Aˆ = 60⁰,Cˆ = 150⁰, Dˆ = 75⁰. Tính số đo của góc Bˆ?

Hướng dẫn:

Theo định lý, tổng các góc của một tứ giác bằng 360⁰.

Khi đó ta có: Aˆ + Bˆ + Cˆ + Dˆ = 360⁰.

⇔ 60⁰ + Bˆ + 150⁰ + 75⁰ = 360⁰

⇔ Bˆ = 360⁰ - 285⁰ = 75⁰.

Vậy Bˆ = 75⁰.

B. Bài tập tự luyện

Bài 1: Cho tứ giác ABCD trong đó Aˆ = 73⁰,Bˆ = 112⁰,Dˆ = 84⁰. Tính số đo góc Cˆ?

Hướng dẫn:

Áp dụng định lí: Tổng các góc của một tứ giác bằng 360⁰.

Khi đó ta có Aˆ + Bˆ + Cˆ + Dˆ = 360⁰ ⇒ Cˆ = 360⁰ - ( Aˆ + Bˆ + Dˆ ) = 360⁰ - ( 73⁰ + 112⁰ + 84⁰ )

⇒ Cˆ = 360⁰ - 269⁰ = 91⁰.

Vậy số đo của góc Cˆ cần tìm là Cˆ = 91⁰.

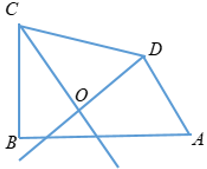
Bài 2: Cho tứ giác ABCD có Aˆ = 70⁰,Bˆ = 90⁰. Các tia phân giác của các góc C và D cắt nhau tại O. Tính số đo góc CODˆ ?

Hướng dẫn:

Áp dụng định lí: Tổng các góc của một tứ giác bằng 360⁰.

Ta có Aˆ + Bˆ + Cˆ + Dˆ = 360⁰ ⇒ Cˆ + Dˆ = 360⁰ - ( Aˆ + Bˆ ) = 360⁰ - ( 70⁰ + 90⁰ )

⇒ Cˆ + Dˆ = 200⁰

Theo giả thiết, ta có OC, OD là các đường phân giác

Khi đó ta có

⇒ Cˆ + Dˆ = BCOˆ + OCDˆ + CDOˆ + ODAˆ = 2OCDˆ + 2ODCˆ

⇔ 2( OCDˆ + ODCˆ ) = 200⁰ ⇔ OCDˆ + ODCˆ = 100⁰

Xét Δ OCD có OCDˆ + ODCˆ + CODˆ = 180⁰ ⇒ CODˆ = 180⁰ - ( OCDˆ + ODCˆ ) = 180⁰ - 100⁰ = 80⁰.

Vậy CODˆ = 80⁰.