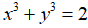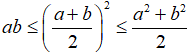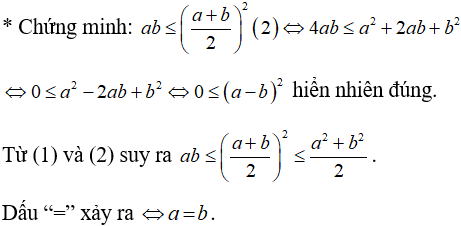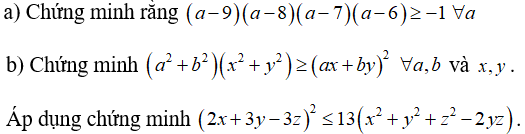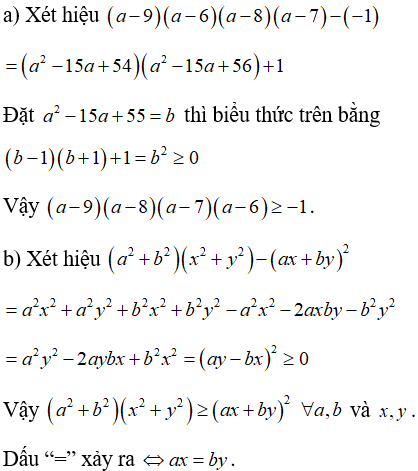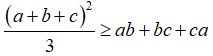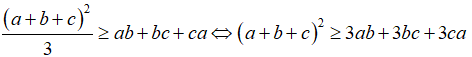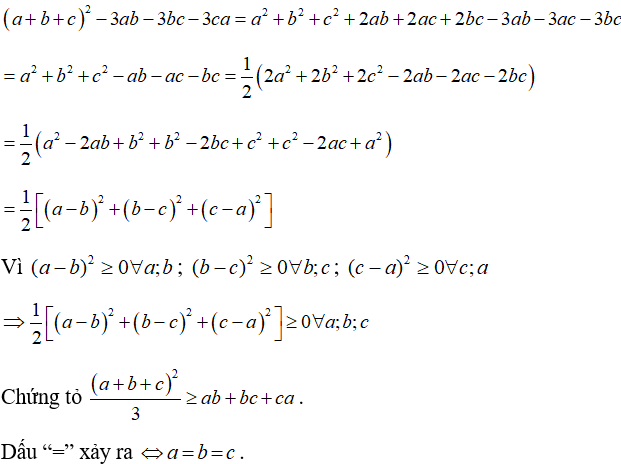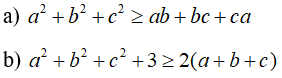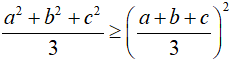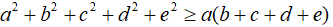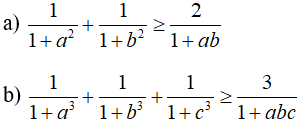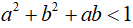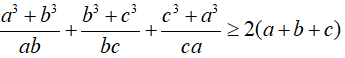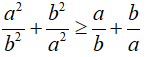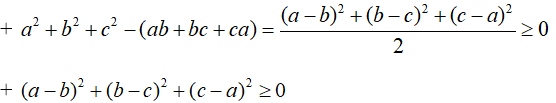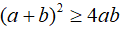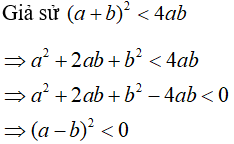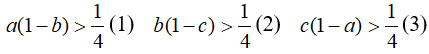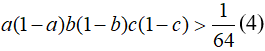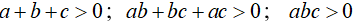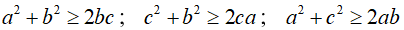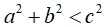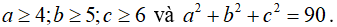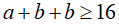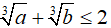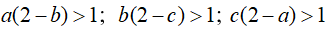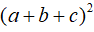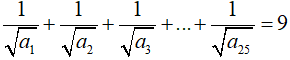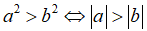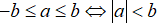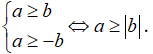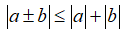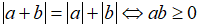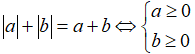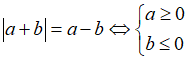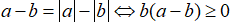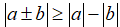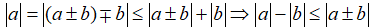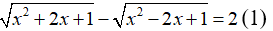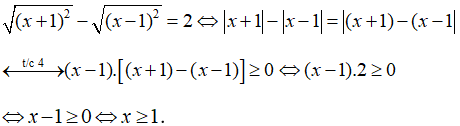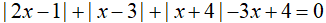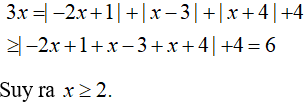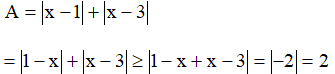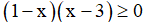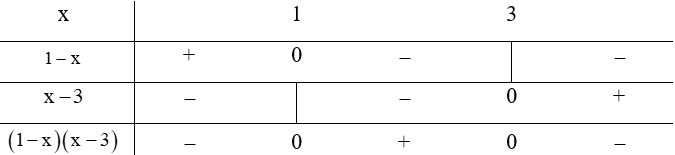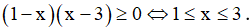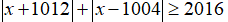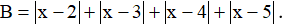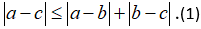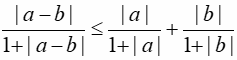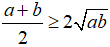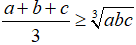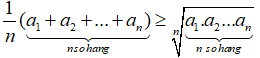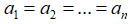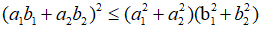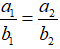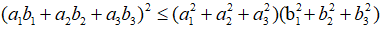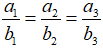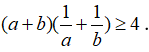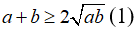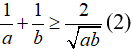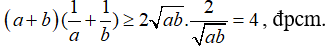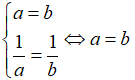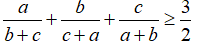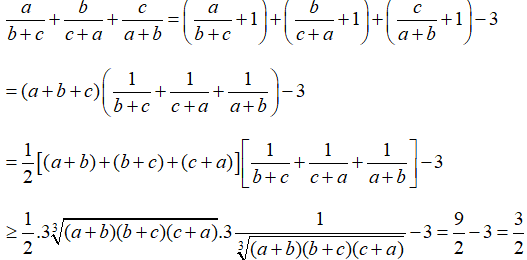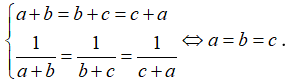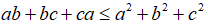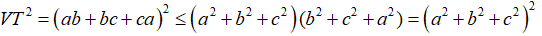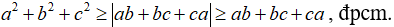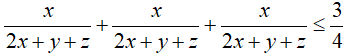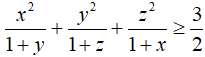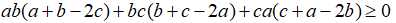Tổng hợp các cách chứng minh bất đẳng thức hay, chi tiết
Tổng hợp các cách chứng minh bất đẳng thức hay, chi tiết
Tài liệu Tổng hợp các cách chứng minh bất đẳng thức hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
Dạng 1: Sử dụng biến đổi tương đương
A. Phương pháp giải
Một số kĩ thuật cơ bản:
+ Kỹ thuật xét hiệu hai biểu thức
+ Kỹ thuật sử dụng các hằng đẳng thức
+ Kỹ thuật thêm bớt một hằng số, một biểu thức
+ Kỹ thuật đặt biến phụ
+ Kỹ thuật sắp thứ tự các biến.
+ Kỹ thuật khai thác tính bị chặn của các biến
B. Ví dụ minh họa
Câu 1: Cho a và b là hai số bất kỳ chứng minh rằng
Lời giải:
Câu 2:
Lời giải:
Áp dụng:
Ta viết bất đẳng thức
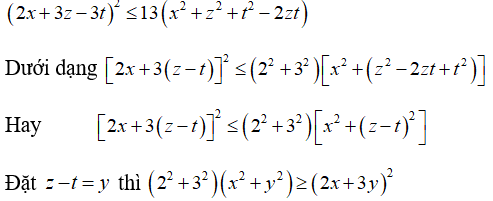
đúng theo bất đẳng thức vừa chứng minh ở trên.
Câu 3: Chứng minh rằng với ba số a,b,c tùy ý ta luôn có:
Lời giải:
Xét hiệu:
C. Bài tập tự luyện
Câu 1: Cho a, b, c là các số thực bất kì. Chứng minh rằng:
Câu 2: Cho a, b, c là các số thực bất kì. Chứng minh rằng:
Câu 3: Cho a, b, c, d, e là các số thực bất kì. Chứng minh rằng:
Câu 4: Cho a, b, c là các số thực thỏa mãn điều kiện a, b, c ≥1. Chứng minh rằng:
Câu 5: Cho a, b, c là các số thực dương thỏa mãn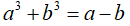 
.
Chứng minh rằng: 
Câu 6: Cho các số thực a, b, c thỏa mãn điều kiện a+b+c=0 .
Chứng minh rằng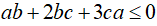 
.
Câu 7: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:
Câu 8: Chứng minh rằng với mọi số thực khác không a, b ta có:
Dạng 2: Sử dụng phương pháp phản chứng
A. Phương pháp giải
+ Dùng mệnh đề đảo
+ Phủ định rồi suy ra điều trái với giả thiết
+ Phủ định rồi suy ra trái với điều đúng
+ Phủ định rồi suy ra hai mệnh đề trái ngược nhau
+ Phủ định rồi suy ra kết luận
*Một số đẳng thức và bất đẳng thức cần nhớ:
B. Ví dụ minh họa
Câu 1: Chứng minh rằng: 
Lời giải:
Điều này là vô lý với mọi a và b
Vậy điều giả sử là sai →điều phải chứng minh.
Câu 2: Cho ba số a, b, c ∈ (0;1) . Chứng minh rằng có ít nhất một trong các bất đẳng thức sau đây là sai:
Lời giải:
Giả sử cả ba bất đẳng thức trên đều đúng. Theo giả thiết a, b, c, 1-a, 1-b, 1-c đều là số dương suy ra
Mặt khác:
Câu 3: Cho a, b, c là các số thực thỏa mãn các điều kiện sau:
Chứng minh rằng cả ba số a, b, c đều là số dương.
Lời giải:
Giả sử rằng trong ba số a, b, c có một số không dương, không mất tổng quát ta chọn số đó là a, tức là a≤0.
Vì abc>0 nên a≠0, do đó suy ra a<0.
C. Bài tập tự luyện
Câu 1: Cho a, b, c là các số thực bất kì. Chứng minh rằng có ít nhất một trong các bất đẳng thức sau đây là đúng:
Câu 2: Cho a, b, c là các số thực thỏa mãn điều kiện
.
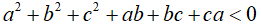
Chứng minh rằng:
Câu 3: Cho a, b, c là các số thực thỏa mãn
Chứng minh rằng:
Câu 4: Cho a, b là các số thực dương thỏa mãn a+b=2. Chứng minh rằng:
Câu 5: Cho các số thực a, b, c ∈ (0;2). Chứng minh rằng có ít nhất một trong ba bất đẳng thức sau đây là sai:
Câu 6: Cho ba số thực a, b, c đôi một khác nhau. Chứng minh rằng tồn tại ít nhất một trong các số 9ab, 9bc, 9ac nhỏ hơn 
Câu 7: Cho 25 số tự nhiên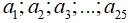 
khác 0 thỏa mãn điều kiện:
Dạng 3: Sử dụng bất đẳng thức về giá trị tuyệt đối
A. Phương pháp giải
Ta có các tính chất sau :
Tính chất 1: Với hai số thực a, b tùy ý:
Tính chất 2: Ta có:
Tính chất 3: Ta có:
Tính chất 4: Ta có:
*Với phương trình ta sử dụng các tính chất:
Tính chất 1: Nếu:
Tính chất 2: Nếu:
Tính chất 3: Nếu:
Tính chất 4: Nếu:
B. Ví dụ minh họa
Câu 1: Chứng minh rằng với mọi số thực a, b ta luôn có:
Lời giải:
Ta có:
Câu 2: Giải phương trình:
Lời giải:
Ta biến đổi phương trình về dạng:
Vậy, phương trình có nghiệm là x≥1.
Câu 3: Cho số thực x thỏa mãn 
Chứng minh rằng x≥2
Lời giải:
Ta có:
Câu 4: a) Tìm giá trị nhỏ nhất của biểu thức: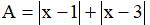 
.
b) Tìm tất cả các giá trị của x để đạt được giá trị nhỏ nhất đó.
Lời giải:
a) Áp dụng bất đẳng thức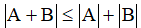 
ta có
Dễ thấy khi x = 1 thì A = 2. Vậy giá trị nhỏ nhất của biểu thức A là 2
b) Theo nhận xét trên, dấu "=" ở bất đẳng thức trên xảy ra khi và chỉ khi
Ta có bảng xét dấu:
Dựa vào bảng ta có 
C. Bài tập tự luyện
Câu 1: Chứng minh rằng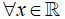 
:
Câu 2: Tìm tất cả các số nguyên x để biểu thức sau đây đạt giá trị nhỏ nhất:
Câu 3: Chứng minh rằng với mọi số thực a, b, c ta luôn có:
Câu 4:
a) Chứng minh rằng với mọi số thực a, b ta có |a ± b| ≥ |a| - |b|.
b) Biết rằng | a | > 2 | b |. Chứng minh rằng |a| < 2|a - b|.
Câu 5: Chứng minh rằng:
a. Nếu x ≥ y ≥ 0 thì
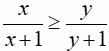
b. Với hai số a, b tuỳ ý, ta có
Dạng 4: Sử dụng bất đẳng thức Cô – si, bất đẳng thức Bunhiacopxki
A. Phương pháp giải
a) Bất đẳng thức Cô – si
Cho hai số không âm a, b, ta luôn có:
, dấu đẳng thức xảy ra khi và chỉ khi a=b.
Mở rộng:
a. Với các số a, b, c không âm, ta luôn có:
Dấu đẳng thức xảy ra khi và chỉ khi a=b=c.
b. Với n số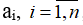 
không âm, ta luôn có:
Dấu đẳng thức xảy ra khi và chỉ khi 
b) Bất đẳng thức Bunhiacopxki
Cho a1, a2, b1, b2 là những số thực, ta có:
Dấu đẳng thức xảy ra khi
Mở rộng: Với các số thực a1, a2, b1, b2, a3, b3, ta luôn có:
Dấu đẳng thức xảy ra khi
B. Ví dụ minh họa
Câu 1: Cho a,b>0. Chứng minh rằng:
Lời giải:
Sử dụng bất đẳng thức Cô-si:
- Cho cặp số a, b, ta được:
- Cho cặp số
, ta được:
Nhân hai vế tương ứng của (1), (2), ta được:
Dấu bằng xảy ra khi:
Câu 2: Cho ba số dương a, b, c. Chứng minh rằng:
Giải.
Ta có:
Dấu đẳng thức xảy ra khi:
Câu 3: Chứng minh rằng với a, b, c tùy ý ta luôn có:
Lời giải:
Ta có:
Lấy căn bậc hai của hai vế, ta đi đến:
C. Bài tập tự luyện
Câu 1: Cho 3 số dương x, y, z tùy ý. Chứng minh rằng:
Câu 2: Cho 3 số dương x, y, z thỏa mãn: xyz=1. Chứng minh rằng:
Câu 3: Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng:
Câu 4: Cho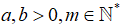 
. Chứng minh rằng:
Câu 5: Chứng minh rằng với mọi số thực x, y luôn có:
Câu 6: Hai số x, y thỏa mãn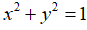 
. Chứng minh rằng
Câu 7: Cho các số không âm a, y thỏa mãn 
. Chứng minh rằng:
