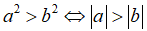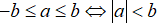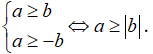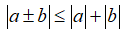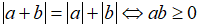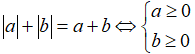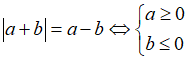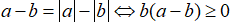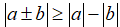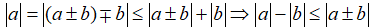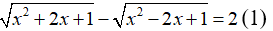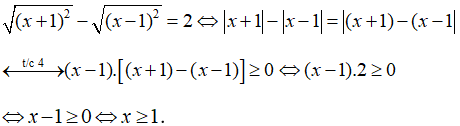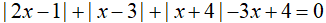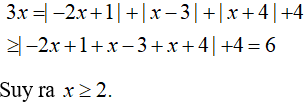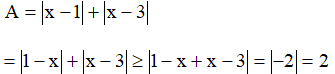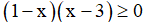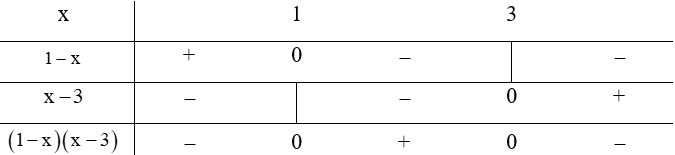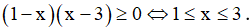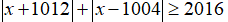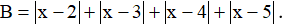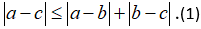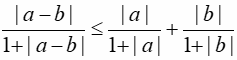Chứng minh bất đẳng thức bằng giá trị tuyệt đối
Chứng minh bất đẳng thức bằng giá trị tuyệt đối
Tài liệu Chứng minh bất đẳng thức bằng giá trị tuyệt đối Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
Dạng bài: Sử dụng bất đẳng thức về giá trị tuyệt đối
A. Phương pháp giải
Ta có các tính chất sau :
Tính chất 1: Với hai số thực a, b tùy ý:
Tính chất 2: Ta có:
Tính chất 3: Ta có:
Tính chất 4: Ta có:
*Với phương trình ta sử dụng các tính chất:
Tính chất 1: Nếu:
Tính chất 2: Nếu:
Tính chất 3: Nếu:
Tính chất 4: Nếu:
B. Ví dụ minh họa
Câu 1: Chứng minh rằng với mọi số thực a, b ta luôn có:
Lời giải:
Ta có:
Câu 2: Giải phương trình:
Lời giải:
Ta biến đổi phương trình về dạng:
Vậy, phương trình có nghiệm là x≥1.
Câu 3: Cho số thực x thỏa mãn 
Chứng minh rằng x≥2
Lời giải:
Ta có:
Câu 4: a) Tìm giá trị nhỏ nhất của biểu thức: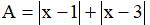 
.
b) Tìm tất cả các giá trị của x để đạt được giá trị nhỏ nhất đó.
Lời giải:
a) Áp dụng bất đẳng thức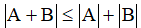 
ta có
Dễ thấy khi x = 1 thì A = 2. Vậy giá trị nhỏ nhất của biểu thức A là 2
b) Theo nhận xét trên, dấu "=" ở bất đẳng thức trên xảy ra khi và chỉ khi
Ta có bảng xét dấu:
Dựa vào bảng ta có 
C. Bài tập tự luyện
Câu 1: Chứng minh rằng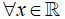 
:
Câu 2: Tìm tất cả các số nguyên x để biểu thức sau đây đạt giá trị nhỏ nhất:
Câu 3: Chứng minh rằng với mọi số thực a, b, c ta luôn có:
Câu 4:
a) Chứng minh rằng với mọi số thực a, b ta có |a ± b| ≥ |a| - |b|.
b) Biết rằng | a | > 2 | b |. Chứng minh rằng |a| < 2|a - b|.
Câu 5: Chứng minh rằng:
a. Nếu x ≥ y ≥ 0 thì
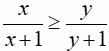
b. Với hai số a, b tuỳ ý, ta có
