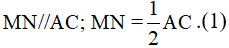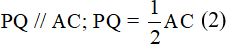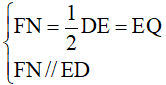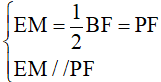Cách chứng minh tứ giác là hình bình hành hay, chi tiết
Cách chứng minh tứ giác là hình bình hành hay, chi tiết
Tài liệu Cách chứng minh tứ giác là hình bình hành hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải
Nhận dạng hình bình hành: Thường sử dụng dấu hiệu nhận biết về cạnh đối và đường chéo.
- Tứ giác có các cạnh đối song song là hình bình hành
- Tứ giác có các cạnh đối bằng nhau là hình bình hành
- Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành
- Tứ giác có các góc đối bằng nhau là hình bình hành
- Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
B. Ví dụ minh họa
Ví dụ 1. Tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác MNPQ là hình gì? Vì sao?
Giải
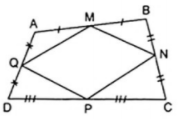
Tứ giác MNPQ là hình bình hành.
Giải thích: Thật vậy, từ giả thiết ta có MQ, NP thứ tự là các đường trung
bình của hai tam giác ABD và BCD. Áp dụng định lí đường trung bình vào hai tam giác đó, ta được:
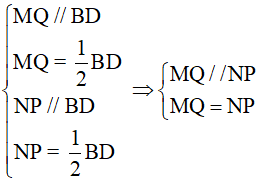
Tứ giác MNPQ có hai cạnh đối song song và bằng nhau nên nó là hình bình hành.
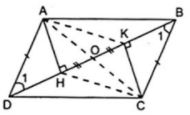
Ví dụ 2. Cho hình sau, trong đó ABCD là hình bình hành. Chứng minh tứ giác AHCK là hình bình hành.
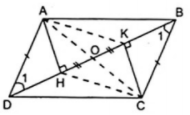
Giải
Từ giả thiết
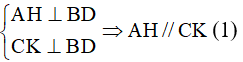
Áp dụng tính chất về cạnh vào hình bình hành ABCD và tính chất góc so le của AD//BC ta được:
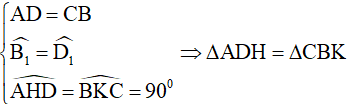
(trường hợp cạnh huyền, góc nhọn).
Suy ra AH = CK. (2)
Từ (1) và (2) ta có tứ giác AHCK có hai cạnh đối song song và bằng nhau nên nó là hình bình hành.
Ví dụ 3. Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở E, tia phân giác của góc C cắt AB ở F. Chứng minh rằng: Tứ giác AFCE là hình bình hành.
Giải
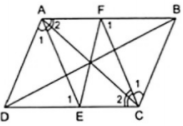
Áp dụng định nghĩa vào hình bình hành ABCD, ta được AB//DC, suy ra AE//EC. (1)
Áp dụng tính chất về góc, giả thiết vào hình bình hành ABCD và tính chất của các cặp góc so le, ta được:
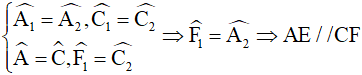
(vì có cặp góc đồng vị bằng nhau). (2)
Từ (1) và (2) ta có tứ giác AFCE có các cạnh đối song song nên nó là hình bình hành.
C. Bài tập vận dụng
Câu 1. Hãy chọn câu sai:
A. Tứ giác có hai cặp cạnh đối song song là hình bình hành.
B. Hình thang có hai góc kề một đáy bằng nhau là hình bình hành.
C. Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành.
D. Tứ giác có hai cặp góc đối bằng nhau là hình bình hành.
Câu 2. Hãy chọn câu đúng. Tứ giác ABCD là hình bình hành nếu.
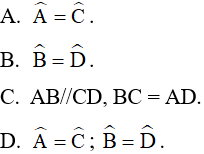
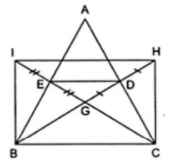
Câu 3. Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G. M và N lần lượt là trung điểm của GC và GB. Tứ giác MNED là hình gì?
A. Hình chữ nhật.
B. Hình bình hành.
C. Hình thang cân.
D. Hình thang vuông.
Câu 4. Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G. Vẽ các điểm H, I sao cho D là trung điểm của GH, E là trung điểm của GI. Tứ giác BIHC là hình gì?
A. Hình bình hành.
B. Hình thang
C. Hình thang cân
D. Cả A, B, C đều sai
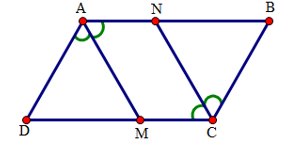
Câu 5. Hãy chọn câu đúng. Cho hình bình hành ABCD có các điều kiện như hình vẽ, trong hình có:
A. 6 hình bình hành.
B. 5 hình bình hành.
C. 4 hình bình hành.
D. 3 hình bình hành.
Câu 6. Hãy chọn câu trả lời sai.
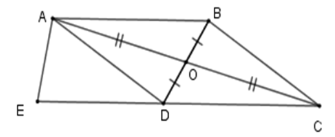
Cho hình vẽ, ta có:
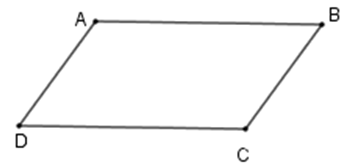
A. ABCD là hình bình hành.
B. AB//DC.
C. ABCD là hình thang cân.
D. BC//AD.
Câu 7. Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD tại M. Tia phân giác góc C cắt AB tại N (hình vẽ). Hãy chọn câu trả lời sai.
A. AMCN là hình bình hành.
B. CMAB là hình thang.
C. ANCD là hình thang cân.
D. AN = MC.
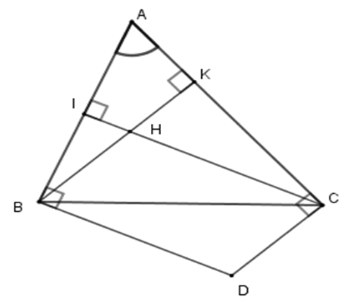
Câu 8. Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D.
Chọn câu trả lời đúng nhất. Tứ giác BDCH là hình gì?
A. Hình thang
B. Hình bình hành
C. Hình thang cân
D. Hình thang vuông
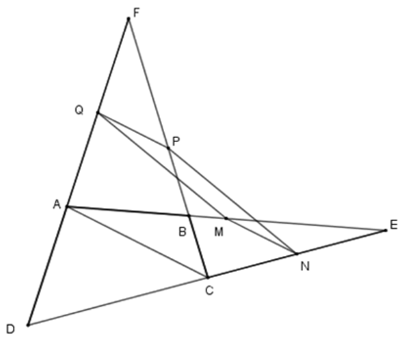
Câu 9. Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD, AD và BC; M, N, P, Q lần lượt là trung điểm của AE, EC, CF, FA. Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất.
A. Hình bình hành.
B. Hình thang vuông.
C. Hình thang cân.
D. Hình thang.
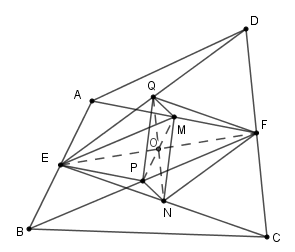
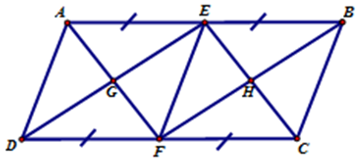
Câu 10. Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB và CD. M, N, P, Q lần lượt là trung điểm của AF, CE, BF, DE. Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất.
A. Hình bình hành.
B. Hình thang vuông.
C. Hình thang cân.
D. Hình thang.

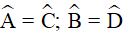 nên D đúng.
nên D đúng.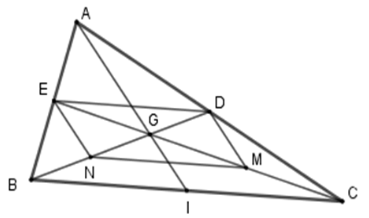
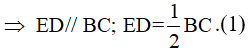
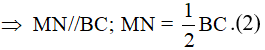
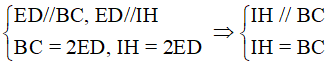

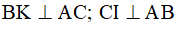 hay
hay 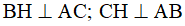 (vì H là trực tâm).
(vì H là trực tâm).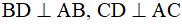 (giả thiết) nên BD//CH (cùng vuông với AB) và CD//BH (cùng vuông với AC). Suy ra tứ giác BHCD là hình bình hành.
(giả thiết) nên BD//CH (cùng vuông với AB) và CD//BH (cùng vuông với AC). Suy ra tứ giác BHCD là hình bình hành.