Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán hình học, vật lí, hóa học
Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán hình học, vật lí, hóa học
Tài liệu Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán hình học, vật lí, hóa học Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
A. Phương pháp giải
• Các bước giải bài toán bằng cách lập phương trình:
Bước 1: Lập phương trình
- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
- Biểu diễn các đại lượng chưa biết khác theo ẩn và các đại lượng đã biết.
- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Trả lời
Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không rồi kết luận.
• Công thức tính chu vi, diên tích các hình (tích hợp hình học)
Chu vi hình chữ nhật C = 2(a + b) [2*(chiều dài + chiều rộng)]
Diện tích hình chữ nhật S = a.b (chiều dài * chiều rộng)
Chu vi hình vuông: C = 4a (a là độ dài cạnh)
Diện tích hình vuông: S = a2 (a là độ dài cạnh)
Diện tích hình bình hành: S = a.h (chiều cao*cạnh tương ứng)
• Công thức tính nhiệt lượng: Q = m.c. Δt
• Phương trình cân bằng nhiệt Qtỏa = Qthu (tích hợp vật lí)
• Định luật bảo toàn khối lượng: Trong một phản ứng hóa học, tổng khối lượng các chất sản phẩm bằng tổng khối lượng các chất tham gia phản ứng (tích hợp hóa học)
B. Ví dụ minh họa
Ví dụ 1: Chu vi một khu vườn hình chữ nhật bằng 60m, hiệu độ dài của chiều dài và chiều rộng là 20m. Tìm độ dài các cạnh của hình chữ nhật.
Hướng dẫn giải:
Gọi chiều dài của khu vườn là x (m) (20 < x < 30)
Chiều rộng của khu vườn là x – 20 (m)
Chu vi của khu vườn bằng 60m nên ta có phương trình:
(x + x – 20). 2 = 60 ⇔ 2x – 20 = 30 ⇔ 2x = 50 ⇔ x = 25 (tmđk)
Vậy chiều dài của mảnh vườn là 25m, chiều rộng là 25 - 20 = 5m.
Ví dụ 2: Người ta pha 3kg nước nóng ở 90°C với 2kg nước lạnh ở 20°C. Tính nhiệt độ sau cùng của nước (bỏ qua sự mất nhiệt)
Hướng dẫn giải:
Gọi nhiệt độ sau cùng của nước là x°C (20 < x < 90)
Áp dụng công thức tính nhiệt lượng Q = m.c. Δt ta có:
Nhiệt lượng 3kg nước nóng tỏa ra đến khi cân bằng nhiệt là Qtỏa = 3.4200(90 – x)
Nhiệt lượng 2kg nước lạnh thu vào đến khi cân bằng nhiệt là Qthu = 2.4200(x - 20)
Theo phương trình cân bằng nhiệt Qtỏa = Qthu nên ta có phương trình:
3.4200(90 – x) = 2.4200(x - 20)
⇔ 3(90 – x) = 2(x – 20)
⇔ 270 – 3x = 2x – 40 ⇔ 5x = 310
⇔ x = 62 (tmđk)
Vậy nhiệt độ sau cùng của nước là 62°C
Ví dụ 3: Có hai loại dung dịch muối I và II. Người ta hòa 200 gam dung dịch muối I với 300gam dung dịch muối II thì được một dung dịch có nồng độ muối là 33%. Tính nồng độ muối trong mỗi dung dịch I và II, biết rằng nồng độ muối trong dung dịch I lớn hơn nồng độ muối trong dung dịch II là 20%.
Hướng dẫn giải:
Gọi nồng độ muối trong dung dịch I là x (%)(x > 20), nồng độ muối trong dung dịch II là x – 20(%)
Lượng muối có trong dung dịch I là 200.x%,
lượng muối có trong dung dịch II là 300.(x -20)%.
Theo định luật bảo toàn khối lượng ta có khối lượng dung dịch tạo thành là 200 + 300 = 500g
Theo bài ra ta có phương trình:
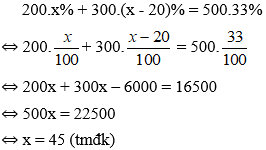
Vậy nồng độ mưới của dung dịch I là 45%, nồng độ muối của dung dịch II là 25%
C. Bài tập vận dụng
Bài 1: Một hình chữ nhật có chu vi 320m. Nếu tăng chiều dài 10m, tăng chiều rộng 20m thì diện tích tăng 2700m2. Tính chiều dài và chiều rộng của hình.
Hướng dẫn giải:
Gọi chiều rộng hình chũ nhật là x (m)(0 < x < 160)
Nửa chu vi hình chữ nhật là: 320:2 = 160 m
Chiều dài là 160 - x (m)
Diện tích của hình chữ nhật là: x (160 – x) (m2)
Khi tăng chiều dài thêm 10m và chiều rộng thêm 20m thì diện tích của hình là:
(x + 20)(160 – x + 10) = (x + 20)(170 – x)
Vì diện tích tăng 2700m2 nên ta có phương trình:
x (160 – x) + 2700 = (x + 20)(170 – x)
⇔ 160x –x2 + 2700 = 150x – x2 + 3400
⇔ 10x = 700 ⇔ x = 70 (tmđk)
Vậy hình chữ nhật có chiều rộng là 70m, chiều dài là 160 – x = 90m
Bài 2: Một thửa đất hình chữ nhật có chu vi là 56m. Nếu giảm chiều rộng 2m và tăng chiều dài 4m thì diện tích tăng thêm 8m2. Tìm chiều rộng và chiều dài thửa đất.
Hướng dẫn giải:
Gọi chiều rộng của thửa đất là x (m) (x > 2)
Nửa chu vi của thửa đất là: 56:2 = 28(m)
Chiều dài của thửa đất là 28 – x (m)
Diện tích của thửa đất là x(28 – x) (m2)
Khi tăng chiều dài lên 4m, giảm chiều rộng đi 2m ta có diện tích là
(x – 2)(28 – x + 4) = (x – 2)(32 – x) (m2)
Khi đó diện tích tăng thêm 8m2 nên ta có phương trình.
x(28 – x) + 8 = (x – 2)(32 – x))
⇔ 28x – x2 + 8 = 34x – x2 – 64
⇔ 6x = 72 ⇔ x = 12 (tmđk)
Vậy chiều rộng của thửa đất là 12m, chiều dài thửa đất là 28 – 12 = 16m.
Bài 3: Một khu vườn hình chữ nhật có chiều dài bằng 3 lần chiều rộng. Nếu tăng mỗi cạnh thêm 5m thì diện tích khu vườn tăng thêm 385m2. Tính độ dài các cạnh của khu vườn.
Hướng dẫn giải:
Gọi chiều rộng của mảnh vườn là x (m) (x > 0)
Chiều dài của mảnh vườn là 3x (m)
Diện tích mảnh vườn là 3x.x = 3x2
Khi tăng mỗi cạnh lên 5m thì diện tích mảnh vườn là: (3x + 5)(x + 5) = 3x2 + 20x + 25.
Khi đó diện tích tăng thêm 385m2 nên ta có phương trình:
3x2 + 385 = 3x2 + 20x +25 ⇔ 20x = 360 ⇔ x = 18(tmđk)
Vậy chiều rộng của mảnh vườn là 18m, chiều dài của mảnh vườn là 18.3 = 54m
Bài 4: Hiệu số đo chu vi của hai hình vuông là 32m và hiệu số đo diện tích của chúng là 464m2. Tìm số đo các cạnh của mỗi hình vuông.
Hướng dẫn giải:
Gọi độ dài cạnh của hình vuông nhỏ là x (m) (x > 0)
Chu vi hình vuông nhỏ là 4x (m)
Chu vi hình vuông lớn là 4x + 32
Độ dài cạnh hình vuông lớn là (4x + 32): 4 = 4(x + 8): 4 = x + 8 (m)
Diện tích hình vuông nhỏ là x2 (m2)
Diện tích hình vuông lớn là (x + 8)2
Theo bài ra ta có phương trình:
(x + 8)2 – x2 = 464
⇔ x2 + 16x + 64 – x2 = 464
⇔ 16x = 400 ⇔ x = 25 (tmđk)
Vậy cạnh hình vuông nhỏ là 25m; cạnh hình vuông lớn là 25 + 8 = 33m.
Bài 5: Một khu vườn hình chữ nhật có chu vi là 450m. Nếu giảm chiều dài đi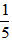 
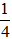
chiều dài cũ và tăng chiều rộng thêm 
chiều rộng cũ thì chu vi hình chữ nhật không đổi. Tính chiều dài và chiều rộng khu vườn.
Hướng dẫn giải:
Gọi chiều rộng của khu vườn là x (m) (x > 0)
Nửa chu vi của hình chữ nhật là: 450 : 2 = 225 m
Chiều dài của khu vườn là 225 – x (m)
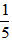
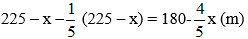
Khi giảm chiều dài đi chiều dài cũ ta được chiều dài mới là:
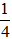
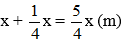
Khi tăng chiều rộng thêm chiều rộng cũ thì ta được chiều rộng mới là 
Khi đó chu vi hình chữ nhật không đổi nghĩa là ta có phương trình:
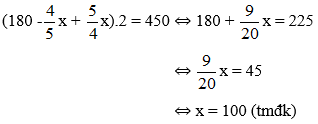
Vậy chiều rộng của khu vườn là 100m, chiều dài của khu vườn là 125m.
Bài 6: Một khu đất hình chữ nhật có chiều dài hơn chiều rộng là 10m. Nếu chiều dài tăng thêm 6m, chiều rộng giảm đi 3m thì diện tích mới tăng hơn diện tích cũ là 12m2. Tính các kích thước của khu đất.
Hướng dẫn giải:
Gọi chiều rộng của khu đất là x (m) (x > 3)
Chiều dài của khu đất là x + 10 (m)
Diện tích của khu đất là x(x + 10) (m2)
Khi tăng chiều dài thêm 6m thì chiều dài của khu đất là x + 10 + 6 = x + 16 (m)
Khi giảm chiều rộng đi 3m thì chiều rộng của khu đất là x - 3 (m)
Diện tích của khu đất lúc này là (x – 3)(x + 16)
Vì diện tích mới tăng hơn diện tích cũ là 12m2 nên ta có phương trình:
(x – 3)(x + 16) = x(x + 10) + 12
⇔ x2 + 13x – 48 = x2 + 10x + 12
⇔ 3x = 60
⇔ x = 20 (tm đk)
Vậy chiều rộng của khu đất là 20 m, chiều dài của khu đất là 20 + 10 = 30m
Bài 7: Hai cạnh của một hình bình hành có độ dài là 6cm và 8cm. Đường cao ứng với cạnh 6cm có độ dài là 5cm. Tính độ dài đường cao thứ hai?
Hướng dẫn giải:
Gọi x (cm) là độ dài đường cao thứ hai ứng với cạnh 8cm của hình bình hành (0 < x < 5)
Theo công thức tính diện tích hình bình hành ta có phương trình:
6.5 = 8.x ⇔ 8x =30 ⇔ x = 3,75 (tmđk)
Vậy độ dài đường cao thứ hai là 3,75cm
Bài 8: Một hình thang có diện tích 160cm2, đường cao bằng 8cm. tính độ dài mỗi đáy hình thang biết hai đáy hơn kém nhau 10cm.
Hướng dẫn giải:
Gọi chiều dài đáy nhỏ của hình thang là x (cm) (x > 0)
Chiều dài đáy lớn là x + 10 (cm)
Diện tích hình thang là 160cm2
Theo công thức tính diện tích hình thang ta có phương trình: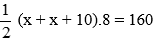 
Giải phương trình:
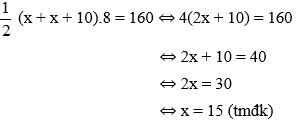
Vậy chiều dài đáy nhỏ của hình thang là 15cm, chiều dài đáy lớn của hình thang là 25cm.
Bài 9: Một mảnh đất hình chữ nhật có chiều dài hơn chiều rộng 6m, và bình phương độ dài đường chéo gấp 5 lần chu vi. Xác định chiều dài và chiều rộng mảnh đất?
Hướng dẫn giải:
Gọi chiều dài mảnh đất là x (m)(x > 6)
Chiều rộng mảnh đất là x – 6 (m)
Chu vi mảnh đất là 2(x + x – 6) = 4x – 12 (m)
Theo định lí Py-ta-go ta có bình phương đường chéo của mảnh đất là x2 + (x – 6)2
Vì bình phương đường chéo gấp 5 lần chu vi nên ta có phương trình:
x2 + (x – 6)2 = 5(4x – 12)
⇔ x2 + x2 – 12x + 36 = 20x – 60
⇔ 2x2 – 32x + 96 = 0
⇔ x2 – 16x + 48 = 0
⇔ (x – 12)(x – 4) = 0 ⇔ x = 12 (tmđk) hoặc x = 4 (không tmđk x > 6)
Vậy chiều dài của mảnh đất là 12m, chiều rộng của mảnh đất là 6m
Bài 10: Một tam giác vuông có hai cạnh góc vuông hơn kém nhau 8m, nếu tăng độ dài cạnh góc vuông nhỏ lên 2 lần và giảm độ dài cạnh góc vuông còn lại xuống 3 lần thì được tam giác vuông mới có diện tích bằng 51m2.Tính độ dài hai cạnh góc vuông?
Hướng dẫn giải:
Gọi độ dài cạnh góc vuông nhỏ là x (m)(x > 0)
Độ dài cạnh góc vuông lớn là x + 8 (m)
Khi tăng độ dài cạnh góc vuông nhỏ lên 2 lần ta được cạnh có độ dài 2x (m)
Khi giảm độ dài cạnh góc vuông còn lại xuống 3 lần thì được cạnh có độ dài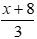 
(m)
Tam giác vuông mới có diện tích bằng 51m2
Theo công thức tính diện tích tam giác vuông ta có phương trình:
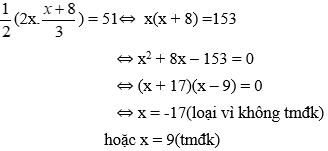
Vậy độ dài cạnh góc vuông nhỏ là 9m. Độ dài cạnh góc vuông lớn là 17m.
