Chứng minh hai đường thẳng vuông góc dựa vào hình vuông

Chứng minh hai đường thẳng vuông góc dựa vào hình vuông

Tài liệu Chứng minh hai đường thẳng vuông góc dựa vào hình vuông Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải

Sử dụng định nghĩa và các tính chất của hình vuông

• Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.
• Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.
• Đường chéo của hình vuông vừa bằng nhau vừa vuông góc với nhau.
• Ví dụ minh họa

Ví dụ 1. Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, trên cạnh CD lấy điểm N sao cho BM = CN. Chứng minh rằng .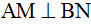

Giải

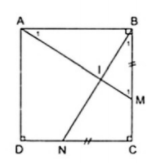
Áp dụng định nghĩa và giả thiết vào hình vuông ABCD ta được:

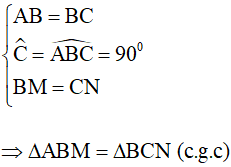
Gọi I là giao điểm của AM và BN.

Áp dụng tính chất về góc vào tam giác vuông ABM và BCN, kết quả của hai tam giác bằng nhau, ta được:

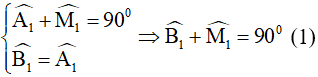
Áp dụng tính chất về góc vào tam giác BIM ta có

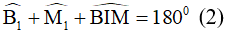
Từ (1) và (2) suy ra 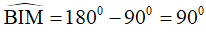hay .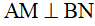

Ví dụ 2. Cho hình vuông ABCD. Trên tia đối của tia CB lấy điểm M, trên tia đối của tia DC lấy điểm N sao cho BM = DN. Vẽ hình bình hành MANF, gọi O là trung điểm của AF. Chứng minh rằng .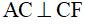

Giải

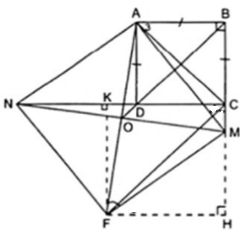
Xét hai tam giác ABM vuông tại B và AND vuông tại D có:

AB = AD (ABCD là hình vuông)

BM = DN (gt)

Suy ra 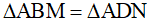(cạnh góc vuông – cạnh góc vuông)

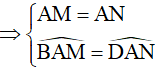
Hình bình hành MANF có hai cạnh kề AM và AN bằng nhau nên là hình thoi.

Do góc MAD phụ với góc MAB nên góc MAD phụ với DAN hay .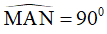

Điều này chứng tỏ hình thoi MANF là hình vuông vì hình thoi có một góc vuông.

Kẻ FH, FK theo thứ tự vuông góc với hai đường thẳng BC, NC thu được tứ giác KCHF có ba góc vuông nên là hình chữ nhật, suy ra .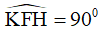

Lại có 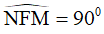vì là góc của hình vuông nên 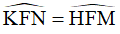do cùng phụ với .

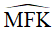Xét tam giác FKN vuông tại K và FHM vuông tại H có:

NF = MF (MANF là hình vuông)

Điều này chứng tỏ F cách đều hai cạnh CM, CN của góc MCN nên F thuộc tia phân giác của góc MCN.

Kết hợp với tính chất về đường chéo của hình vuông ta có:

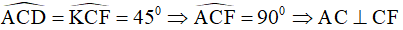
Ví dụ 3. Cho hình vuông ABCD. Trên cạnh BC lấy M bất kì. Trên cạnh AD lấy N sao cho AM = AN. Kẻ 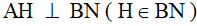, AH cắt CD tại E. Tính số đo .

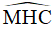Giải

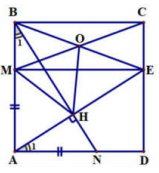
Hai tam giác vuông ABN và DAE có:

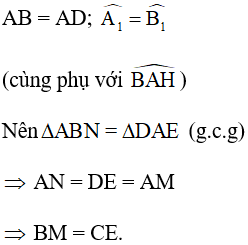
Xét tứ giác BMEC có BM//CE, BM = CE, 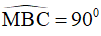. Do đó BMEC là hình chữ nhật.

Gọi O là giao điểm hai đường chéo BE và CM, ta có OB = OE = OC = OM.

Mặt khác ta có tam giác BHE vuông tại H có HO là trung tuyến

⇒OH = OB = OE (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)

⇒OH = OC = OM

⇒ΔMHC vuông tại H hay .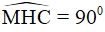

Ví dụ 4. Cho hình vuông ABCD. Gọi O là giao điểm hai đường chéo AC và BD. Vẽ tia phân giác của 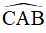cắt đường chéo BD tại E và cạnh BC tại F. Vẽ 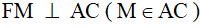. Chứng minh rằng .

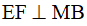Giải

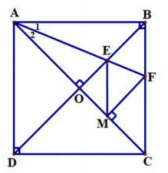
Xét hai tam giác vuông AMF và ABF có:

Do ABCD là hình vuông nên đường chéo BD là đường phân giác của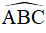

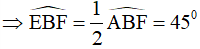
AC là đường phân giác của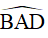

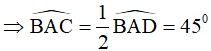
AF là phân giác của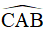

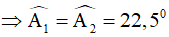
Xét tam giác ABF có

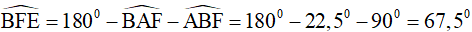
Xét tam giác BAE có góc ngoài đỉnh E là

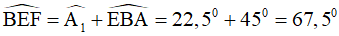
Vậy tam giác BEF cân tại B ⇒ BE = BF. (2)

Tương tự ta chứng minh được ME = MF. (3)

Từ (1), (2) và (3) suy ra tứ giác BEMF là hình thoi.

Áp dụng tính chất đường chéo của hình thoi ta được 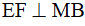.