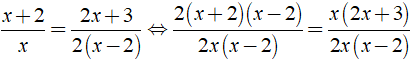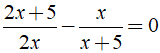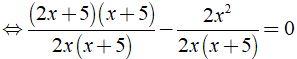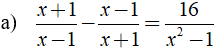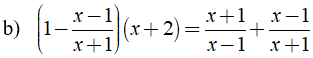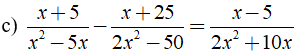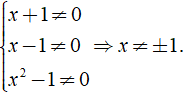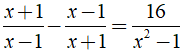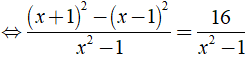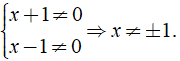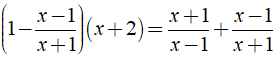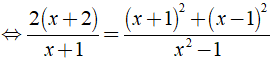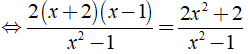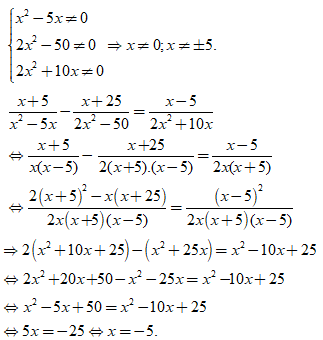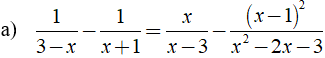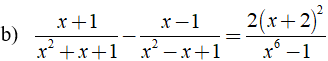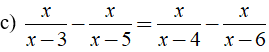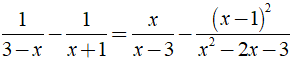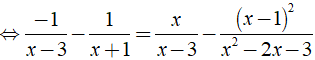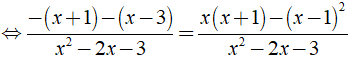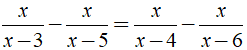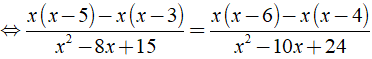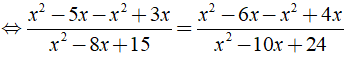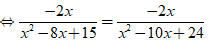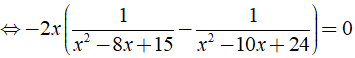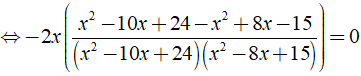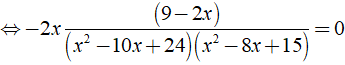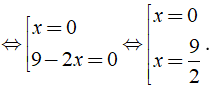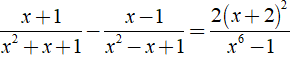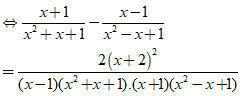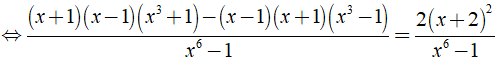Lý thuyết Phương trình chứa ẩn ở mẫu hay, chi tiết

Lý thuyết Phương trình chứa ẩn ở mẫu hay, chi tiết

Haylamdo biên soạn và sưu tầm Lý thuyết Phương trình chứa ẩn ở mẫu hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Lý thuyết

1. Tìm điều kiện xác định của một phương trình

Điều kiện xác định của phương trình là tập hợp các giá trị của ẩn làm cho tất cả các mẫu trong phương trình đều khác 0.

Điều kiện xác định của phương trình viết tắt là ĐKXĐ.

Ví dụ: Tìm điều kiện xác định của các phương trình sau

a) (x - 1)/(x + 2) + 1 = 1/(x - 2).

b) (x - 1)/(1 - 2x) = 1.

Hướng dẫn:

a) Ta thấy x + 2 ≠ 0 khi x ≠ - 2 và x - 2 ≠ 0 khi x ≠ 2.

Do đó ĐKXĐ của phương trình (x - 1)/(x + 2) + 1 = 1/(x - 2) là x ≠ ± 2.

b) Ta thấy 1 - 2x ≠ 0 khi x ≠ 1/2.

Do đó ĐKXĐ của phương trình (x - 1)/(1 - 2x) = 1 là x ≠ 1/2.

2. Giải phương trình chứa ẩn ở mẫu

Ta thường qua các bước:

Bước 1: Tìm điều kiện xác định của phương trình

Bước 2: Quy đồng mẫu hai vế rồi khử mẫu.

Bước 3: Giải phương trình tìm được.

Bước 4: Kết luận.

Nghiệm của phương trình là giá trị của ẩn thoả mãn ĐKXĐ của phương trình.

Ví dụ 1: Giải phương trình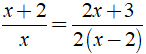

Hướng dẫn:

Bước 1: Điều kiện xác định: x ≠ 0; x ≠ 2.

Bước 2: Quy đồng mẫu hai vế rồi khử mẫu

Ta có:

⇒ 2( x - 2 )( x + 2 ) = x( 2x + 3 )

Bước 3: Giải phương trình

Ta có: 2( x - 2 )( x + 2 ) = x( 2x + 3 ) ⇔ 2( x² - 4 ) = 2x² + 3x

⇔ 2x² - 8 = 2x² + 3x ⇔ 3x = - 8 ⇔ x = - 8/3.

Bước 4: Kết luận

So sánh với ĐKXĐ, ta thấy x = - 8/3 thỏa mãn.

Vậy phương trình đã cho có tập nghiệm S = { - 8/3 }.

Ví dụ 2: Giải phương trình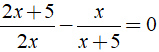

Hướng dẫn:

+ ĐKXĐ: x ≠ 0; x ≠ - 5.

+ Ta có:

⇒ ( 2x + 5 )( x + 5 ) - 2x² = 0

⇔ 2x² + 10x + 5x + 25 - 2x² = 0 ⇔ 15x = - 25 ⇔ x = - 5/3.

+ So sánh với ĐKXĐ ta thấy x = - 5/3 thỏa mãn điều kiện.

Vậy phương trình đã cho có tập nghiệm là S = { - 5/3 }.

B. Bài tập tự luyện

Bài 1: Giải các phương trình sau:

Hướng dẫn:

a) ĐKXĐ:

Ta có:

⇒ (x + 1)² - (x - 1)² = 16

⇔ ( x² + 2x + 1 ) - ( x² - 2x + 1 ) = 16

⇔ 4x = 16 ⇔ x = 4.

Vây phương trình đã cho có nghiệm x = 4.

b) ĐKXĐ:

Ta có:

⇒ 2( x² + x - 2 ) = 2x² + 2

⇔ 2x² + 2x - 4 = 2x² + 2

⇔ 2x = 6 ⇔ x = 3.

Vậy phương trình đã cho có nghiệm là x = 3.

c) ĐKXĐ:

Bài 2: Giải các phương trình sau:

Hướng dẫn:

a) ĐKXĐ: x ≠ - 1;x ≠ 3.

Ta có:

⇒ - x - 1 - x + 3 = x² + x - x² + 2x - 1

⇔ -2x + 2 = 3x - 1

⇔ 5x = 3 ⇔ x = 3/5.

Kết hợp điều kiện, vậy phương trình đã cho có nghiệm là x = 3/5.

b) ĐKXĐ: x ≠ 3, x ≠ 4, x ≠ 5, x ≠ 6.

Ta có:

Vậy phương trình đã cho có nghiệm là x = 0;x = 9/2.

c) ĐKXĐ: x ≠ 1 hoặc x = -1.

Ta có:

⇒ ( x² - 1 )( x³ + 1 ) - ( x² - 1 )( x³ - 1 ) = 2( x² + 4x + 4 )

= 2(x² + 4x + 4)

⇔ ( x⁵ + x² - x³ - 1 ) - ( x⁵ - x² - x³ + 1 ) = 2( x² + 4x + 4 )

⇔ 2x² - 2 = 2x² + 8x + 8

⇔ 8x = - 10 ⇔ x = - 5/4.

Vậy phương trình đã cho có nghiệm là x = - 5/4.