Tính số mặt, số đỉnh, số cạnh của hình chóp đều
Tính số mặt, số đỉnh, số cạnh của hình chóp đều
Tài liệu Tính số mặt, số đỉnh, số cạnh của hình chóp đều Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Tính số mặt, số đỉnh, số cạnh của hình chóp đều
A. Phương pháp giải
+) Trước hết số cạnh của mặt đáy rồi suy ra số mặt, số đỉnh, số cạnh của hình chóp đều theo công thức dưới đây:
Số cạnh của một đáy |
Số mặt |
Số đỉnh |
Số cạnh |
n |
n+1 |
n+1 |
2n |
B. Ví dụ minh họa
Câu 1: Hình chóp tứ giác đều có mặt bên là hình gì?
A. Tam giác cân
B. Tam giác đều
C. Tam giác vuông
D. Tam giác vuông cân
Lời giải:
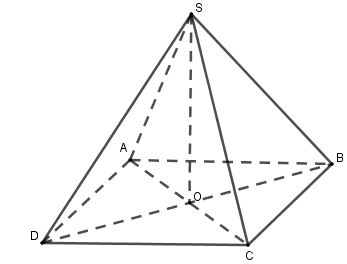
Hình chóp tứ giác đều có các cạnh bên bằng nhau và các cạnh đáy bằng nhau nên mặt bên là những tam giác cân.
Câu 2: Hình chóp lục giác đều có bao nhiêu mặt?
A. 4 |
B. 5 |
C. 6 |
D. 7 |
Lời giải:
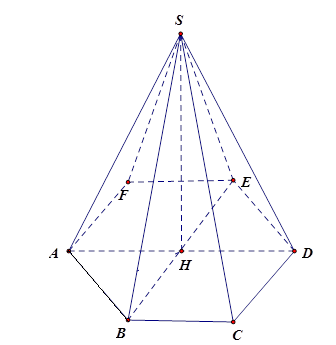
Hình lục giác đều có 6 mặt bên và 1 mặt đáy nên có tất cả 7 mặt.
Câu 3: Quan sát các hình dưới đây và điền cụm từ và số thích hợp vào ô trống, biết các hình dưới đây là hình chóp đều
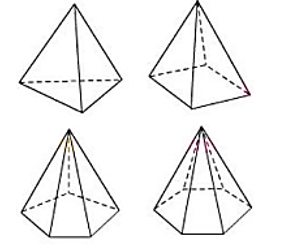
Chóp tam giác đều |
Chóp tứ giác đều |
Chóp ngũ giác đều |
Chóp lục giác đều |
|
Đáy |
Tam giác đều |
|||
Mặt bên |
Tam giác cân |
|||
Số cạnh đáy |
5 |
|||
Số cạnh |
10 |
|||
Số mặt |
5 |
Lời giải:
Chóp tam giác đều |
Chóp tứ giác đều |
Chóp ngũ giác đều |
Chóp lục giác đều |
|
Đáy |
Tam giác đều |
Hình vuông |
Ngũ giác đều |
Lục giác đều |
Mặt bên |
Tam giác đều |
Tam giác cân |
Tam giác cân |
Tam giác cân |
Số cạnh đáy |
3 |
4 |
5 |
6 |
Số cạnh |
6 |
8 |
10 |
12 |
Số mặt |
4 |
5 |
6 |
7 |
C. Bài tập tự luyện
Câu 1:Mặt bên của hình chóp cụt đều là hình gì?
A. Hình chữ nhật
B. Hình vuông
C. Hình thang cân
D. Tứ giác bất kì
Câu 2: Hình chóp tam giác đều có đáy là?
A. Tam giác cân
B. Tam giác đều
C. Tam giác vuông
D. Hình vuông
Câu 3: Hình chóp lục giác đều có bao nhiêu cạnh?
A. 6 |
B. 7 |
C. 10 |
D. 12 |
Câu 4: Cho một hình chóp lục giác đều. Hỏi nó có bao nhiêu mặt, bao nhiêu đỉnh và bao nhiêu cạnh?
Câu 5: Một hình chóp đều có tổng số mặt và số đỉnh là 12. Tính số cạnh của đa giác đáy.
Câu 6: Gọi M là số mặt, D là số đỉnh và C là số cạnh của hình chóp đều. Chứng minh rằng M+D-C=2.

